一致性哈希算法（一）- 问题的提出

• 一致性哈希算法是一种特殊的哈希算法， 当目标槽位数量发生变化时，它会尽力降低的重新映射的数量。
• 传统的哈希表设计中，添加或者删除一个槽位，会造成全量的重新映射， 一致性哈希则追求的是增量式重新映射。
• 一致性哈希最早由Karger在1997年提出，多用于分布式系统中的扩容缩容问题、 分布式哈希表的设计等等。

本文是第一部分， 将从一个kvdb的设计谈起，解答「为什么需要一致性哈希」的问题。

如何代理一个简单的kvdb？

假如我们有一个简单的kvdb (key-value-database)， 它支持两个简单的操作：

• set(k,v)：表示把键为 k 的值更新为 v。
• get(k)→v：表示查询键为 k 的值为 v。

由于单节点系统的服务能力有限， 因此我们要考虑多节点的架构方案。 一种简单的架构方案是：前面做一个代理服务，把请求分割到不同的后端节点上， 这是常说的sharding模式。

下面的图1.1是这个kvdb的架构图，

• 蓝色的节点是一个代理服务器， 负责为到来的读写请求分配一个后端节点。
• 后面的紫色的节点都是存储节点。

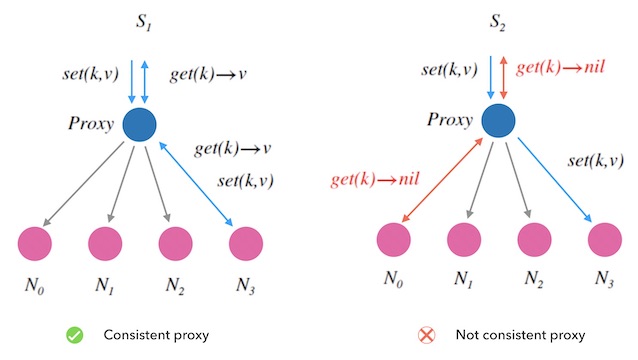
图1.1 - sharding模式水平扩容kvdb

可以看到左边的 S1 总会给同一个 k 分配不变的后端节点， 而右边的 S2 则不然， 它先给 set(k,v) 分配了 N3, 又为后续的 get(k) 分配了 N0 ， 导致 get 读取失败， 所以 S2 是无法正确地工作的。 我们称 S1 的代理方式是有一致性的， S2 的则没有。

我们将寻找一种有一致性的代理方案：

对同一个 key 的所有读写请求都必须一致地分配给同一个后端节点。 同时，分配的负载应该尽量均衡。

换句话讲， 我们需要寻找一种映射函数， 把随机到来的字符串 key ，一致地映射到 n 个槽中。 此外，我们也希望，这个映射要做到尽量平均。

简单的哈希映射 - Mod-N哈希

哈希表是一种常用的基本数据结构。

例如下面图2.1，它把随机到来的字符串 k 输入到哈希函数 hash 中， 然后映射到一张连续内存表上。

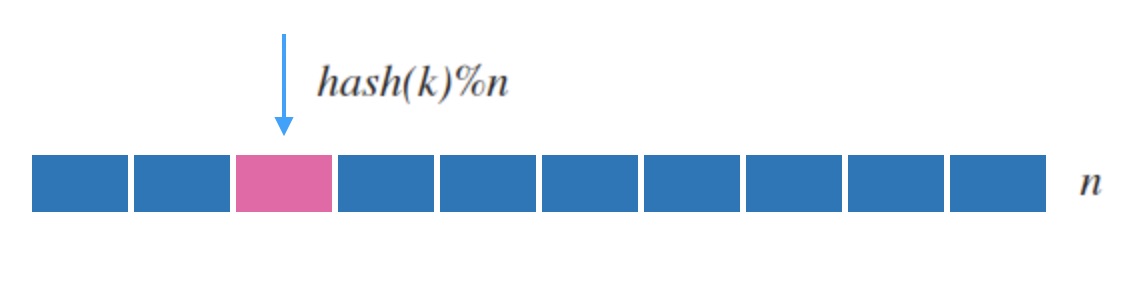
图2.1 - 哈希表的映射示意

一般地，常见的哈希函数(如 md5, sha1)都是映射到uint32这样很大的空间的， 所以哈希表一般对哈希函数的结果取余数来映射到槽位， 即 hash(k)%n 。 因为 hash 函数本身保证了映射的分布平均 和 一致性， 所以求余后的结果也符合我们的要求。

如下面图2.2， 我们可以用类似哈希表的方式来作为kvdb的节点分配规则：

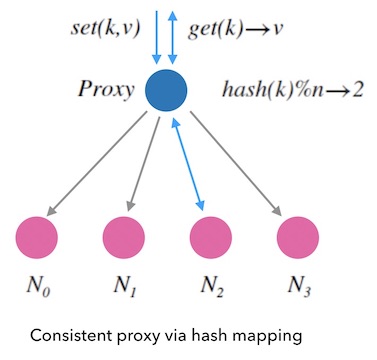
图2.2 - 哈希映射的方式实现一致性代理

我们先把这种映射方式叫做「Mod-N哈希法」。

还记得哈希表的扩容吗？ 当哈希表中插入元素越来越多的时候，哈希表就需要扩容。 这时候不得不重新申请一块新的连续内存，把所有的元素拷贝过去并进行重新映射(rehash)。

哈希表的扩容和重新映射都是全量进行的。 如果kvdb也模仿这种方式进行扩容， 就需要全量迁移数据，显然太麻烦了， 我们要寻找增量扩容的方式。

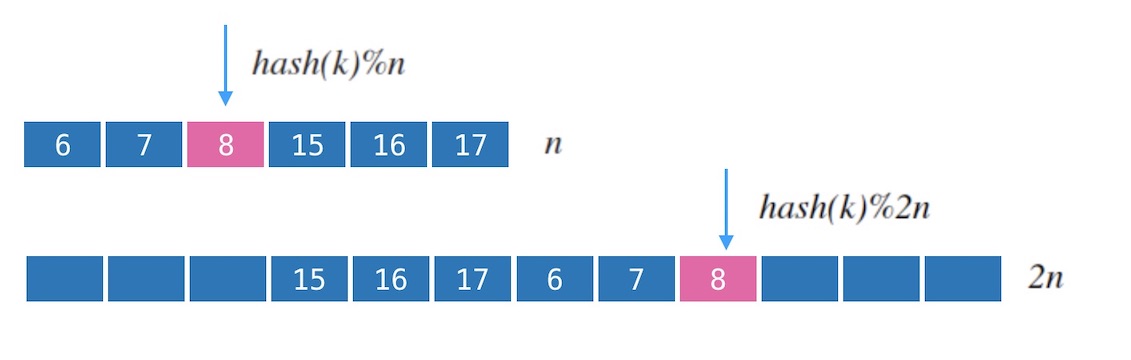
图2.3 - 哈希表的扩容和重新映射

Mod-N哈希的扩容问题

下面，我们看下在前面提到的Mod-N哈希法的情况下， 新加一个节点或者移除一个故障节点会发生什么。

下图3.1中， 当新加一个节点 N4 时， 我们看到原本分配到 N2 的 k 在扩容后会分配到 N1。 对于一个kvdb来说，这意味着我们需要在扩容后把 k 从 N2 迁移到 N1 才能继续提供服务。 否则的话，扩容后的读请求将映射到新的节点 N1， 而导致读不到数据。

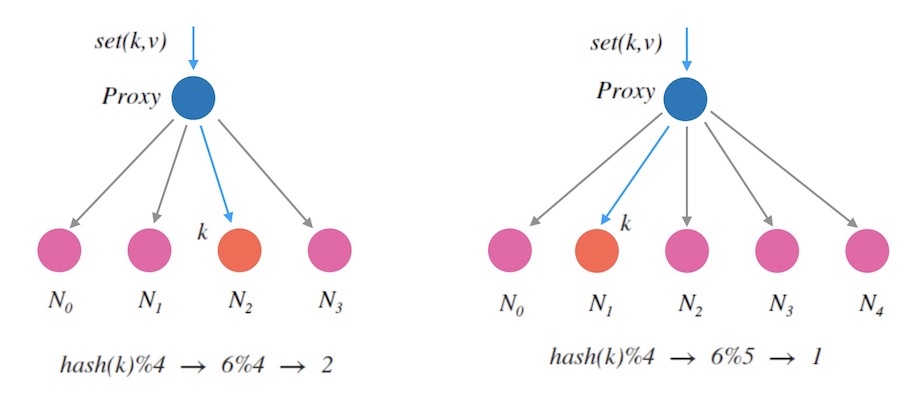
图3.1 - 新加一个节点的情况

图3.1指出了，新增一个节点，会导致新映射和老映射的不一致。

对于删除一个节点的情况，也是类似的， 同样会导致新映射和老映射的不一致。 从下面图3.2中可以看到， 原本映射到 N2 的 k 在缩容后映射到了 N0， 也是不一致的：

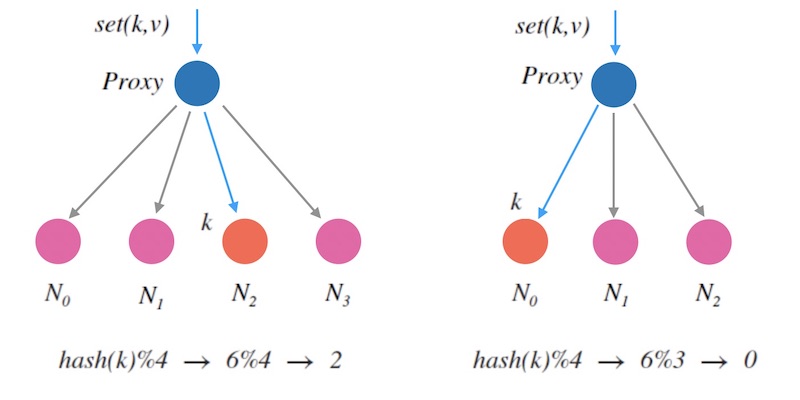
图3.2 - 删除一个节点的情况

这种情况并不是特例， 而是会导致大面积的映射不一致。

下面的图3.3是4个节点和5个节点的情况下的哈希映射的对比图， 图中数字表示 hash(k) 的值， 红色标记的数字则代表两种情况下的没有映射到同一个节点的值。 可以确定的是， 节点数变更后会导致大面积的映射不一致。

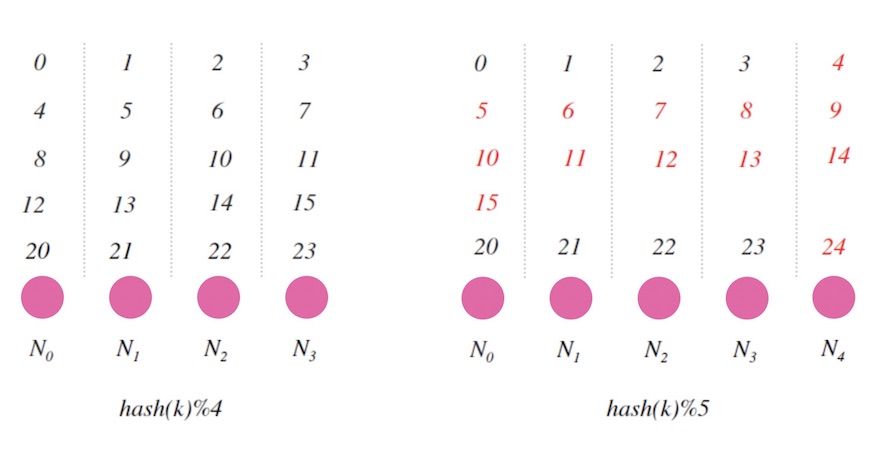
图3.3 - 4个节点和5个节点的情况下的哈希映射对比

其实从数学上也可以简单地推出来， 只有当 hash(k) 的结果对 4 和 5 的余数相等时才可能一致， 比如图中的 0,1,2,3,20,21,22,23，…， 其他情况都会不一致。

这样，我们对要寻找的映射函数的一致性要求更高了， 不仅要求对相同的 k 的多次映射结果一致， 还要尽可能减少 n 变化时带来的不一致性映射的变化。 构造这种映射的算法，就是一致性哈希算法。

一致性哈希算法

我们希望构造一种函数 f(k,n)→m 把字符串映射到 n 个槽上：

• 它的输入是随机到来的字符串 k 和 槽的个数 n.
• 输出是映射到的槽的标号 m , m<n.

这个函数需要有这样的性质：

• 映射均匀： 对随机到来的输入 k， 函数返回任一个 m 的概率都应该是 1/n 。

• 一致性：

  • 相同的 k, n 输入， 一定会有相同的输出。
  • 当槽的数目增减时， 映射结果和之前不一致的字符串的数量要尽量少。

  更严格的、维基百科的定义是： 当添加一个槽时， 只需要对 K/n 个字符串进行进行重新映射。

这个算法的关键特征在于， 不要导致全局重新映射， 而是要做增量的重新映射。

接下来将介绍三种一致性哈希算法：

• 哈希环法
• 跳跃一致性哈希法
• Maglev一致性哈希法

一致性哈希算法（二）- 哈希环法

哈希环法是最常用的、最经典的一致性哈希算法， 也叫做割环法。 这个算法易于理解、应用广泛（例如亚马逊的Dynamo）， 实现了最小化的重新映射。

一致性哈希环算法

具体的算法：

1. 设 hash(key) 是映射到区间 [0,2^32]上的一个哈希函数。 把区间首尾相连，形成一个顺时针增长的哈希环（如图5.1） 。
2. 将所有槽位(或者节点) N0,..,n−1 的标号 0,…,n−1依次作为 hash 函数的输入进行哈希，把结果分别标记在环上。
3. 对于关于 k 的映射，求出 z=hash(k) ， 标记在环上：
   1. 如果 z 正好落在槽位上，返回这个槽位的标号。
   2. 否则， 顺时针沿着环寻找离 z 最近的槽位，返回槽位标号。

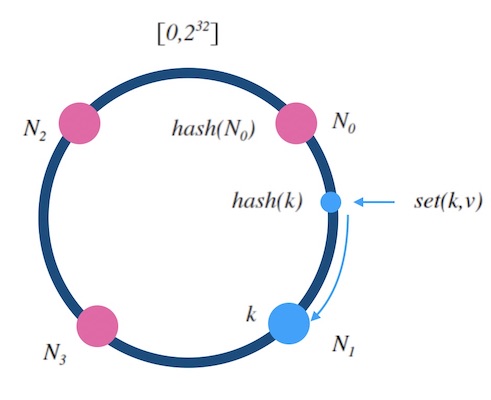
图5.1 - 哈希环示意图

我们接下来讨论下， 当新增和删除槽位时， 哈希环的表现如何。

当往一个哈希环中新增一个槽位时，如下图5.2中， 红色的 N4 是新增的槽位。 可以看到 k 从 N1 重新映射到了 N4 , 而 k1 的映射结果不变。 稍加分析可以知道， 只有被新增槽位拦下来的 k 的映射结果是变化了的。 新增槽位拦截了原本到下一节点的部分映射，其他槽位不受影响。 对于kvdb的例子 来说， 顺时针方向的下一个节点 N1 需要迁移部分数据到新节点 N4 上才可以正常服务， 其他节点不受影响。

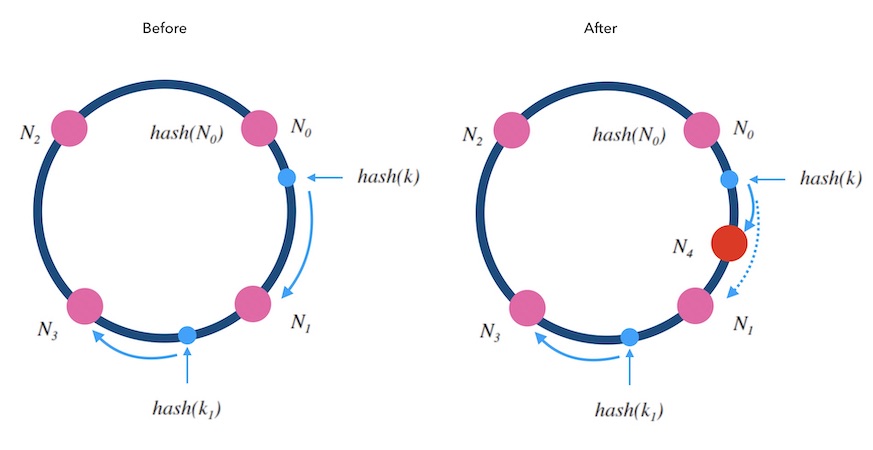
图5.2 - 向哈希环新增一个槽位

当从一个哈希环中移除一个槽位时， 如下图5.3中， 红色的 N1 是被删除的槽位。 可以看到 k 从 N1 重新映射到了 N3， 而 k1 的映射结果不变。 被删除槽位的映射会转交给下一槽位，其他槽位不受影响。 对于kvdb的例子来说， 顺时针方向的原本映射到 N1 的请求会被 转交到顺时针方向的下一个节点 N3 处理， 所以需要迁移 N1 的数据到 N3 才可以正常服务， 下一个节点 N1 需要迁移部分数据到新节点 N4 上才可以正常服务， 其他节点不受影响。

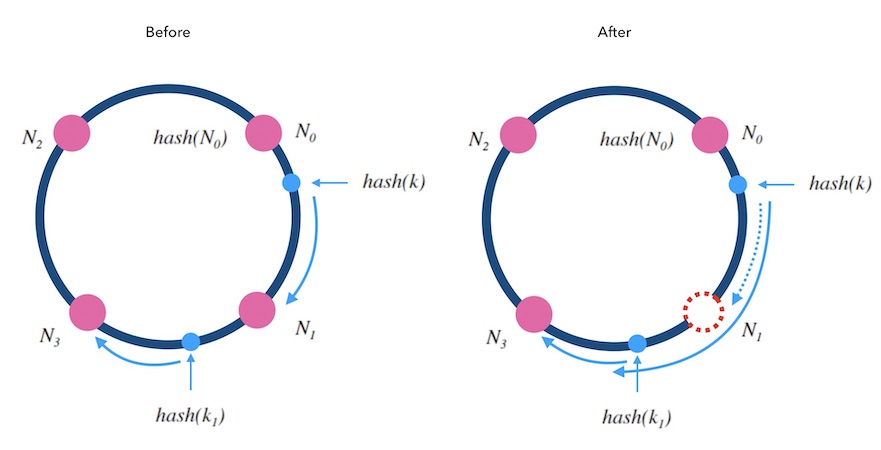
图5.3 - 从哈希环中删除一个槽位

哈希环做到了在槽位数量变化前后的增量式的重新映射， 避免了全量的重新映射。

假设整体的 k 的数量是 K , 由于哈希映射的均匀性， 所以，添加或者删除一个槽位，总会只影响一个槽位的映射量，也就是 1/K , 因此，哈希环做到了最小化重新映射(minimum disruption)，做到了完全的一致性。

哈希环法的复杂度分析

在技术实现上，实现哈希环的方法一般叫做 ketama 或 hash ring。 核心的逻辑在于如何在环上找一个和目标值 z 相近的槽位， 我们把环拉开成一个自然数轴， 所有的槽位在环上的哈希值组成一个有序表。 在有序表里做查找， 这是**二分查找**可以解决的事情， 所以哈希环的映射函数的时间复杂度是 O(logn)。

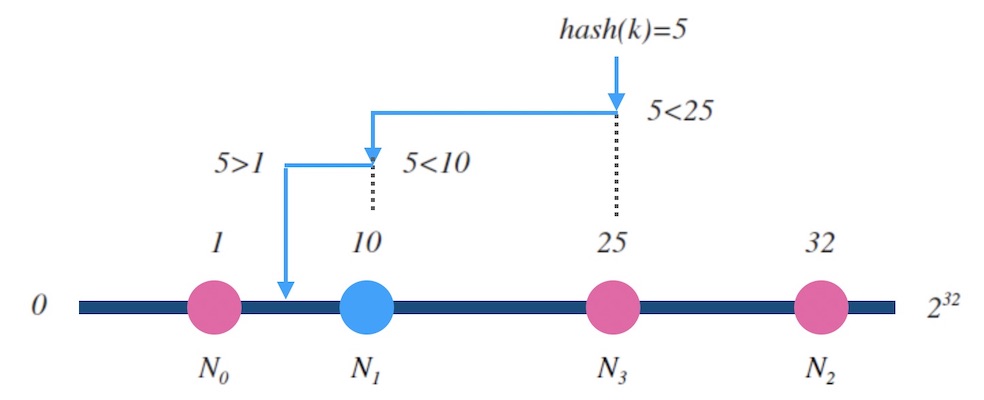
图6.1 - 哈希环上二分查找

*附注: 我对ketama做了简单的实现： C语言版本， Go语言版本*。

对于空间复杂度，显然是 O(n)。

带权重的一致性哈希环

实际应用中， 还可以对槽位（节点）添加权重。 大概的逻辑是构建很多指向真实节点的虚拟节点， 也叫影子节点。 影子节点之间是平权的，选中影子节点，就代表选中了背后的真实节点。 权重越大的节点，影子节点越多， 被选中的概率就越大。

下面的图6.2是一个例子， 其中 N0,N1,N2,N3 的权重比是 1:2:3:2。 选中一个影子节点如 V(N2) 就是选中了 N2 。

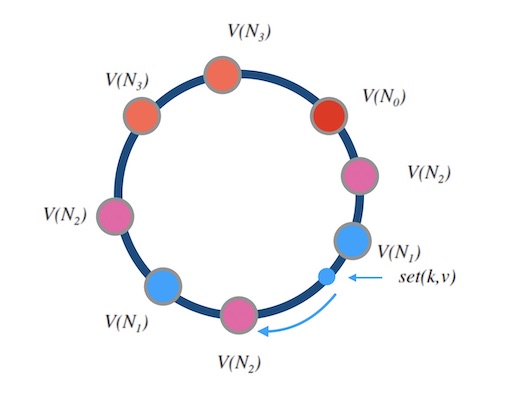
图6.2 - 加权哈希环

但是需要注意的是， 权重的调整会带来数据迁移的工作。

哈希环上的映射分布的均匀性

实际应用中，即使节点之间是平权的， 也会采用影子节点。 比如，常用的ketama方法中，一般采用一个节点对应40个影子节点。 原因是，节点越多、映射的分布越均匀， 采用影子节点可以减少真实节点之间的负载差异。

一致性哈希环算法的映射结果仍然不是很均匀[1]：

With 100 replicas (“vnodes”) per server, the standard deviation of load is about 10%. Increasing the number of replicas to 1000 points per server reduces the standard deviation to ~3.2%.

意思是， 当有100个影子节点时，哈希环法的映射结果的分布的标准差大约有 10%。 当影子节点增加到1000个时，这个标准差降到 3.2% 左右。

另外，和下一篇文章讨论的跳跃一致性哈希算法的均匀性对比， 哈希环的表现也不是很好。

影子节点是一个绝妙的设计，不仅提高了映射结果的均匀性， 而且为实现加权映射提供了方式。 但是，影子节点增加了内存消耗和查找时间， 以常用的ketama为例， 每个节点都对应40个影子节点， 内存的消耗从 O(n) 变为 O(40n) ， 查找时间从 O(logn) 变为 O(log(40n)) 。

一致性哈希环下的热扩容和容灾

回到kvdb的例子上来， 对于增删节点的情况，哈希环法做到了增量式的重新映射， 不再需要全量数据迁移的工作。 但仍然有部分数据出现了变更前后映射不一致， 技术运营上仍然存在如下问题：

• 扩容：当增加节点时，新节点需要对齐下一节点的数据后才可以正常服务。
• 缩容：当删除节点时，需要先把数据备份到下一节点才可以停服移除。
• 故障：节点突然故障不得不移除时，面临数据丢失风险。

如果我们要实现动态扩容和缩容，即所谓的热扩容，不停止服务对系统进行增删节点， 可以这样做：

1. **数据备份(双写)**： 数据写入到某个节点时，同时写一个备份(replica)到顺时针的邻居节点。
2. **请求中继(代理)**： 新节点刚加入后，数据没有同步完成时，对读取不到的数据，可以把请求中继(replay)到顺时针方向的邻居节点。

下面的图7.1中演示了这两种规则：

1. 移除节点的情况： 每一个节点在执行写请求时，都会写一个备份到顺时针的邻居节点。 这样，当 N3 节点因故障需要踢除时，新的请求会交接给它的邻居节点 N2， N2 上有 k1 的备份数据，可以正常读到。

2. 新增节点的情况： 对于新增节点的情况稍微复杂点， 当新增节点 N4 时， N4 需要从邻居节点 N1 上同步数据， 在同步仍未完成时，可能遇到的请求查不到数据， 此时可以先把请求中继给 N1 处理, 待两个节点数据对齐后，再结束中继机制。

   就像细胞分裂一样， N4 刚加入时可以直接算作时 N3 的一部分， N3 算作一个大节点， 当数据对齐后， N4 再从 N3 中分裂出来，正式成为新节点。

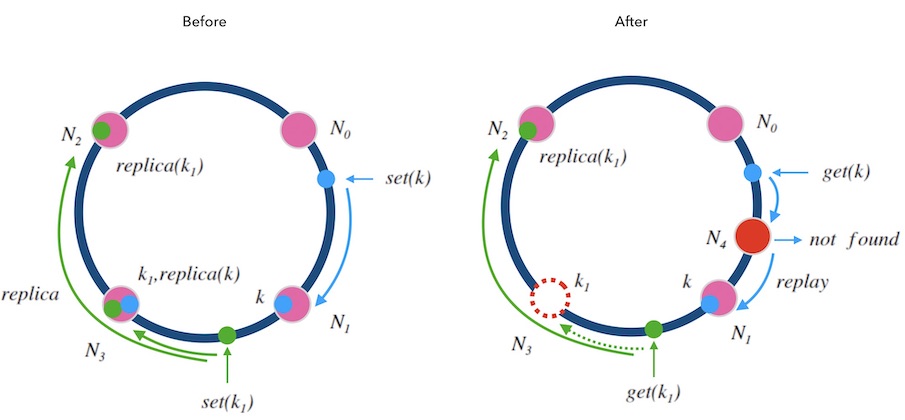
图7.1 - 带备份和中继的哈希环

另外， 可以备份不止一份。 下面图7.2中演示了备份两次情况， 每个写请求都将备份同步到顺时针方向的最近的两个节点上。 这样就可以容忍相邻的两节点损失的情况， 进一步提高了系统的可用性。

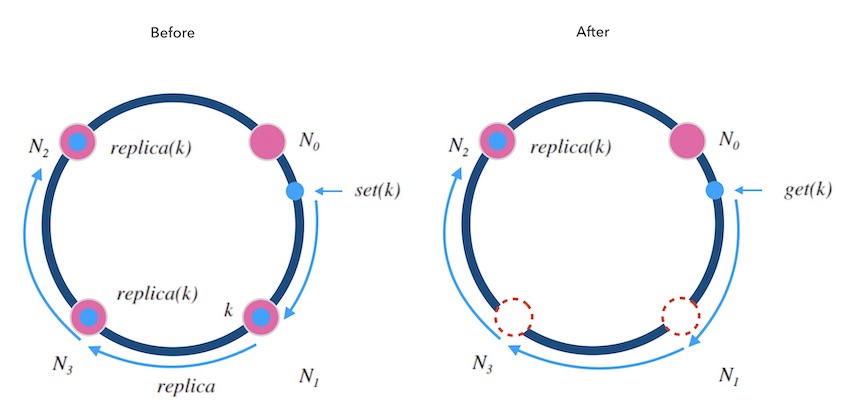
图7.2 - 备份两次的情况

同样的，中继也可以不止一次。 下面图7.3中演示了中继两次的情况， 如果一个节点上查不到数据，就中继给下一个节点，最多两次中继， 这样就可以满足同时添加”两个正好在环上相邻的”节点的情况了。

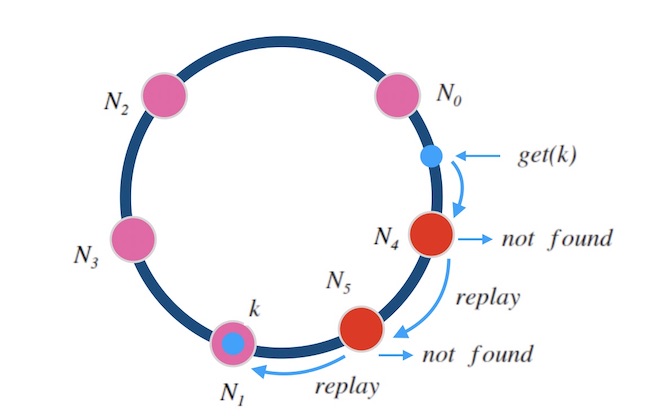图7.3 - 中继两次的情况

小结

哈希环法是经典的一致性哈希算法， 避免了因槽位数量变化导致的全量重新映射， 实现了最小化的重新映射。 时间复杂度是 O(log(n))， 空间复杂度是 O(n)， 实际根据影子节点数量而乘上相应倍数。 映射均匀性不是很优秀。 热扩容和容灾的方式比较直观。

一致性哈希算法（三）- 跳跃一致性哈希法

跳跃一致性哈希法

跳跃一致性哈希 ( Jump Consistent Hash ) 是 Google 于2014年发布的一个极简的、快速的一致性哈希算法[1]。 这个算法精简到可以用几行代码来描述， 下面的就是 Google 原论文中的算法的 C++ 表示：

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
  int64_t b = -1, j = 0;
  while (j < num_buckets) {
    b = j;
    key = key * 2862933555777941757ULL + 1;
    j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
  }
  return b;
}

函数 JumpConsistentHash 是一个一致性哈希函数， 它把一个 key 一致性地映射到给定几个槽位中的一个上， 输入 key 和槽位数量 num_buckets， 输出映射到的槽位标号。

这个函数虽然短，却不那么容易看懂。 现在，先不要纠结上面这个函数本身， 我们一步一步地看论文中是如何推导出来这个函数的。

跳跃一致性哈希法的推导

假设，我们要求的一致性哈希函数是 ch(k,n)， n是槽位数量， K是映射的数据的总数量：

1. 当 n=1 时， 所有的 k 都要映射到一个槽位上， 函数返回 0， 即 ch(k,1)=0。
2. 当 n=2 时， 为了映射的均匀， 每个槽要映射到 K/2 个 k， 因此需要 K/2 的 k 进行重新映射。
3. 以此类推， 当槽位数量由 n 变化为 n+1 时，需要 K/(n+1) 个 k 进行重新映射。

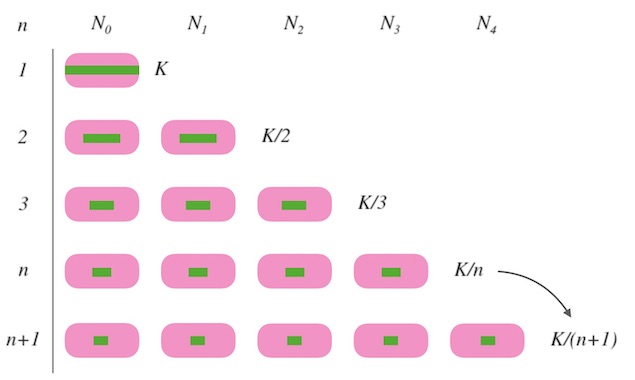
图8.1 - 每次需要 1/(n+1) 份进行重新映射

我们知道了每次需要重新映射多少份，才可以保证映射均匀。 接下来的问题是： 哪些 k 要被重新映射呢？ 就是说在新加槽位的时候，要让哪些 k 跳到新的槽位， 哪些 k 留在老地方不动呢？

Google 的办法是用随机数来决定一个 k 每次要不要跳到新槽位中去。 但是请注意，这里所说的「随机数」是指伪随机数，即只要种子不变，随机序列就不变。 我们程序语言中的随机数发生器都是伪随机的：

>>> random.seed('some-seed')
>>> random.random(), random.random(), random.random()
(0.5294407477447773, 0.9935403183087578, 0.1439482942989072)
>>> random.seed('some-seed')
>>> random.random(), random.random(), random.random()
(0.5294407477447773, 0.9935403183087578, 0.1439482942989072)

对每一个 k , 我们用这个 k 做随机数种子，就得到一个关于 k 的随机序列。 为了保证槽位数量由 j 变为 (j+1) 时有 1/(j+1) 占比的数据会跳到新槽位 (j+1)， 就可以用如下的条件来决定是否重新映射： 如果random.next() < 1 / (j+1) 则跳， 否则留。 那么，我们得到了初步的一个 ch 函数：

int ch(int k, int n) {
  random.seed(k);
  int b = 0;  // This will track ch(k, j+1).
  for (int j = 1; j < n; j++) {
    if (random.next() < 1.0/(j+1)) b = j;
  }
  return b;
}

下面的图8.2是对这个函数的一个演绎。 n 从 1 变化到 5 的过程中， k1 和 k2 每一次都要根据随机序列相应的值和目标分布 1/n 的比较， 来决定留在原来的槽位还是跳到新槽位。

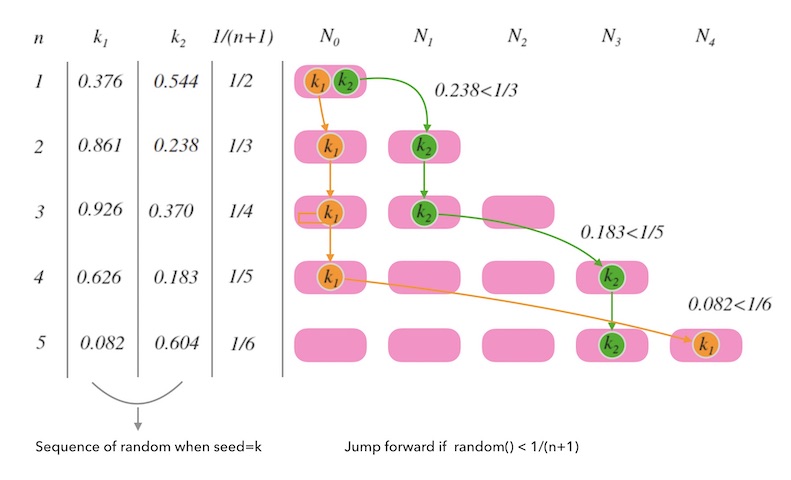
图8.2 - 每次和随机数比较决定是否跳到新槽位

需要注意的是， k 一旦确定， 随机序列就确定了， 每次计算 ch 函数，都会重新初始化随机数种子， 这样后面的 for 循环就是在遍历一个确定的序列而已。 并不是真正的随机数。 就是说， k 一旦确定， 给定一个 n 时， k 的映射结果都是唯一确定的， 也就是一致的。

另一方面，虽然随机序列是由种子决定的， 但是随机序列足够均匀，这才能保证 ch 函数映射结果的均匀性。

ch 函数没有造成全量重新映射， 而是 1/(n+1) 份重新映射， 这个函数已经达到了一致性哈希算法的定义标准。 可以说，跳跃一致性哈希做到了最小化重新映射(minimum disruption)， 做到了完全的一致性。

分析下它的时间复杂度呢？ 显然是 O(n) 。 接下来我们把这个时间复杂度优化到 log 级别。

不难得知， random.next()<1/(j+1) 发生的概率是相对小的。 所以我们的判断条件命中率并不高， 只有少数的 k 选择跳， 这正是优化点， 现在的 j 是一步一步跑的， 那么接下来我们让 j 跳着跑。

上面的 ch 函数中， b 是用来记录 k 最后一次跳入的槽位标号。 假如我们现在处在 k 刚刚跳入最后一个槽位的时刻， 此时一定有 (b+1) 个槽位。 接下来的时刻， 我们要再新增一个槽位变为 b+2 个时， 易知 k 不换槽位的概率是 (b+1)/(b+2)。 假设我们要找的下一个 b 是 j， 就是说，假设当槽位数目到了 j+1 个时 k 跳入最新槽位， 那么， 在此期间， k 保持连续不换槽位的概率是(注意计算的终止项)：

P(stay_until_j)=(b+1)(b+2)∗(b+2)(b+3)∗…∗(j−1)j

化简得， k 连续不跳槽直到增加到 j+1 个槽位才跳的概率为 (b+1)/j。

下面图8.3 中， 虚线框内表示连续不变槽位， 其概率就是各次不变槽位的概率之积。

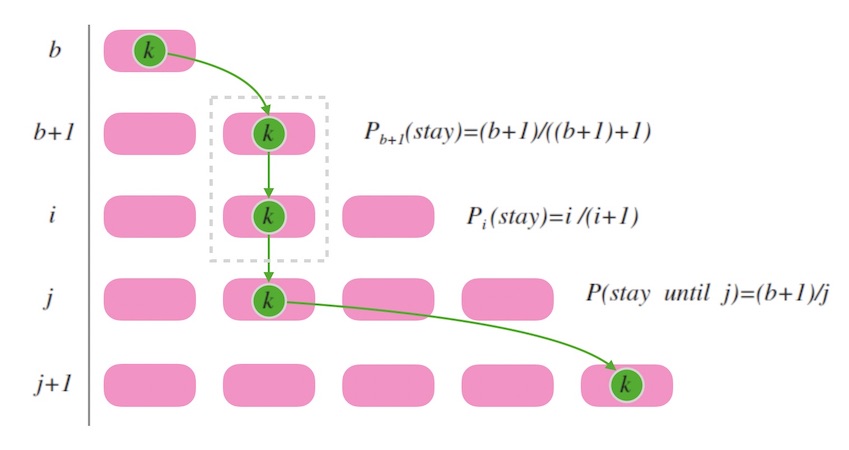
图8.3 - 映射结果连续不变的概率

联系下我们前面设计的 ch 函数， 我们改写函数 ch 如下， 意即， 当符合连续不换槽的概率时， j 直接跳过：

int ch(int k, int n) {
  random.seed(k);
  int b = 0, j = 0;
  while (j < n) {
    if (random.next() < (b+1.0)/j) b = j;
    j += continuous_stays;
  }
  return b;
}

设 r=random.next() 要满足 r<(b+1)/j ， 就必须 j<(b+1)/r ，就是说 j 不得大于 (b+1)/r 才不至于漏掉迭代， 所以 j 最多移动到 (b+1)/r，向下取整即 floor(b+1)/r, 进一步改写 ch 函数如下：

int ch(int k, int n) {
  random.seed(k);
  int b = -1, j = 0;
  while (j < n) {
    b = j;
    r = random.next();
    j = floor((b+1) / r);
  }
  return b;
}

现在来分析下它的时间复杂度。 因为 r 的分布是均匀的， 在槽位数将变化为 i 的时候跳跃发生的概率是 1/i， 那么预期的跳跃次数就是 1/2+..+1/i+..+1/n , 调和级数和自然对数的差是收敛到一个小数的， 所以复杂度是 O(ln(n))。

论文[1]中提到：

It is interesting to note that jump consistent hash makes fewer expected jumps (by a constant factor) than the log2(n) comparisons needed by a binary search among n sorted keys.

意思是， 跳跃一致性哈希算法的复杂度是比二分查找的复杂度 O(log(n)) 要快一些的，因为有一个常数。 我猜了下作者的意思应该是这样的:

O(ln(n))=O(log2nlog2e)

因为 log2e 是一个大于1的数， 所以， O(ln(n)) 虽然在复杂度上和 O(log(n)) 一样，都是对数级别复杂度， 但是，二分查找的复杂度是二分的，底是2， 跳跃一致性哈希的底是 e ， 跳的要更快。

还是没有达到最终 Google 的函数呀？ 因为 Google 的 JumpConsistentHash 函数没有用语言自己的 random , 而是自己做了一个64位的线性同余随机数生成器。

跳跃一致性哈希算法的设计非常精妙， 我认为最美的部分是利用了伪随机数的一致性和分布均匀性。

跳跃一致性哈希的特点

根据论文[1]中的试验数据来看， 跳跃一致性哈希在执行速度、内存消耗、映射均匀性上都比经典的哈希环法要好。

下图是论文[1]中跳跃一致性哈希算法和哈希环法关于运行时间的对比， 可以看到红色的线（jump hash）是明显耗时更低的。

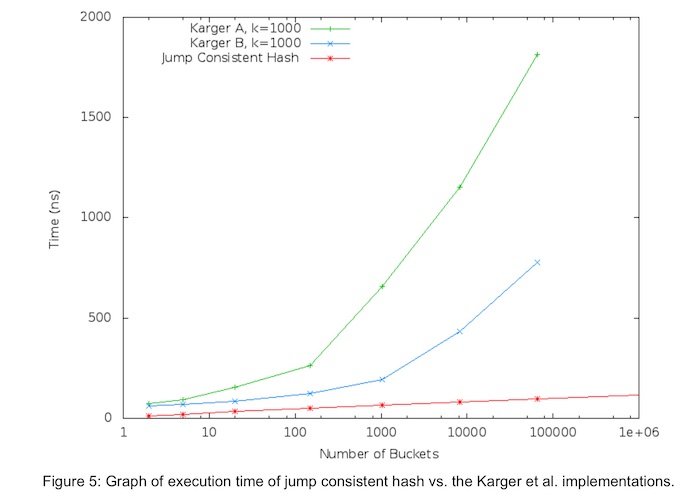
图9.1 - 跳跃一致性哈希和哈希环的执行时间对比

下图是论文[1]中跳跃一致性哈希算法和哈希环法关于映射分布的均匀性的对比， 其中 Standard Error是指分布的标准差， 标准差越小则分布越均匀。 可以看到跳跃一致性哈希的分布要比哈希环的方式均匀的多。 这一点也可以理解， 跳跃一致性哈希的算法设计就是源于对均匀性的推理。

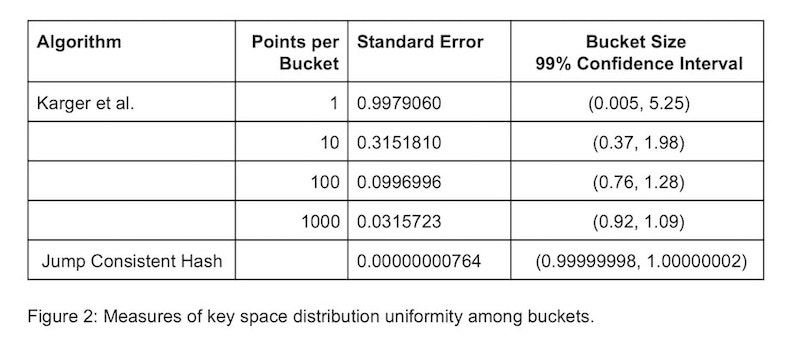图9.2 - 跳跃一致性哈希和哈希环的映射的均匀性对比

关于内存消耗上的对比结果， 其实已然不言自明。 经典的一致性哈希环需要数据结构的支撑， 空间复杂度是 O(N) 的， 而跳跃一致性哈希算法几乎没有额外内存消耗。

一切看上去都很美好, 但是，跳跃一致性哈希算法有两个显著缺点：

• 无法自定义槽位标号

  跳跃一致性哈希算法中， 因为我们没有存储任何数据结构， 所以我们无法自定义槽位标号， 标号是从 00 开始数过来的。

• 只能在尾部增删节点

  下面图9.3， 假如我们在非尾部添加一个新的槽位， 会导致这个位置后续的槽位的标号全部发生变化。 所以在非尾部插入新槽位没有意义， 我们只能在尾部插入。

  

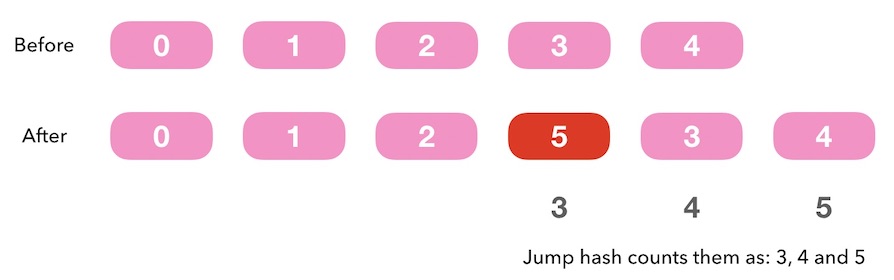
  图9.3 - 跳跃一致性哈希中在非尾部插入新槽位没有意义

  对于在非尾部删除一个槽位也是一样的, 我们只能在尾部删除。

  

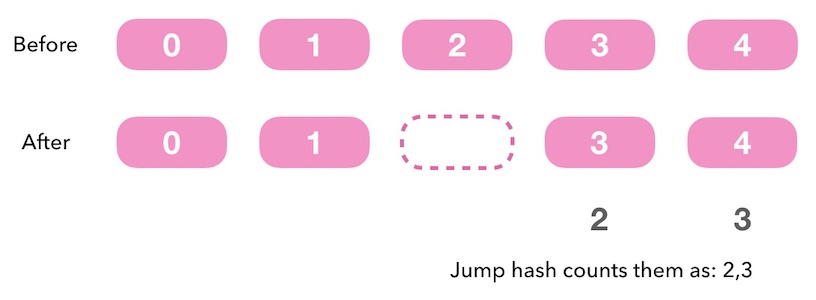
  图9.4 - 跳跃一致性哈希中在非尾部删除槽位

  如果导致后面的槽位全部重新标号，更提不上一致性映射。

跳跃一致性哈希下的热扩容和容灾

回到kvdb的例子上来， 我们讨论下如下问题：

• 扩容： 新加一个节点， 如何做到不停服？
• 容灾： 损失一个节点，如何做到影响最小？

先看第一个问题： 如何做热扩容。

新加一个全新的节点时， 必然要迁移数据才可以服务。 可以采用和一致性哈希环法类似的办法， 即请求中继： 新加入的节点对于读取不到的数据，可以把请求中继(relay)到老节点，并把这个数据迁移过来。

「老节点」是什么？ 假如此次扩容时，节点数目由 n 变为 n+1n+1， 老节点的标号则可以由 ch(k,n) 计算得出， 即节点数量为 n 的时候的 k 的槽位标号。

下图10.1是一个示例， 当新加一个节点 n 时， k 被映射到新的槽位。 老节点标号是 Nold=ch(k,n)。 当一个查询 get(k) 到来， 因为 k 此时映射到的是新节点 n ， 所以可能会查不到数据， 接下来把请求中继到老节点 Nold ， 即可以查到结果。 同时 nn 把 k 对齐到自己这里。

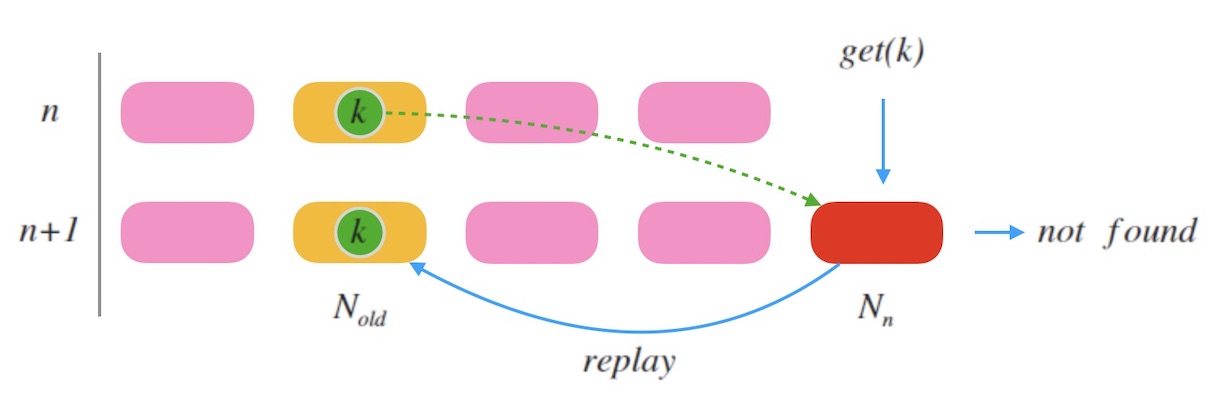
图10.1 - 跳跃一致性哈希中新增节点时做中继

通过这种方式，可以做到整个系统不停服扩容。 关键在于如何找到老节点。

再看第二个问题： 如何做容灾。

先看下，当我们移除一个节点时，会造成什么影响？

假如移除最后一个节点， 如下图10.2中， 尾部节点 N4 被移除后， 整体映射情况和节点数为 n 的时候是一致的。 一切看上去还好。 只要考虑如何备份 N4 上的数据就可以了。 参考上面如何扩容的玩法，可以把尾部节点的数据备份到老节点 (例如，图10.2中 k2 的老节点就是 N3)。

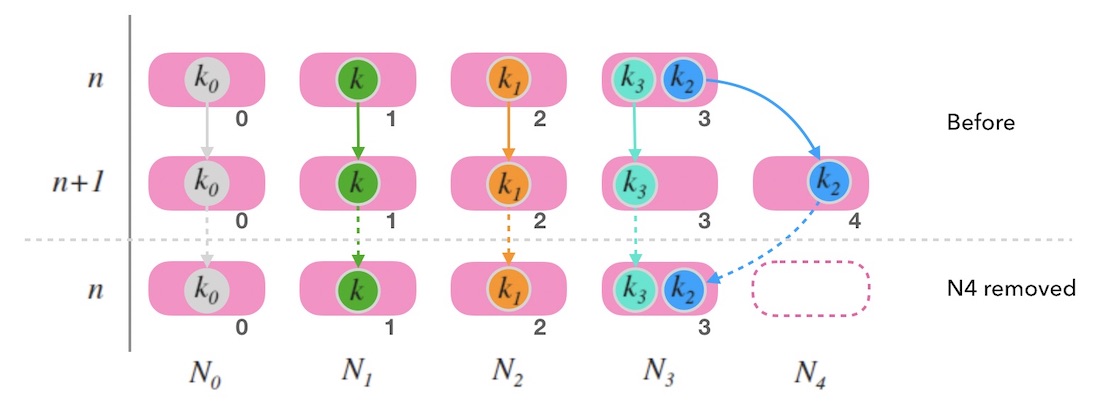
图10.2 - 跳跃一致性哈希中删除尾部节点的情况

但是，移除一个非尾部节点的情况就不一样了。 下面的图10.3中，移除 N1 时，映射的整体结果会发生较大变化， 造成了大面积的映射右偏现象。 原因在于， 虽然跳跃一致性哈希映射到的节点标号和节点数是 n 的情况是一致的， 但是，映射到的节点本身已经变化了。 在这种情况下，因为大量数据的重新映射， 跳跃一致性哈希已经不符合一致性哈希的定义标准， 带来的数据迁移的工作量也是巨大的。

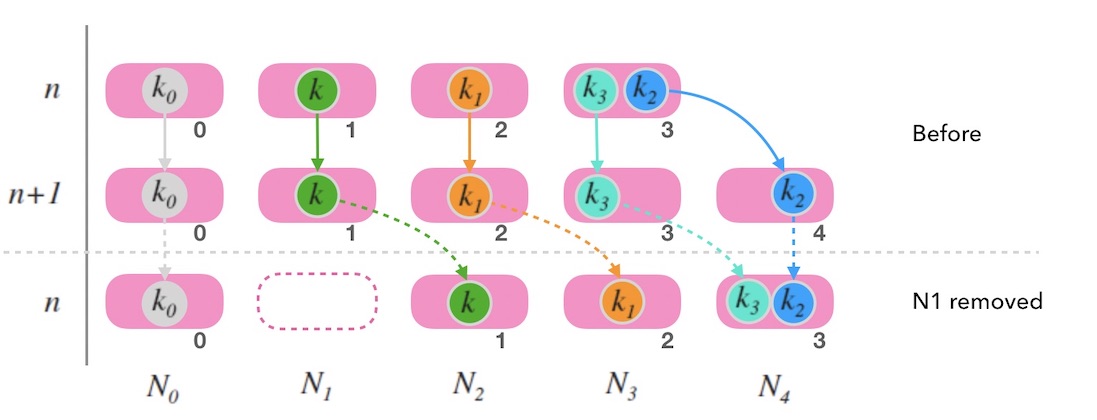图10.3 - 跳跃一致性哈希中删除非尾部节点节点的情况

现实中，节点故障是肯定有可能发生在非尾部节点的。一旦这种情况发生， 除了故障数据丢失的问题之外，还面临大面积的映射偏移的问题。

至此，或许可以想到如何备份来容灾了，在执行数据写操作时，同时写一份数据到备份节点。 备份节点这样选定：

• 尾部节点备份一份数据到老节点。
• 非尾部节点备份一份数据到右侧邻居节点。

我们看下在这个容灾策略下的效果：

• 当删除尾部节点时：

  下图10.4中， 删除了 N4 后， k2 被重新映射到 N3， 因为 N4 的数据在 N3 有备份， 因此正常。

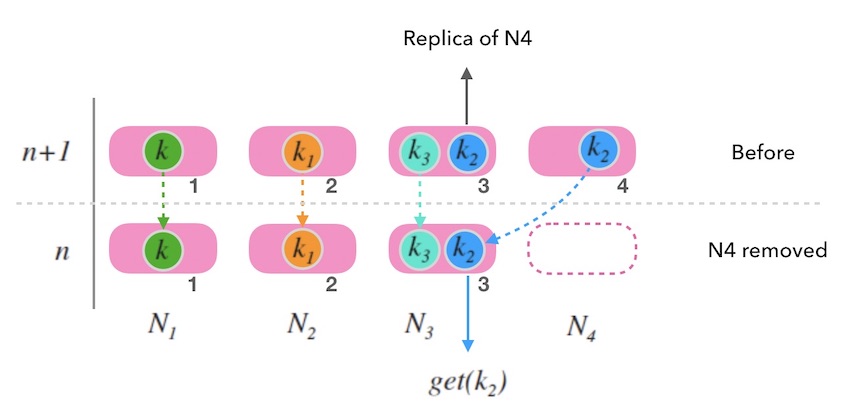  图10.4 - 跳跃一致性哈希中的容灾策略

• 当删除非尾部节点时：

  下图10.5中， 删除了 N1 后， 由于 k， k1， k3 都在邻居节点上有备份， 所以此时映射右偏后并不会造成三个数据丢失， 而且查询也是正确的。

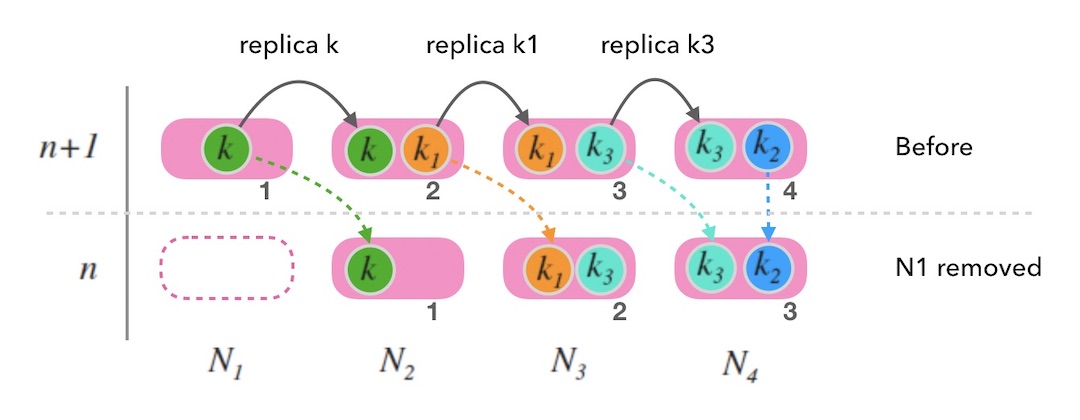  图10.5 - 跳跃一致性哈希中的容灾策略

至此，跳跃一致性哈希下的热扩容和容灾的思路就讨论到这里。 虽然跳跃一致性哈希表现这么简单，思考起来比经典的哈希环法要复杂一些。

带权重的跳跃一致性哈希

最后，讨论下跳跃一致性哈希法如何对映射加权。

我们同样可以尝试虚拟节点(影子节点)的办法来做权重。

下面图11.1中， V(Ni)表示 Ni 的影子节点， 可以看到 N0, N1, N2 的权重比是 3:2:1。 当我们把比重变成 3:3:1 时，和一致性哈希环一样， 可能会引起数据的重新映射，带来数据迁移工作。

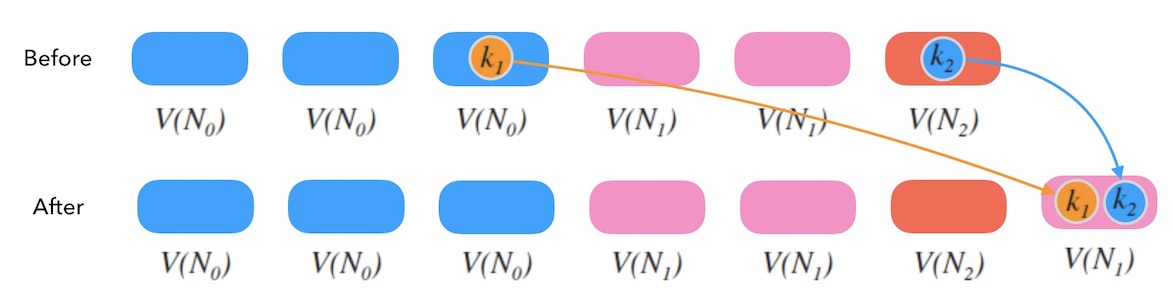
图11.1 - 跳跃一致性哈希的加权

小结

跳跃一致性哈希法最显著的特点是： 实现轻巧、快速、内存占用小、映射均匀、算法精妙。 但是，原始的跳跃一致性哈希算法的缺点也很明显，不支持自定义的槽位标号、而且只能在尾部增删槽位。 不过我们讨论下来，在这个算法下做热扩容和容灾也是有路可循的， 但是理解起来远不及哈希环直观。

一致性哈希算法（四）- Maglev一致性哈希法

Maglev一致性哈希算法

Maglev哈希算法来自 Google ， 在其2016年发布的一篇论文中[1]， 介绍了自2008年起服役的网络负载均衡器Maglev， 文中包括Maglev负载均衡器中所使用的一致性哈希算法，即Maglev一致性哈希 (Maglev Consistent Hashing)。

我们要设计一个一致性哈希算法， 要求映射均匀， 并尽力把槽位变化时的映射变化降到最小（避免全局重新映射）。

Maglev一致性哈希的思路是查表： 建立一个槽位的查找表(lookup table)， 对输入 k 做哈希再取余，即可映射到表中一个槽位。 下面的图1.1是一个示意图， 其中 entry 是查找表，里面记录了一个槽位序列， 查找表的长度为 M， 当输入一个 k 时， 映射到目标槽位的过程就是 entry[hash(k)%M]。

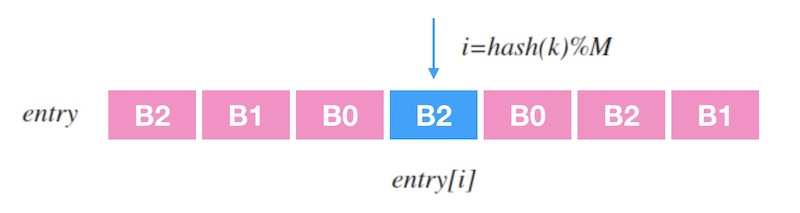
图1.1 - 从查找表中查找槽位

如何查表很好理解。 接下来看，如何生成一张查找表。 先新建一张大小为 M 的待填充的空表 entry。 为每个槽位生成一个大小为 M 的序列 permutation， 叫做「偏好序列」吧。 然后， 按照偏好序列中数字的顺序，每个槽位轮流填充查找表。 将偏好序列中的数字当做查找表中的目标位置，把槽位标号填充到目标位置。 如果填充的目标位置已经被占用，则顺延该序列的下一个填。 这么简短地讲不大容易明白， 看一个例子就可以清楚了。 下面图1.2是论文[1]中的演示填充查找表的原图：

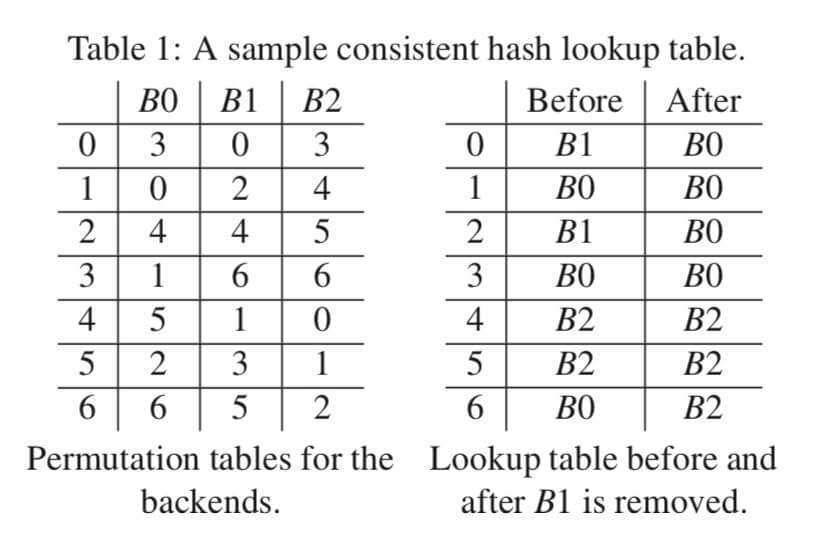
图1.2 - 从偏好序列生成查找表

我做了一张更容易理解的图来理解填表过程。 下面的图1.3中，左边的每一个纵列代表槽位的偏好序列， 右边是我们要填充的查找表。 我们看下整个的填充过程：

1. B0 的偏好序列的第一个数字是 3， 所以填充 B0 到 entry[3]。
2. 轮到 B1 填充了， B1 的偏好序列第一个是 0， 所以填充 B1 到 entry[0]。
3. 轮到 B2 填充了，由于 entry[3]被占用， 所以向下看 B2 偏好序列的下一个数字，是 4， 因此填充 B2 到 entry[4]。
4. 接下来， 又轮到 B0 填充了， 该看它的偏好序列的第2个数字了，是 0，但是 entry[0] 被占用了； 所以要继续看偏好序列的第3个数字，是 4， 同理， 这个也不能用，直到测试到 1 可以用， 则填充 B0 到 entry[1]。
5. 如上面的玩法， 直到把整张查找表填充满。

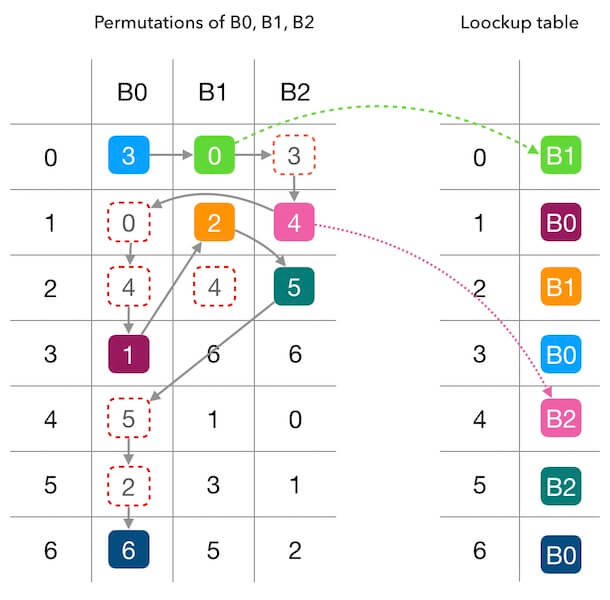
图1.3 - 从偏好序列生成查找表

还有一个问题没有解决：偏好序列是怎么生成的？ 取两个无关的哈希函数 h1 和 h2， 假设一个槽位的名字是 b， 先用这两个哈希函数算出一个 offset 和 skip

offset=h1(b)%Mskip=h2(b)%(M−1)+1

然后， 对每个 j，计算出 permutation 中的所有数字， 即为槽位 b 生成了一个偏好序列：

permutation[j]=(offset+j×skip)%M

可以看到，这是一种类似「二次哈希」的方法， 使用了两个独立无关的哈希函数来减少映射结果的碰撞次数，提高随机性。 生成偏好序列的方法可以有很多种（比如直接采用一个随机序列等）， 不必须是 Google 的这个方法， 在原论文中也提到[1]：

Other methods of generating random permutations, such as the Fisher-Yates Shuffle, generate better quality permutations using more state, and would work fine here as well.

但是无论何种方式，目的都是一样的， 生成的偏好序列要随机、要均匀。

此外，论文中还提到[1]：

M must be a prime number so that all values of skipskip are relatively prime to it.

意思是， 查找表的长度 M 必须是一个质数。 和「哈希表的槽位数量最好是质数」是一个道理， 这样可以减少哈希值的聚集和碰撞，让分布更均匀。

以上就是Maglev一致性哈希的算法的内容， 简单来说：

1. 为每个槽位生成一个偏好序列， 尽量均匀随机。
2. 建表：每个槽位轮流用自己的偏好序列填充查找表。
3. 查表：哈希后取余数的方法做映射。

Maglev哈希算法的边缘情况

不过这个算法还存在一个边缘情况：假如所有的偏好序列都不包含某个数字呢？ 下面的图1.4中，所有偏好序列都不包含 2，导致最终的查找表的 entry[2] 是空的。

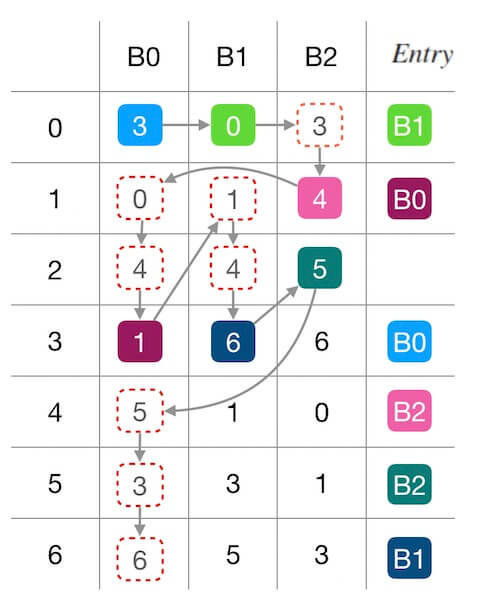
图1.4 - 边缘情况

这种情况出现的概率非常低，但是并不是没有可能。 论文中未对这种情况做出说明，不过还是可以想到解决办法的（当然，方法不止一种）： 如果填充后的查找表有位置没有被填充，可以统计下哪个槽位的占比最小，把那个槽位填到这里。

上面的图1.4中，不巧的是三个槽位都占了2个位置，那么直接随意给标号最小的 B0 好啦。

Maglev哈希的槽位增删分析

我们接下来看下这个算法是否满足一致性哈希算法的定义标准: 映射均匀和一致性。 由于偏好序列中的数字分布是均匀的，查找表是所有偏好序列轮流填充的， 容易知道，查找表也是分布均匀的， 这样，映射也是均匀的。 所以，下面着重分析下槽位增删对映射的干扰， 即分析槽位增删对查找表的填充的影响。

假如，槽位增删导致查找表的某个位置填充的槽位标号发生变化，我们称这是一种「干扰(disruption)」。 槽位增删必然导致填充干扰，我们的目的是追求这个干扰的最小化。

下面的图2.1中演示了删除槽位 B1 前后的填表情况。 红色圆圈内标出了受干扰的填表结果， 可以看到，查找表7个位置中有3个被重新填充。 其中两个位置(第 0，2行)是因为 B1 的移除导致被其他槽位接管， 还有一个第 6 行的 B0→B2 的联动干扰 （因为 B0 接管了 B1 的 entry[2] 导致原本自己的 entry[6] 被 B2 抢占）。

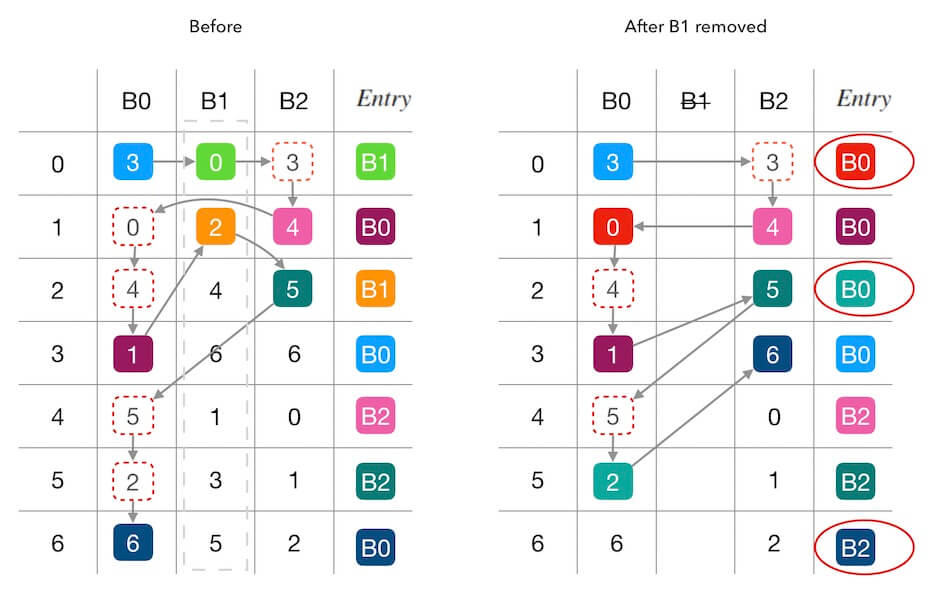
图2.1 - 删除一个槽位B1的情况

下面的图2.2中演示了新增槽位 B3 前后的填表情况。 同样，红色圆圈内标记了受干扰的填表结果， 可以看到，7个位置中有3个被重新填充。 其中两个位置(第 1，5行)是因为 B3 的加入抢占了其他槽位的填充机会， 另一个第 6 行的 B0→B2 则是一种联动干扰。

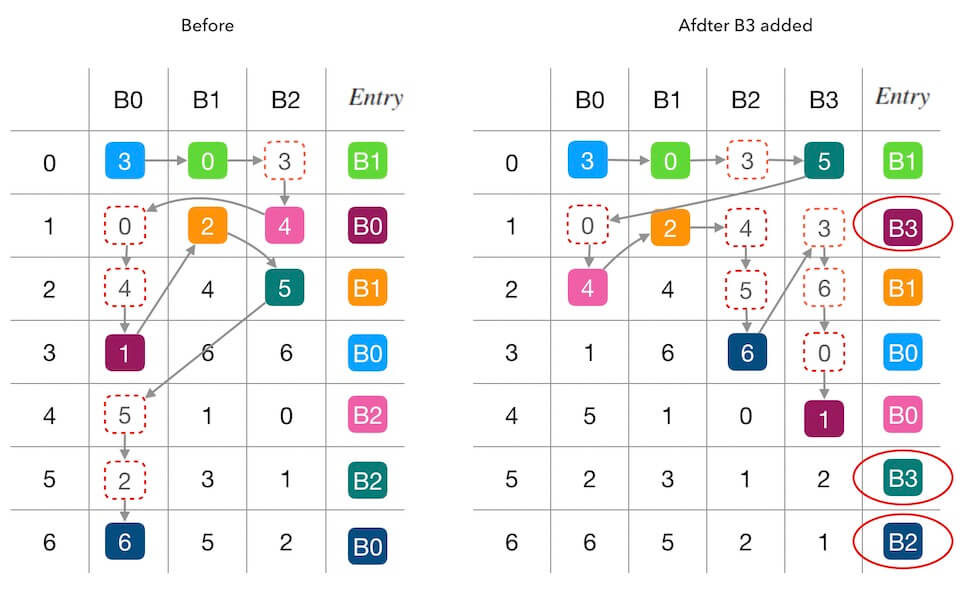
图2.2 - 添加一个新槽位B3的情况

在上面图2.2的基础上，我们继续删除一个槽位 B0， 看下前后的变化。 从下面的图2.3可以看出， 这一次的填表干扰更严重了， 7个里面出现了4个被重新填充。 其中两个（第 3，4 行）是因为 B0 的移除导致位置被其他槽位接管， 还有两个（第 1，6 行， B3→B1 和 B2→B3）都是属于联动干扰。

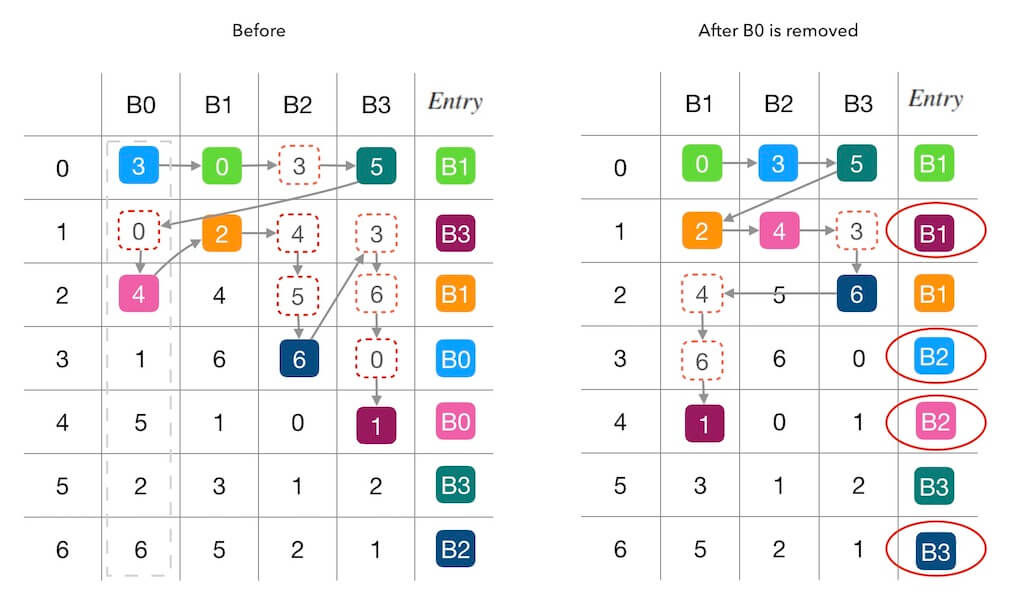
图2.3 - 删除一个新槽位B0的情况

查找表的重填意味着查表时的重新映射。 从上面的三个例子可以看出， Maglev一致性哈希虽然没有导致全量重新映射， 但却没有做到最小化重新映射。 论文[1]中关于Maglev哈希法对槽位增删带来的干扰影响的描述的用词是 minimal disruption， 而不是 minimum disruption 。 论文对于第一个例子的描述是这样的：

After B1 is removed, aside from updating all of the entries that contained B1, only one other entry (row 6) needs to be changed.

意思是，论文指出了联动干扰确实存在， Maglev哈希法并没有实现最小化的干扰。 不过，在 Google 的实际测试中总结出来， 当查找表的长度越大时，Maglev哈希的一致性会越好。

Maglev哈希的复杂度分析

显然，查表的时间复杂度是 O(1) 。

下面分析下建表的复杂度。

论文[1]中给出了填表过程的伪代码实现。 其中，N 是槽位的总数目，permutation[i] 是槽位 i 的偏好序列。 next[i] 用来记录槽位 i 的偏好序列将迭代的下一个位置（即这个序列该跑第几个了）。 对于每一个槽位 i , 我们从它的偏好序列中找出一个候选的、还没占用的位置数字 c , 然后把槽位标号 i 填入查找表 entry 中。

图3.1 - 建表的伪代码

先看下，最坏的时间复杂度是怎样的？ 那肯定是，在查找下一个合适的填充位置的时候， 把所有已经被抢占的位置数字放在这个目标位置的前面， 这样的尝试次数最多！ 这种情况发生在 N=M 且 所有偏好序列完全一样的情况下。 下面的图3.2中描述了这种复杂度最高的情况， 有3个槽位、查找表的长度为3、而且所有偏好序列都一样， 总共需要尝试 4+3+2+1 个数字（也就是 ((4+1)×4)/2， 所以最坏复杂度是 O(((M+1)×M)/2)， 即平方级别的 O(M2)。

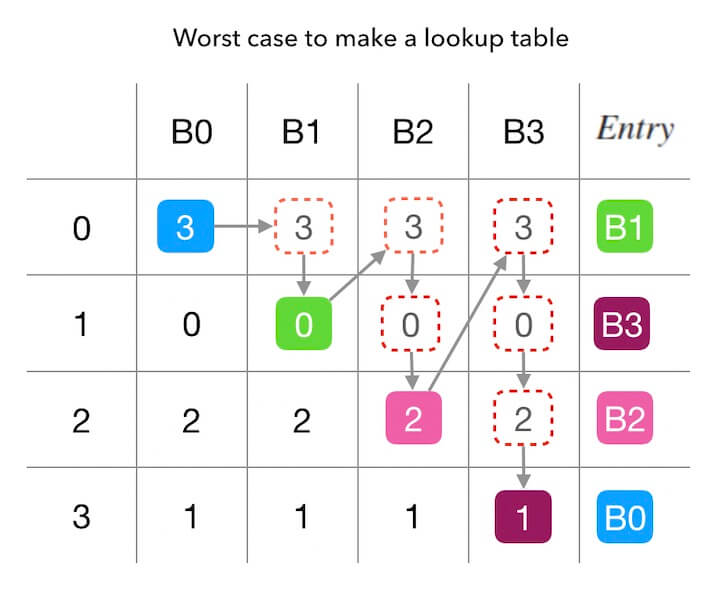
图3.2 - 建表最坏的情况

现在考虑下平均的时间复杂度， 我们就要分析这个过程总共需要尝试多少个数字。 一步一步来想：

• 第一次填表的时候，由于查找表 entry 还是空的，所以第一个数字一定合适， 只需要尝试 1 次。
• 第二次填表的时候，由于前面已经填了一个槽位到 entry 中， 所以空余的空位还有 M−1 个， 所以每个空位被选中的概率是 1/(M−1)。 每次查找一个可以填充位置的过程，都是在一个偏好序列中尝试， 而序列的长度是 M ， 所以需要尝试 M/(M−1)次。
• 依次类推， 当我们已经填充了查找表 entry 的 n 个位置的时候， 我们下一步就需要尝试 M/(M−n)次来找到下一个可以填充的空位置。

计算下来，总共需要尝试的次数是： M/M+M/(M−1)+…+M/(M−(M−1))， 即 ∑Mn=1Mn∑n=1Mn， 是 1 到 1/M 的倒数之和 与 M 的乘积。 调和级数和自然对数的差是收敛到一个小数的， 所以，平均的时间复杂度是对数级别的 O(Mln(M))， 也就是 O(Mlog(M))O(Mlog(M)) (注意到 O(ln(n))=O(log2nlog2e))。

一般选择 M≫NM≫N (M 远大于 n) ， 这样各个槽位的偏好序列更随机、均匀，也不容易发生不同槽位的偏好序列一样的情况。 当然，也不是越大越好， 越大的 M 意味着更高的内存消耗、更慢的建表时长。 结合前面所讲的内容， 应该选择一个远大于 n 的质数当做查找表的大小 M。 论文中提到，在 Google 的实践过程中，一般选择 M 为一个大于 100×N 的质数， 这样各个槽位在查找表上的分布的差异就不会超过 1%。

Maglev哈希的测试表现

论文中对Maglev一致性哈希的测试关注在两个指标： 映射的平均性 和 对槽位变化的适应能力。

下面图4.1对比了 Maglev哈希、 经典的哈希环算法(Karger hash ring) 和 Rendezvous哈希环算法 在不同槽位数量的情况下（对应的查找表大小分别是 6553765537 和 655373655373 ）， 映射结果中占比最大和最小的槽位的占比。 从图中可以看到，两种槽位数量的情况下，Maglev的映射结果中占比最大和占比最小的占比量都非常接近， 也就是说，Maglev一致性哈希的映射平均性非常好。

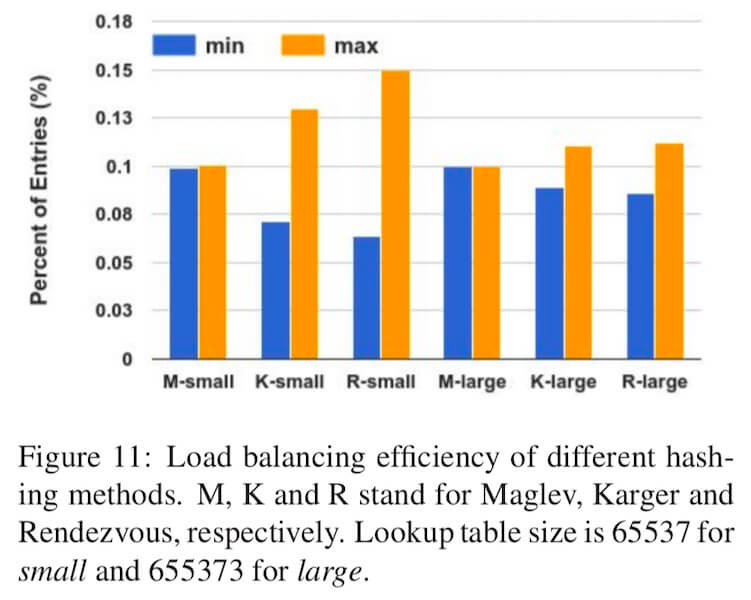
图4.1 - 不同算法的映射结果的最大和最小占比的对比

关于槽位增删对映射一致性的干扰影响，由于哈希环算法实现了最小的重新映射， 所以当删除槽位时（比如节点故障时）哈希环算法可以保证剩余的槽位的映射不受影响。 而我们前面有分析，对于Maglev算法来讲, 则并没有做到最小的重新映射。 下面的图4.2中是 Google 对Maglev负载均衡器做的测试结果， 演示了在相同数量的后端节点、但是不同大小的查找表的情况下(分别是 6553765537 和 655373655373)， 映射结果发生变化的节点的占比相对于节点故障占比的关系。 可以看到，查找表越大，Maglev哈希对槽位增删的容忍能力更强，映射干扰也越小。

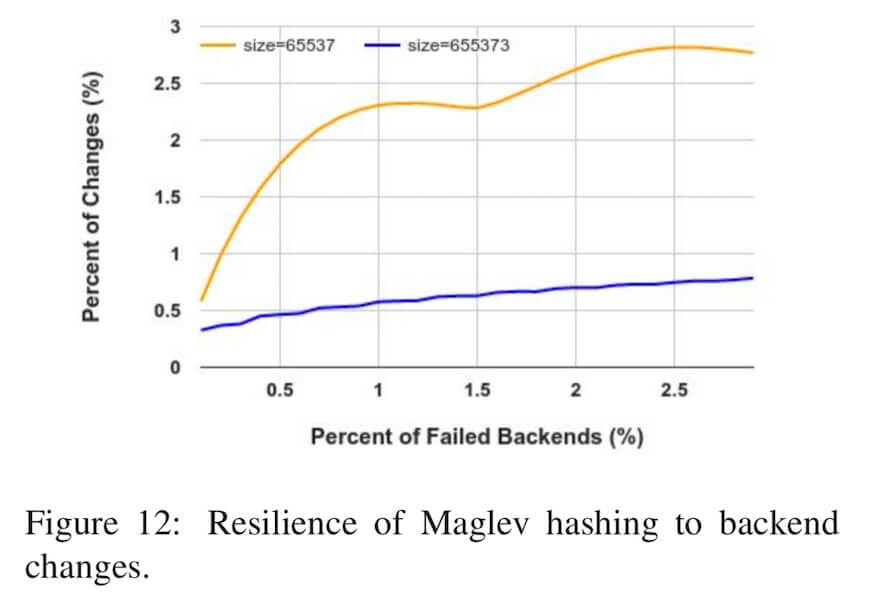图4.2 - 不同节点数量下的映射结果的变化比例和节点故障率之间的关系

不过，即使这样，实际中 Google 仍然选择 6553765537 作为查找表大小。 论文中给出的说法是， 当他们把查找表大小从 6553765537 调大到 655373655373 时， 查找表的生成时间从 1.8ms 升高到了 22.9ms， 所以查找表的大小不是越大越好。 论文中同时提到：

because we expect concurrent backend failures to be rare, and we still have conection tracking as the primary means of protection.

意思是说， 在 Google 的场景下， 并没有把后端槽位的变化带来的干扰看的太重要。 实际上，工程中节点损失是低概率事件， 并且 Google 的设计中主要的保护手段是连接跟踪，而不是完全依赖一致性哈希。 这样，也可以理解了，这个一致性哈希算法的设计上就没有做到最小化干扰的要求。

Maglev哈希的热扩容和容灾

对于Maglev哈希来讲，热扩容或许还可以做，容灾却无法依赖备份的方式进行。

回到kvdb的例子上来， 看一下我们的诉求：

• 扩容： 新加一个节点， 如何做到不停服？
• 容灾： 损失一个节点，如何做到影响最小？

先看第一个问题： 如何做热扩容。

新加一个全新的节点时， 必然要迁移数据才可以服务。 还是采用类似的办法，即请求中继： 新加入的节点对于读取不到的数据，可以把请求中继(relay)到老节点，并把这个数据迁移过来。

老节点是什么呢？ 就是加入新节点之前，数据应该映射到的那个节点。举例子来说， 观察前面的图2.2中，假设数据 k 先前映射到的节点是 B0， 后来因为新加入了节点 B3， 导致 k 现在映射到 B3， 那么 B0 就叫做 k 的老节点。

要知道数据的老节点是什么，就要保存一份加入新节点之前的查找表。 也就是节点要保存两份查找表。如果经最新的查找表映射到的节点上没有数据， 再去经老查找表映射到老节点上去查。

然而第二个问题： 如何做容灾， 则没那么容易。

回顾下前面章节中的图2.2和图2.3。

图2.3演示了删除一个节点的情况，为了演示方便，这里直接把图2.3照搬下来：

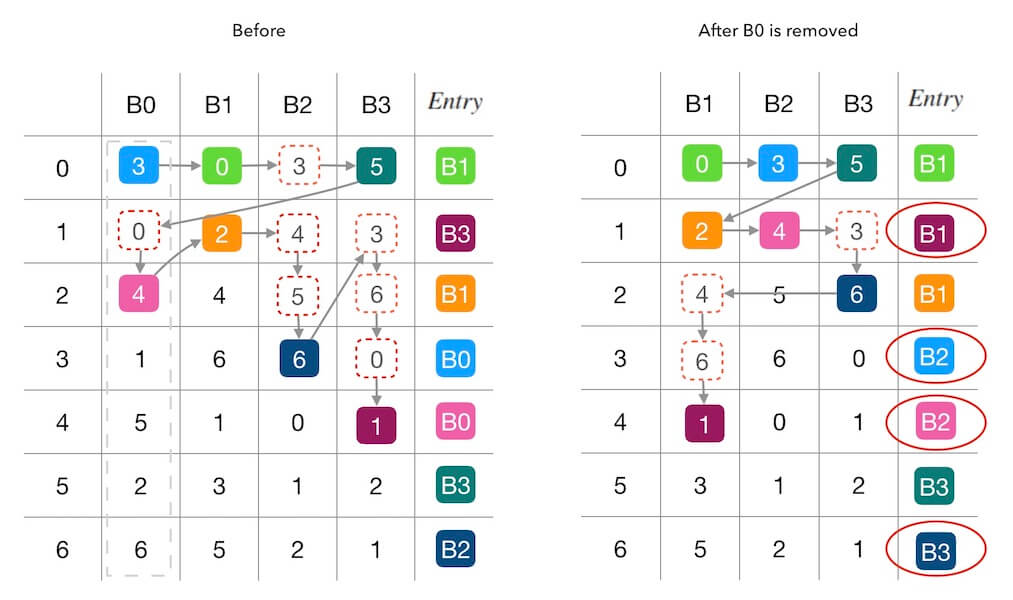
图2.3 - 删除一个新槽位B0的情况

图2.2中演示了新增节点前后的填表情况，如果我们从右往左看，它也可以演示删除节点的情况， 就是下面图5.1的样子：

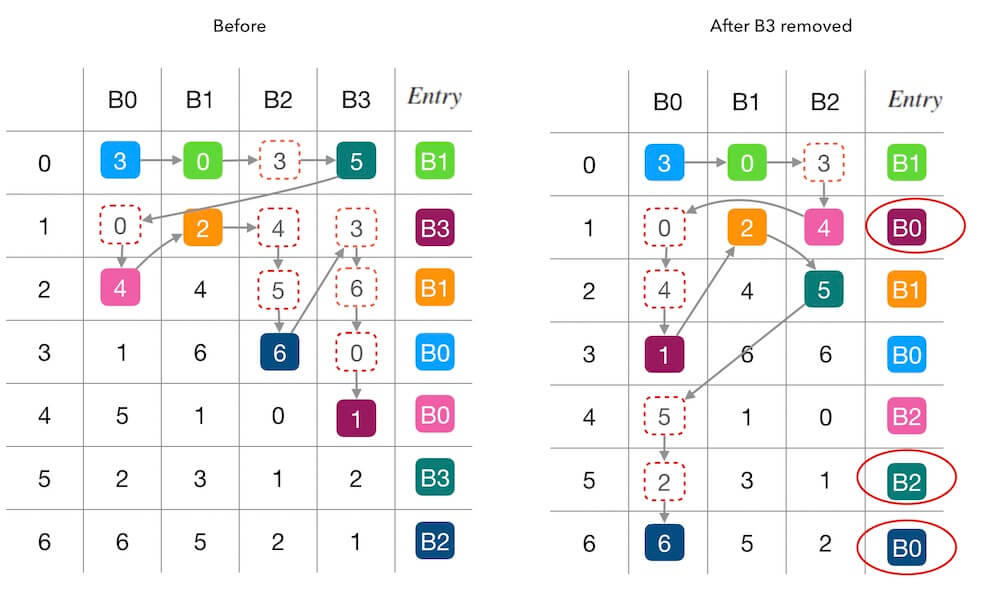
图5.1 - 删除一个槽位B3的情况

可以观察到两个图中都是从完全一样的状况、完全一样的表格，分别删除不同节点的情况。 图2.3中，删除 B0 后，导致了一个 B3→B1 的映射变化。 所以， 我们需要把 B3 的数据备份到 B1 上，才可以应对这一变化，而不丢数据、不停服。 图5.1中，删除 B3 后则导致了 B3→B0 和 B3→B2的映射变化， 意思是， 在损失节点 B3 之后， B3 中的数据一部分会映射到 B0 上， 一部分又会映射到 B2 上， 我们除非把 B3 的数据全部备份一份到 B0, B1, B2 上， 否则没有很好的办法做 B3 的数据备份。

这样，关于容灾这个话题， 我的结论是没有很好的办法做数据备份，所以无法做不停服的容灾处理。 (需要注意：这部分并不是论文中的内容，而是我个人的分析结论。)

论文中所讨论的Maglev哈希算法的应用场景是负载均衡，确切的说是弱状态化的后端的负载均衡。 如果后端节点的数据是类似数据库性质的强状态化数据，那么就会有容灾设计的问题。 如果后端节点是无状态的、或者是弱状态的（如缓存）， Maglev哈希算法的一致性的特点还是有好处的：比如降低故障情况下的缓存击穿的比例、连接重新建立的比例等等。

带权重的Maglev哈希

Maglev哈希做到了尽量平均的映射分布，但是，如果槽位之间不是平权的呢？ 关于带权重的Maglev哈希，论文中只提了一句话：

Heterogeneous backend weights can be achieved by altering the relative frequency of the backends’ turns.

意思是，可以通过改变槽位间填表的相对频率来做加权。 就是不「轮流」填了，可以你填1次，我填3次。 填表越频繁的槽位，权重就越大。

最后我们再玩一次填表游戏。下面的图6.1中，假设 B0 的权重是 2， 其他的槽位的权重都是 1， 也就是其他槽位每填表一次， B0 填表两次。 可以观察到，填表的结果上， B0 的席位占比 4/7， 符合权重的设定。

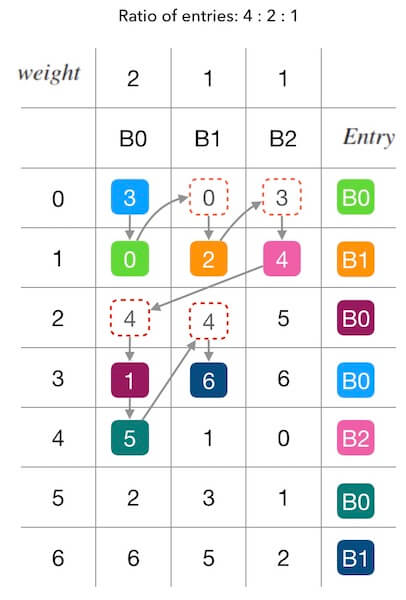
带权重的填表过程

小结

Maglev哈希是 Google 在自家的负载均衡器Maglev中使用的一致性哈希算法。 槽位变化时，虽然避免了全局重新映射，但是没有做到最小化的重新映射。 映射的均匀性非常好。映射的时间复杂度是 O(1)， 建立查找表的时间复杂度是 O(Mlog(M))。 可以通过改变填表的相对频率来实现加权。 难以实现后端节点的数据备份逻辑，因此工程上更适合弱状态后端的场景。

三个方法的总结

最后对一致性哈希环、跳跃一致性哈希和Maglev哈希做一次总结：

	均匀性	最小化重新映射	时间复杂度	加权映射	热扩容 & 容灾
哈希环	⍻	✔	O(log(n))	✔	✔
跳跃一致性哈希	✔	✔	O(log(n))	✔	✔
Maglev哈希	✔	✘	O(1)O(1)	✔	✘