使用递归的思路

  1. 找出简单的基线条件
  2. 每次递归都必须缩小问题的规模，使其符合基线条件
  3. 假设递归可用

示例

一个人赶着鸭子去每个村卖,每经过一个村庄卖出去所赶鸭子的一半又一只,这样他经过7个村子后还剩两只鸭子，问他出发时共赶多少只鸭?

1
2
3
4
5
6
7
8
9
10
def func(num,count):
	if count == 7:
		return num
	else:
		count += 1
		new_num = 2 * (num + 1) 
		return func(new_num,count)

count = 0
print(func(2,count))

经验:
对计数问题,不一定要使用for each in range(7),也可以把count作为函数参数传入.

  1. 添加一个alist参数,有三种方法:

    1. 使用闭包
    2. 使用global
    3. 直接当作函数参数使用

    角谷理论:输入自然数,若为偶数则将其除以2,若为奇数,将其乘以3后加1,经过有限次运算后,总可以得到1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    def func(num):
        def wrap(num,alist):
            if num == 1:
                alist.append(1)
                return alist
            else:
                alist.append(num)
                if num % 2 == 0:
                    num //= 2
                    return wrap(num,alist)
                else:
                    num = 3*num + 1
                    return wrap(num,alist)

        alist = []
        return wrap(num,alist)

    print(func(22))
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    def func(num):
        global alist
        if num == 1:
            alist.append(1)
            return alist
        else:
            alist.append(num)
            if num % 2 == 0:
                num //= 2
                return func(num)
            else:
                num = 3*num + 1
                return func(num)

    alist = []
    print(func(22))
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    def func(num,alist):
    	if num == 1:
    		alist.append(1)
    		return alist
    	else:
    		alist.append(num)
    		if num % 2 == 0:
    			num //= 2
    			return func(num,alist)
    		else:
    			num = 3*num + 1
    			return func(num,alist)

    print(func(22,[]))

尾递归

尾递归就是把当前的运算结果（或路径）放在参数里传给下层函数

非尾递归，下一个函数结束以后此函数还有后续，所以必须保存本身的环境以供处理返回值。

1
2
3
4
5
6
function story() {    从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story() // 尾递归，进入下一个函数不再需要上一个函数的环境了，得出结果以后直接返回。
}

function story() {    从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story()，小和尚听了，找了块豆腐撞死了 // 非尾递归，下一个函数结束以后此函数还有后续，所以必须保存本身的环境以供处理返回值。
}

尾递归和一般的递归不同在对内存的占用，普通递归创建stack累积而后计算收缩，尾递归只会占用恒量的内存（和迭代一样）。SICP中描述了一个内存占用曲线，用以上答案中的Python代码为例（普通递归）：

1
2
3
4
5
def recsum(x):
  if x == 1:
    return x
  else:
    return x + recsum(x - 1)

当调用recsum(5)，Python调试器中发生如下状况：

1
2
3
4
5
6
7
8
9
10
recsum(5)
5 + recsum(4)
5 + (4 + recsum(3))
5 + (4 + (3 + recsum(2)))
5 + (4 + (3 + (2 + recsum(1))))
5 + (4 + (3 + (2 + 1)))
5 + (4 + (3 + 3))
5 + (4 + 6)
5 + 10
15

这个曲线就代表内存占用大小的峰值，从左到右，达到顶峰，再从右到左收缩。而我们通常不希望这样的事情发生，所以使用迭代，只占据常量stack space(更新这个栈！而非扩展他)。
-——————–
（一个替代方案：迭代）

1
2
for i in range(6):
  sum += i

因为Python，Java，Pascal等等无法在语言中实现尾递归优化(Tail Call Optimization, TCO)，所以采用了for, while, goto等特殊结构代替recursive的表述。Scheme则不需要这样曲折地表达，一旦写成尾递归形式，就可以进行尾递归优化。
-——————–
Python中可以写（尾递归）：

1
2
3
4
5
def tailrecsum(x, running_total=0):
  if x == 0:
    return running_total
  else:
    return tailrecsum(x - 1, running_total + x)

理论上类似上面：

1
2
3
4
5
6
7
tailrecsum(5, 0)
tailrecsum(4, 5)
tailrecsum(3, 9)
tailrecsum(2, 12)
tailrecsum(1, 14)
tailrecsum(0, 15)
15

观察到，tailrecsum(x, y)中形式变量y的实际变量值是不断更新的，对比普通递归就很清楚，后者每个recsum()调用中y值不变，仅在层级上加深。所以，尾递归是把变化的参数传递给递归函数的变量了。
怎么写尾递归？形式上只要最后一个return语句是单纯函数就可以。如：

1
return tailrec(x+1);

而

1
return tailrec(x+1) + x;

则不可以。因为无法更新tailrec()函数内的实际变量，只是新建一个栈。

但Python不能尾递归优化（Java不行，C可以，我不知道为什么），这里是用它做个例子。

如何优化尾递归：
在编译器处理过程中生成中间代码（通常是三地址代码），用编译器优化。

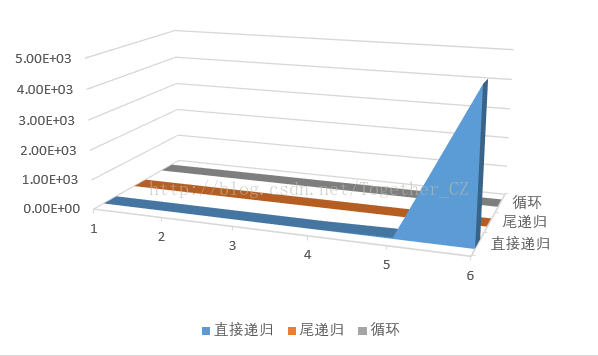
python使用递归、尾递归、循环三种方式实现斐波那契数列

  • 尾递归就是从最后开始计算, 每递归一次就算出相应的结果, 也就是说, 函数调用出现在调用者函数的尾部, 因为是尾部, 所以根本没有必要去保存任何局部变量. 直接让被调用的函数返回时越过调用者, 返回到调用者的调用者去。
  • 尾递归就是把当前的运算结果（或路径）放在参数里传给下层函数，深层函数所面对的不是越来越简单的问题，而是越来越复杂的问题，因为参数里带有前面若干步的运算路径。
  • 尾递归是极其重要的，不用尾递归，函数的堆栈耗用难以估量，需要保存很多中间函数的堆栈。直接递归的程序中需要保存之前n步操作的所有状态极其耗费资源，而尾递归不需要，尾部递归是一种编程技巧。
  • 尾部递归的函数有助将算法转化成函数编程语言，而且从编译器角度来说，亦容易优化成为普通循环。这是因为从电脑的基本面来说，所有的循环都是利用重复移跳到代码的开头来实现的。如果有尾部归递，就只需要叠套一个堆栈，因为电脑只需要将函数的参数改变再重新调用一次
  • 为了加深对尾递归、递归和循环的对比，这里以斐波那契数列的实现举例：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import time
 
def Fib_recursion(num):
    '''
    直接使用递归法求解斐波那契数量的第num个数字
    '''
    if num<2:
        return num 
    return Fib_recursion(num-1)+Fib_recursion(num-2)
 
 
def Fib_tail_recursion(num,res,temp):
    '''
    使用尾递归法求解斐波那契数量的第num个数字
    '''
    if num==0:
        return res 
    else:
        return Fib_tail_recursion(num-1, temp, res+temp)
 
 
def Fib_circle(num):
    '''
    直接使用循环来求解
    '''
    a=0
    b=1
    for i in range(1,num):
        c=a+b
        a=b
        b=c 
    return c 
 
 
if __name__ == '__main__':
    num_list=[5,10,20,30,40,50]
    for num in num_list:
        start_time=time.time()
        print Fib_recursion(num)
        end_time=time.time()
        print Fib_tail_recursion(num,0,1)
        end_time2=time.time()
        print Fib_circle(num)
        end_time3=time.time()
        print '正在求解的斐波那契数字下标为%s' %num
        print '直接递归耗时为 ：', end_time-start_time
        print '尾递归调用耗时为：', end_time2-end_time
        print '直接使用循环耗时为：', end_time3-end_time2

画图图表更加清晰地可以看到差距：

img