第1-3章
数据分析分为以下几个大类:
- 与外部世界交互
阅读编写多种⽂件格式和数据商店; - 数据准备
清洗、修改、结合、标准化、重塑、切⽚、切割、转换数 据,以进⾏分析; - 转换数据
对旧的数据集进⾏数学和统计操作,⽣成新的数据集(例如,通过各组变量聚类成⼤的表); - 建模和计算
将数据绑定统计模型、机器学习算法、或其他计算⼯具; - 展示
创建交互式和静态的图表可视化和⽂本总结
模块命名惯例
1 | import numpy as np |
⾏话:
- 数据规整(Munge/Munging/Wrangling)
指的是将⾮结构化和(或)散乱数据处理为结构化或整洁形式的整个过程。
Munge这个词跟Lunge押韵。 - 伪码(Pseudocode)
算法或过程的“代码式”描述,⽽这些代码本身并不是实际有效的源代码。
使用ipython
运行py文件:
%run hello_world.py补全方法:
因为ipython本身就是增强交互版的shell,比起原生的shell,还可以使用tab自动补全方法: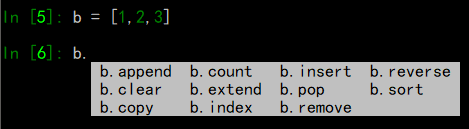
这同样适用于模块和函数的参数: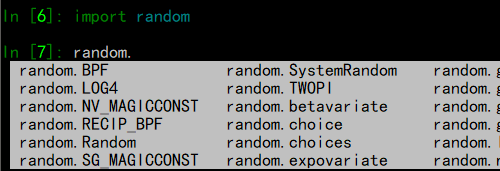
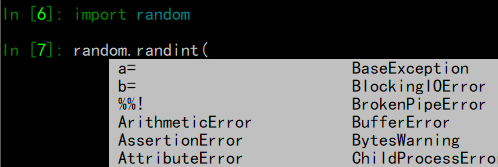
注意:默认情况下,tab补全会自动隐藏魔术⽅法和内部的“私有”⽅法和属性
使用
?显示对象的信息:
(前/后都可以:eg:?b,b?)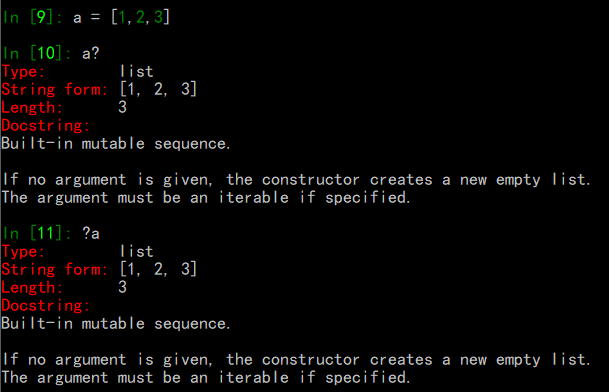
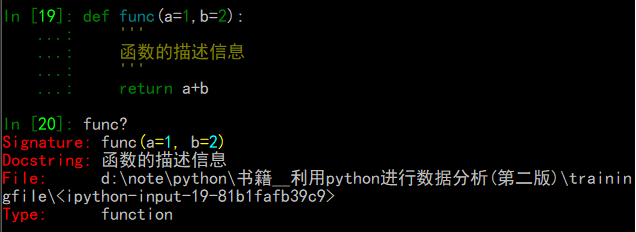
使用
??显示函数源码: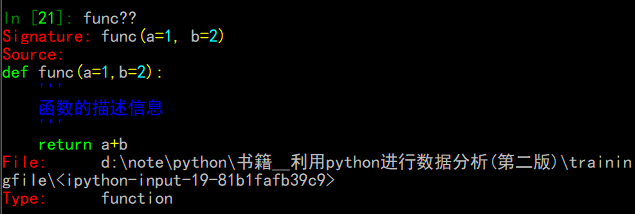
%paste:直接运行剪贴板的代码: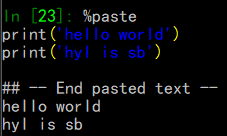
%cpaste:粘贴任意多的代码再运⾏。魔术命令:
IPython中特殊的命令(Python中没有)被称作“魔术”命令。这些命令可以使普通任务更便捷,更容易控制IPython系统。
python知识复习:
Python解释器同⼀时间只能运⾏⼀个程序的⼀条语句。
强类型化语⾔:
意味着每个对象都有明确的类型(或类),不会发默许转换:1
2
3
4a = 4
# js会默许a变成字符串类型,然后拼接成54
# py中,a的类型已经确定,不会默许转化类型
print('5' + a)判断强类型语言的标准:
如果语言经常隐式地转换变量的类型,那这个语言就是弱类型语言,如果很少会这样做,那就是强类型语言。1
2
3
4a = 1
# py也有默许转换,但是只会发⽣在特定的情况下
# 此时a会从int改为float
print(1.0 + a)静态语言和动态语言的区别:
在编译时检查类型的语言是静态类型语言,在运行时检查类型的语言是动态类型语言。
静态类型需要声明类型(有些现代语言使用类型推导避免部分类型声明)Fortran和Lisp是最早的两门语言,现在仍在使用,它们分别是静态类型语言和动态类型语言。所以python是动态强类型语言.
标量:
标量类型,即标准库中内建的类型(None,str,bytes,float,bool,int)datatime:
datetime.datetime是不可变类型1
2
3
4
5
6
7
8
9
10
11
12
13
14from datetime import datetime, date, time
dt = datetime(2011,10,29,20,30,21)
print(dt.day) # 29
print(dt.minute) # 30
print(dt.date()) # 2011-10-29
print(dt.time()) # 20:30:21
print(dt.strftime('%m/%d/%Y %H:%M')) # 10/29/2011 20:30
# 转为datetime对象 2009-10-31 00:00:00
print(datetime.strptime('20091031','%Y%m%d'))
# 替换time字段
dt.replace(minute=0,second=0)两个datetime对象的差会产⽣⼀个datetime.timedelta类型:
1
2
3
4
5
6
7
8
9
10
11from datetime import datetime, date, time
dt1 = datetime(2011,10,29,20,30,21)
dt2 = datetime(2011,11,15,22,30)
delta = dt2 - dt1
print(delta) # 17 days, 1:59:39
print(type(delta)) # <class 'datetime.timedelta'>
# 将timedelta添加到datetime,会产⽣⼀个新的偏移datetime:
print(dt1 + delta) # 2011-11-15 22:30:00加号运算符将元组串联起来:
1
2
3
4
5
6
7
8
9x = (1,2,3)
y = (4,5,6)
print(id(x)) # 2575049627832
print(id(y)) # 2575049655352
z = x + y
print(z) # (1, 2, 3, 4, 5, 6)
print(id(z)) # 2575048177896乘法只是引用对象,并没有复制对象
1
2
3
4
5
6
7
8
9
10x = [[1]]
y = x * 4
print(y)
# [[1], [1], [1], [1]]
# 乘法只是引用对象,并没有复制对象
print(id(y[0])) # 1782212092424
print(id(y[1])) # 1782212092424
print(id(y[2])) # 17822120924241
2
3
4
5
6
7
8
9
10x = (1,)
y = x * 4
print(y)
# (1, 1, 1, 1)
# 乘法只是引用对象,并没有复制对象
print(id(y[0])) # 140720600772352
print(id(y[1])) # 140720600772352
print(id(y[2])) # 140720600772352一般将将不需要的变量使⽤下划线:
1
2values = (1,2,3,4)
a,b,*_ = valueslist也支持拆包:
1
2
3values = [1,2,3,4]
a,b,c,*_ = values
print(a,b,c) # 1 2 3list就是数组.
所以lsit.append比list.insert复杂度低的主要原因不是index的查找,而是因为对后续
元素的引⽤必须在内部迁移,以便为新元素提供空间。不要使用+来拓展list,应该使用extend
通过加法将列表串联的计算量较⼤,因为要新建⼀个列表,并且要复制对象。内建的二分查找:bisect模块:
- bisect.bisect可以找到插⼊值的位置,
- bisect.insort是向这个位置插⼊值
1
2
3
4
5
6
7
8import bisect
c = [1,3,5,7,9]
print(bisect.bisect(c,4)) # 2
print(c) # [1, 3, 5, 7, 9]
bisect.insort(c,6)
print(c) # [1, 3, 5, 6, 7, 9]bisect模块不会检查列表是否已排好序因此,对未排序的列表使⽤bisect不会产⽣错误,但结果不⼀定正确。
一旦要同时迭代多个序列就要想到使用zip:
1
2
3
4
5
6
7
8
9seq1 = ['foo','bar','baz']
seq2 = ['one','two','three']
for i,(a,b) in enumerate(zip(seq1,seq2)):
print('{0}: {1},{2}'.format(i,a,b))
# 0:foo,one
# 1:bar,two
# 2:baz,three1
2
3
4
5
6
7
8
9
10
11x = [1,2,3,4]
y = [1,2,3,4]
z = [1,2,3,4]
for each in iter(zip(x,y,z)):
print(each)
# (1, 1, 1)
# (2, 2, 2)
# (3, 3, 3)
# (4, 4, 4)zip还可以用来解压缩:
1
2
3
4
5
6
7
8
9x = [1,2,3,4]
y = [1,2,3,4]
z = [1,2,3,4]
a,b,c,d = zip(*(x,y,z))
print(a) # (1, 1, 1)
print(b) # (2, 2, 2)
print(c) # (3, 3, 3)
print(d) # (4, 4, 4)使用zip将两个序列配对组合成字典:
1
2
3
4
5seq1 = ['foo','bar','baz']
seq2 = ['one','two','three']
x = dict(zip(seq1,seq2))
print(x) # {'foo': 'one', 'bar': 'two', 'baz': 'three'}删除字典不仅可以使用pop,还可以使用del
1
2
3
4x = {'hyl':89,'dsz':100,'czj':50}
del x['hyl']
print(x) # {'dsz': 100, 'czj': 50}虽然字典的键值对没有顺序,这两个⽅法可以⽤相同的顺序输出键和值:
1
2
3
4x = {'hyl':1,'dsz':2,'czj':3,'jzr':4}
print(list(x.keys())) # ['hyl', 'dsz', 'czj', 'jzr']
print(list(x.values())) # [1, 2, 3, 4]Python 字典 setdefault() 函数:获取,获取不到就设置为键.
和get()方法类似, 如果键不存在于字典中,将会添加键并将值设为默认值。1
2
3
4
5
6
7
8
9x = {'hyl':1,'dsz':2,'czj':3,'jzr':4}
a = x.setdefault('hyl',9)
print(a,x)
# 1 {'hyl': 1, 'dsz': 2, 'czj': 3, 'jzr': 4}
b = x.setdefault('yyy',9)
print(b,x)
# 9 {'hyl': 1, 'dsz': 2, 'czj': 3, 'jzr': 4, 'yyy': 9}将单词按字母分类:
1
2
3
4
5
6
7
8x = ['apple','box','class','an']
d = {}
for each in x:
letter = each[0]
d.setdefault(letter,[]).append(each)
print(d)
# {'a': ['apple', 'an'], 'b': ['box'], 'c': ['class']}集合的所有逻辑运算都有原地方法和非原地方法:
1
2
3
4
5
6
7
8
9s1 = set([1,2,3])
s2 = set([2,3,4])
# 非原地实现方法
x = s1 | s2
print(x) # {1, 2, 3, 4}
# 原地实现方法
s1 |= s2
print(s1) # {1, 2, 3, 4}set某种意义和tuple是完全相反的:
tuple本身是不可变对象,但是tuple内部对象可以是可变的.虽然set本身是可变对象,但是内部元素必须是不可变对象:
(因为内部元素必须进行哈希映射)
1
2
3
4
5s1 = set([1,2,3,4])
print(id(s1)) # 1642137660552
s1.add(5)
print(id(s1)) # 16421376605521
2# TypeError: unhashable type: 'list'
s1 = set([1,2,3,4,[7,8,9]])柯⾥化(currying):
其实就是使用偏函数冻结一部分参数1
2
3
4
5
6from functools import partial
def func(x,y):
return x + y
func2 = partial(func,5)itertools模块:
groupby分组。参数为序列和函数。函数返回相同值的序列为一组1
2
3
4
5
6
7
8
9
10
11
12import itertools
first_letter = lambda x: x[0]
names = ['Alan', 'Adam', 'Wes', 'Will', 'Albert', 'Steven']
for letter, names in itertools.groupby(names, first_letter):
print(letter, list(names)) # names is a generator
# A ['Alan', 'Adam']
# W ['Wes', 'Will']
# A ['Albert']
# S ['Steven']
第4章 NumPy基础:数组和⽮量计算
NumPy的部分功能如下:
- ndarray,⼀个具有⽮量算术运算和复杂⼴播能⼒的快速且节省空间的多维数组。
- ⽤于对整组数据进⾏快速运算的标准数学函数(⽆需编写循环)。
- ⽤于读写磁盘数据的⼯具以及⽤于操作内存映射⽂件的⼯具。
- 线性代数、随机数⽣成以及傅⾥叶变换功能。
- ⽤于集成由C、C++、Fortran等语⾔编写的代码的A C API。
NumPy可以⾼效处理⼤数组的数据。这是因为:
- NumPy是在⼀个连续的内存块中存储数据,独⽴于其他Python内置对象。NumPy的C语⾔编写的算法库可以操作内存,⽽不必进⾏类型检查或其它前期⼯作。⽐起Python的内置序列,NumPy数组使⽤的内存更少。
- NumPy可以在整个数组上执⾏复杂的计算,⽽不需要Python的for循环。
4.1 NumPy的ndarray:⼀种多维数组对象
NumPy最重要的⼀个特点就是其N维数组对象(即ndarray).既然是一个数组对象,所以他也是一个容器,其语法跟标量元素之间的运算⼀样。
1 | import numpy as np |
ndarray对象是⼀个通⽤的同构数据多维容器。
每个数组都有⼀个shape和⼀个dtype:
- shape
表示各维度⼤⼩的元组 - dtype
⽤于说明数组数据类型的对象
1 | import numpy as np |
创建ndarray
1 | import numpy as np |
因为data2是列表的列表,NumPy数组arr2的两个维度的shape
是从data2引⼊的。可以⽤属性ndim和shape验证:
1 | import numpy as np |
所以就是说,ndarray.shape表示了这个多维数组的形状:
1 | (2,3)表示2行3列 |
1 | import numpy as np |
另外创建数组的函数:
zeros/ones:
创建指定⻓度或形状的全0或全1数组。empty:
创建⼀个没有任何具体值的数组
arange:
Python内置函数range的数组版:
1 | import numpy as np |
np.empty返回的是⼀些未初始化的垃圾值。
1 | import numpy as np |
创建数组函数:
| 函数 | 说明 |
|---|---|
| array | 将输入数据(列表、元组、数组或其它序列类型)转换为 ndarray.要么推断出 dtype,要么特别指定dtype.默认直接复制输入数据 |
| asarray | 将输入转换为 ndarray,如果输入本身就是一个 narray就不进行复制 |
| arange | 类似于内置的range,但返回的是一个narray而不是列表 |
| ones,ones_like | 根据指定的形状和 dtype创建一个全1数组,one like以另一个数组为参数,并根据其形状和dype创建一个全1数组 |
| zeros,zeros_like | 类似于ones和ones like,只不过产生的是全0数组而已 |
| empty,empty_like | 创建新数组,只分配内存空间但不填充任何值 |
| full,full_like | 用 fill value中的所有值,根据指定的形状和dype创建一个数组,full_like使用另一个数组,用相同的形状和dtype创建 |
| eye,identity | 创建一个正方的NxN单位矩阵(对角线为1,其余为0) |
array()创建是是对原始对象的一份copy创建的,而asarray是当输入是ndarry并不进行复制操作,如果改变创新的数组,则原始数组也会跟着改变。
ndarray的数据类型
dtype(数据类型)是⼀个特殊的对象,它含有ndarray将⼀块内存解释为特定数据类型所需的信息:
简单来说就是==数组元素的类型==.
1 | import numpy as np |
dtype命名规则:
⼀个类型名(如float或int),后⾯跟⼀个⽤于表示各元素位⻓的数字。
标准的双精度浮点值(即Python中的float对象)需要占⽤8字节(即64位)。因此,该类型在NumPy中就记作float64。
使用astype来转化数组的dtype
1 | import numpy as np |
注意,如果将浮点型转化为整形,那么就会截取小数部分:
不管小数部分是什么值,一律舍去
1 | import numpy as np |
字符串类型的数字一样可以转化为数字类型:
1 | import numpy as np |
注意转换的时候可能会发生截取
1 | import numpy as np |
1 | import numpy as np |
NumPy数组的运算
为什么要使用多维数组?
因为这样可以让你不用编写循环就可以对数据执行批量运算.
==运算时,把多维数组当成是矢量.==
⼤⼩相等的数组之间的任何算术运算都会将运算应⽤到元素级:
1 | import numpy as np |
大小相同的数组之间的⽐较会⽣成布尔值数组:
1 | import numpy as np |
不同⼤⼩的数组之间的运算叫做⼴播(broadcasting)
基本的索引和切⽚
1 | import numpy as np |
当你将⼀个标量值赋值给⼀个切⽚时(如arr[5:8]=99),该值会⾃动⼴播到整个选区。
跟列表最重要的区别在于,==数组切片是原始数组的视图==。
这意味着数据不会被复制,==视图上的任何修改都会直接反映到源数组上==。
1 | # arr_slice只是arr的视图而已. |
1 | alist = [1,2,3,4,5,6] |
由于NumPy的设计目的是处理⼤数据,假如NumPy坚持要将数据复制来复制去的话会大量的性能和内存问题。
多维数组的索引问题
- 切片索引:
使用视图 - 布尔索引:
创建数据副本 - 花式索引:
- ⼀次传⼊多个索引数组会返回的⼀个⼀维数组
1 | import numpy as np |
1 | import numpy as np |
1 | import numpy as np |
可以发现,使用索引就能降维(切片不能).
也就是说:arr[1,:2]和arr[1:2,:2]是不一样的
1 | import numpy as np |
现在有7个名字,还有一个7行4列的数据,每个名字对应每一行,现在要找出名字为bob对应的行:
1 | import numpy as np |
注意:布尔型数组的⻓度必须跟被索引的轴⻓度⼀致
(就是这里的7个名字对应7行4列数据)
注意data[names=='Bob',2:]的意义:
选取names==’Bob’的行,再选取2:的列
1 | import numpy as np |
多维数组的否定:
可以使用!=,也可以使用~
1 | import numpy as np |
简单来说:
- &:和
- |:或
- ~:非
1 | import numpy as np |
注意:
- 使用布尔型索引选取数组中的数据,会创建数据的副本
- Python的and和or在布尔型数组中⽆效。要是⽤&与|
布尔型数组的使用:
1 | # 将负值设置为0 |
深入理解广播:
简单来讲,就是所有运算操作,赋值操作,逻辑操作,比较操作等等都会扩散到整个选区
1 | import numpy as np |
1 | import numpy as np |
上面两段代码效果是一样的.一个使用了一次循环,另一个使用了两次循环.
- 代码1的i是对一整行操作.只不过是扩散到那一行的全部元素而已
- 代码2的i是对一个元素的操作,对每个元素都进行了赋值.
reshape函数:
在不改变矩阵的数值的前提下修改矩阵的形状。
1 | import numpy as np |
数组新的shape属性应该要与原来的配套,如果等于-1的话,那么Numpy会根据剩下的维度计算出数组的另外一个shape属性值。
(简单来说,-1代表我不知道要给行(或者列)设置为几,reshape函数会根据原矩阵的形状自动调整。)
1 | import numpy as np |
既然有了reshape,那么构造多维数组就可以使用:
1 | import numpy as np |
花式索引:
利⽤整数数组进⾏索引。
==花式索引跟切⽚不⼀样,它总是将数据复制到新数组中。==
1 | import numpy as np |
注意arr[1,2]和arr[[1,2]]的区别:
arr[1,2]表示选取第一维度中索引值为1的数据,选区第二维度中索引值为2的数据arr[[1,2]]表示选取第一维度中索引值为1和2的数据
简单来说,arr[1,2]是多维度选取,arr[[1,2]]只选择了一个维度
==⼀次传⼊多个索引数组会有⼀点特别。它返回的是⼀个⼀维数组,其中的元素对应各个索引元组==:
1 | import numpy as np |
也就是说:arr[[1,5,7,2],[0,3,1,2]]最终选出的是元素(1,0)、(5,3)、(7,1)和(2,2)。
所以,arr[[1,5,7,2],[1,]]最终选出的是元素(1,1)、(5,1)、(7,1)和(2,1)。
1 | # 花式索引跟切⽚不⼀样,它总是将数据复制到新数组中。 |
重复使用花式索引:
1 | import numpy as np |
数组转置和轴对换:
- 数组转置:
返回源数据的视图(不会进⾏任何复制操作) - 轴对换:
数组转置和内积:
1 | import numpy as np |
内积:
结果数组中的每个元素都是:数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和: **dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])**。
1 | 结果的第一行=arr.T的第一行分别乘以arr的第一列 |
高维数组的转置需要传递一个由轴编号组成的元组,才能进行转置:
1 | import numpy as np |
这⾥,第⼀个轴被换成了第⼆个,第⼆个轴被换成了第⼀个,最后⼀个轴不变。
所谓转置,不过就是进行轴对换而已.所以还有一个swapaxes(交换轴)方法,他需要接受一对轴编号:
1 | import numpy as np |
4.2 通⽤函数:快速的元素级数组函数
通⽤函数可以将其看做简单函数(接受⼀个或多个标量值,并
产⽣⼀个或多个标量值)的⽮量化包装器。
一元ufunc:
1 | import numpy as np |
二元ufunc:
1 | import numpy as np |
ufunc还可以返回多个数组:
1 | import numpy as np |
Ufuncs接受out选项参数,可以让它们在数组的原地进⾏操作:
(提供可选的out参数,并将结果放入给定的输出数组中。 out参数必须是 ndarray 并且具有相同数量的元素。 它可以具有不同的数据类型,在这种情况下将执行转换。)
eg:
ndarray.argmax([axis, out]) 返回给定轴的最大值索引
1 | import numpy as np |
4.3利⽤数组进⾏数据处理
⽤数组表达式代替循环的做法,通常被称为⽮量化。
1 | import numpy as np |
z矩阵上的每一个元素都是sqrt(x^2^+y^2^)的一个解:
1 | 1.41421356就是ys=1,xs=1的解 |
简单来说,首先使用np.meshgrid来构造一个平面点网格(xs,ys)
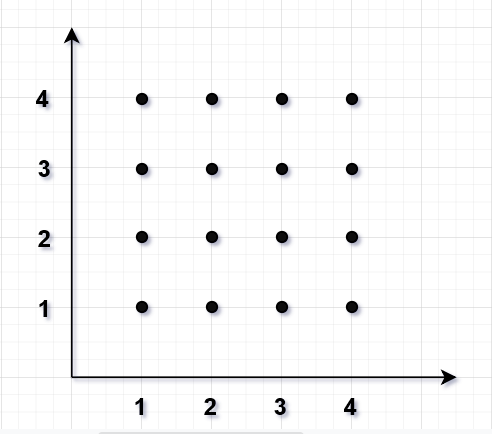
这个网格被拆分成:xs和ys.
然后对于网格的每个点都执行np.sqrt(xs ** 2 + ys ** 2)
最后就得到一个解的矩阵
将条件逻辑表述为数组运算
numpy.where函数是三元表达式x if condition else y的⽮量化版
本。
1 | import numpy as np |
np.where的第⼆个和第三个参数不必是数组,它们都可以是标量值。
np.where通常⽤于根据另⼀个数组⽽产⽣⼀个新的数组。
1 | # 将矩阵的负值改为0,正值不变 |
数学和统计⽅法
mean和sum这类的函数可以接受⼀个axis(轴)选项参数,⽤于计算该轴向上的统计值,最终结果是⼀个少⼀维的数组:
- axis: 不设置值,对全部元素操作
- axis = 0:压缩行,对各列求值,返回 1* n 矩阵
- axis =1 :压缩列,对各行求值,返回 m *1 矩阵
(二维数组就两个轴,所以axis=0/1,三维数组的axis可以等于2,四维数组同理,最高为3)
1 | import numpy as np |
理解什么是axis(轴):
轴即维度,轴的个数被称作rank
(这里的rank不是线性代数中的rank(秩),它指代的依旧是维数(number of dimensions))
1 | import numpy as np |
这里的X.shape为[3, 2, 2],每一个元素就对应一个轴:
- axis=0对应3
- axis=1对应2
- axis=2对应2
对于多维数组,numpy对轴的编号是先行后列,由外向内!
所以:X.sum(axis=0)就是把第一个轴压缩掉.
简单来说,就是==把第一个轴同类的元素全部聚合成一个==
什么是第一个轴同类的元素?
就是==在同一个中括号里面的元素==
累加cumsum/累积cumprod:
1 | import numpy as np |
⽤于布尔型数组的⽅法:
在运算中,布尔值会被强制转换为1和0
1 | import numpy as np |
any和all方法:
和python的any和all方法功能一样:
1 | import numpy as np |
这两个⽅法也能⽤于⾮布尔型数组,所有⾮0元素将会被当做True。
排序
1 | # sort()的参数axis默认为-1 |
将轴编号传给sort(),多维数组就可以在任何⼀个轴向上进⾏排序
1 | import numpy as np |
1 | import numpy as np |
1 | import numpy as np |
上面是对三个轴的排序,解析如下:
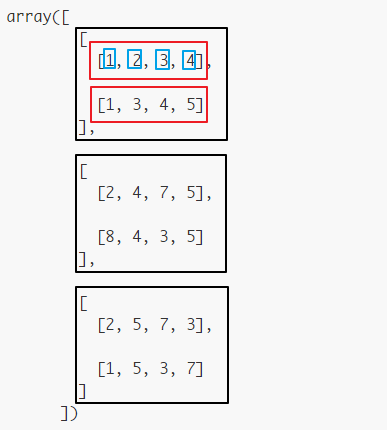
1 | [[[1, 2, 3, 4], |
第一个轴有三个元素:
1
2
3
4
5
6
7
8[[1, 2, 3, 4],
[1, 3, 4, 5],
和
[[2, 4, 7, 5],
[8, 4, 3, 5]],
和
[[2, 5, 7, 3],
[1, 5, 3, 7]]那么这三个元素要排序
所以就是将(1,2,2),(2,4,5),(3,7,7),(3,4,3),(1,8,1),(3,4,5),(4,3,3),(5,5,7)共8组排好.
所以这八组就是(1,2,2),(2,4,5),(3,7,7),(3,3,5),(1,1,8),(3,4,5),(3,3,4),(5,5,7)
对应的矩阵就是:
1
2
3
4
5
6
7
8[[[1 2 3 3]
[1 3 3 5]]
[[2 4 7 4]
[1 4 3 5]]
[[2 5 7 5]
[8 5 4 7]]]
总结:
对于轴的问题,紧抓两个概念:
- 同类元素
- ==多个同类元素最终要变成一个元素==
唯⼀化以及其它的集合逻辑
unique:python里的set的多维数组版
1 | # 唯一化 |
in1d:python里的in的多维数组版
1 | import numpy as np |
4.4⽤于数组的⽂件输⼊输出
NumPy能够读写磁盘上的⽂本数据或⼆进制数据。
np.save和np.load是读写磁盘数组数据的两个主要函数。
默认情况下,数组是以未压缩的原始⼆进制格式保存在扩展名为.npy的⽂件中的:
1 | import numpy as np |
numpy支持将多个数组存储到同一文件中,使用关键字参数标志不同数组:
1 | import numpy as np |
1 | # 读取 |
4.5线性代数
1 | # 前面说过的矩阵内积 |
@符:
进⾏矩阵乘法:
1 | import numpy as np |
1 | import numpy as np |
4.6伪随机数⽣成
1 | import numpy as np |
numpy的伪随机数一样是使用随机种子:
1 | np.random.seed(1234) |
4.7随机漫步:
python实现:
1 | import numpy as np |
numpy实现:
1 | import numpy as np |
产生多个随机漫步过程:
1 | import numpy as np |
计算30或-30的最⼩穿越时间。这⾥稍微复杂些,因为不是5000个过程都到达了30。我们可以⽤any⽅法来对此进⾏检查:
1 | # 每个随机漫步是否抵达30 |
1 | # cleanned_walks:所有到达30的随机漫步的完整数据 |
所以,完整的代码如下:
1 | import numpy as np |