给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。(就是说,在数组中找出两个元素,他们的和为target)
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
1 2 3 给定 nums = [2, 7, 11, 15], target = 9 因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]
最垃圾的算法,复杂度为O(n^2^)
1 2 3 4 5 6 7 8 def twoSum (nums,target ): for index1,num1 in enumerate (nums): for index2,num2 in enumerate (nums): if (index1 != index2) and (num1 + num2 == target): return [index1,index2] a = [2 ,5 ,7 ,9 ] print (func(a,9 ))
正确的实现如下
1 2 3 4 5 6 7 8 9 10 11 def twoSum (nums, target ): hashmap = {} for index, num in enumerate (nums): another_num = target - num if another_num in hashmap: return [hashmap[another_num], index] hashmap[num] = index return None
==经验:下回遇到相加减乘除,都可以考虑移项,使用一个列表或集合将他装起来.==
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
示例 1:
示例 2:
示例 3:
注意:
假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [−2^31^, 2^31^ − 1]。请根据这个假设,如果反转后整数溢出那么就返回 0。
下面是我写的
1 2 3 4 5 6 7 8 9 10 11 class Solution : def reverse (self, x: int ) -> int : if x >0 : temp = int (str (x)[::-1 ]) elif x <0 : temp = - int (str (x)[1 :][::-1 ]) else : return 0 if -2 **31 <temp < 2 **31 -1 : return temp else : return 0
可以更加美观:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution (object def reverse (self, x ): if x < 0 : s = '-' x = -x else : s = '' result = s + str (x)[::-1 ] if int (result) > pow (2 , 31 ) - 1 or int (result) < pow (-2 , 31 ): return 0 return int (result)
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
示例 1:
示例 2:
1 2 3 输入: -121 输出: false 解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
1 2 3 输入: 10 输出: false 解释: 从右向左读, 为 01 。因此它不是一个回文数。
进阶:
你能不将整数转为字符串来解决这个问题吗?
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def isPalindrome (self, x: int ) -> bool : x = str (x) x_half_len = len (x) // 2 if len (x) % 2 == 0 : part1,part2 = x[:x_half_len],x[x_half_len:] else : part1,part2 = x[:x_half_len],x[x_half_len+1 :] if part1 == part2[::-1 ]: return True else : return False
使用算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def isPalindrome (self, x ): temp_x = x k = 0 while temp_x != 0 : k = k * 10 + temp_x % 10 print (k) temp_x = temp_x // 10 if k == x: return True else : return False
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
1 2 3 4 5 6 7 8 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边 。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。 C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
示例 2:
示例 3:
示例 4:
1 2 3 输入: "LVIII" 输出: 58 解释: L = 50, V= 5, III = 3.
示例 5:
1 2 3 输入: "MCMXCIV" 输出: 1994 解释: M = 1000, CM = 900, XC = 90, IV = 4.
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def romanToInt (self, s ): hashmap = {'I' :1 ,'V' :5 ,'X' :10 ,'L' :50 ,'C' :100 ,'D' :500 ,'M' :1000 } result = 0 for i in range (len (s)): if i < len (s)-1 and hashmap[s[i]] < hashmap[s[i+1 ]]: result -= hashmap[s[i]] else : result += hashmap[s[i]] return result
我一开始想的是跳过:当遇到XL,当扫描到X时直接输出90,然后跳过L.
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
1 2 输入: ["flower","flow","flight"] 输出: "fl"
示例 2:
1 2 3 输入: ["dog","racecar","car"] 输出: "" 解释: 输入不存在公共前缀。
说明:
所有输入只包含小写字母 a-z 。
代码如下:
1 2 3 4 5 6 7 8 class Solution : def longestCommonPrefix (self, strs: List [str ] ) -> str : maxStr, minStr = max (strs, default="" ), min (strs, default="" ) for i in range (len (minStr)): if maxStr[i] != minStr[i]: return minStr[:i] return minStr
==经验:==
==如果比较数组for循环的两个each,可以考虑是不是只需比较最长和最短的两个.
==那么如何比较最长和最短的两个,先将他们在for外面取出来,然后在for里使用index,这样就可以使用两个索引来取出这两个值了==
==所以说不要总是想着使用for each in alist,而是使用for index in range(len(alist)-1)==
如果使用二分法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def longestCommonPrefix (self, strs ): if not strs == []: minlen = min ([len (x) for x in strs]) if minlen == 0 : return '' low = 1 high = minlen while low <= high: mid = (low + high) // 2 if self.start_with(strs,mid): low = mid + 1 else : high = mid - 1 return strs[0 ][:min (low,high)] else : return '' def start_with (self,strs,str_len ): word = strs[0 ][:str_len] for each in strs: if not each.startswith(word): return False return True
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
示例 2:
示例 3:
示例 4:
示例 5:
使用栈,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution : def isValid (self,s ): hashmap = {')' :'(' ,']' :'[' ,'}' :'{' } stack = [] if s == '' : return True elif not s[0 ] in ['(' ,'[' ,'{' ]: return False for each in s: if each in ['(' ,'[' ,'{' ]: stack.append(each) else : if stack and stack[-1 ] == hashmap[each]: stack.pop() else : return False if not stack: return True else : return False
还有一种思路:
1 2 3 4 5 6 7 class Solution : def isValid (self, s ): while '{}' in s or '()' in s or '[]' in s: s = s.replace('{}' , '' ) s = s.replace('[]' , '' ) s = s.replace('()' , '' ) return s == ''
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
1 2 输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4
链表定义如下:
1 2 3 4 5 class ListNode : def __init__ (self, x ): self.val = x self.next = None
我的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution : def mergeTwoLists (self, l1: ListNode, l2: ListNode ) -> ListNode: newnode = ListNode(None ) result = newnode while l1 or l2: if l1 and l2: if l1.val >= l2.val: newnode.next = ListNode(l2.val) newnode = newnode.next l2 = l2.next else : newnode.next = ListNode(l1.val) newnode = newnode.next l1 = l1.next elif l1 and (not l2): newnode.next = ListNode(l1.val) newnode = newnode.next l1 = l1.next elif l2 and (not l1): newnode.next = ListNode(l2.val) newnode = newnode.next l2 = l2.next return result.next
==经验:==
==注意13-15行,使用next连接的逻辑:赋值的右边必须新建一个节点==
==必须使用result = newnode来建立一个副本,不然最后return newnode只会返回最后一个节点==
==我们可以在新建ListNode的时候传入一个None作为头节点,最后使用next去除这个头节点==
上面的代码很垃圾,问题出在当其中一个链表不存在的时候,==不需要一个节点一个节点的移动,直接把剩下的链表连接上去就行==
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def mergeTwoLists (self, l1: ListNode, l2: ListNode ) -> ListNode: newnode = ListNode(None ) result = newnode while l1 and l2: if l1.val >= l2.val: newnode.next = ListNode(l2.val) newnode = newnode.next l2 = l2.next else : newnode.next = ListNode(l1.val) newnode = newnode.next l1 = l1.next if l1 and (not l2): newnode.next = l1 elif l2 and (not l1): newnode.next = l2 return result.next
我们根据上面两个代码,总结如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution (object def mergeTwoLists (self, l1, l2 ): dummy = pre = ListNode(0 ) while l1 and l2: if l1.val < l2.val: pre.next = l1 l1 = l1.next else : pre.next = l2 l2 = l2.next pre = pre.next pre.next = l1 or l2 return dummy.next
==注意上面代码的第4行和第14行,是链表最为经常的操作.==
给定一个排序数组,你需要在原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
1 2 3 给定数组 nums = [1,1,2], 函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2:
1 2 3 给定 nums = [0,0,1,1,1,2,2,3,3,4], 函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。 你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用” 方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
1 2 3 4 5 6 7 8 // nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def removeDuplicates (self, nums ): if nums == []:return 0 cur = nums[-1 ] for index in range (len (nums)-2 ,-1 ,-1 ): if cur == nums[index]: nums.pop(index) else : cur = nums[index] return len (nums)
理解第7行的代码,看下面:
1 2 3 4 5 6 7 x = [1 ,2 ,3 ,'?' ,'?' ,'?' ] for each in x[::-1 ]: if each == '?' : x.remove('?' ) print (x)
那个,如果不使用for each in alist,而是使用for index in range呢,该如何倒序:
1 2 3 4 5 6 x = [1 ,2 ,3 ,'?' ,'?' ,'?' ] for index in range (len (x)-1 ,-1 ,-1 ): if x[index] == '?' : x.remove('?' ) print (x)
经验:
==range使用倒序的话,第一参数和第二参数需要互换位置==
原先range的使用规则是for index in range(0,len(alist))
使用for index in range(len(nums)-2,-1,-1)固然可以,可是这时候使用while会更好:
1 2 3 4 5 6 7 def func1 (alist ): i = 0 while i < len (alist): print (alist[i]) i += 1 func1([1 ,2 ,3 ,4 ])
1 2 3 4 5 6 7 def func2 (alist ): i = len (x) - 1 while i >= 0 : print (alist[i]) i -= 1 func2([1 ,2 ,3 ,4 ])
所以代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def removeDuplicates (self, nums ): if nums == []:return 0 cur = nums[-1 ] index = len (nums) - 2 while index >= 0 : if cur == nums[index]: nums.pop(index) else : cur = nums[index] index -= 1 return len (nums)
经验:
给定一个数组 nums 和一个值 val ,你需要原地 移除所有数值等于 val 的元素,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
1 2 3 4 5 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2:
1 2 3 4 5 6 7 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。 注意这五个元素可为任意顺序。 你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用” 方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
1 2 3 4 5 6 7 8 // nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝 int len = removeElement(nums, val); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }
这道题很简单了,使用while循环:
1 2 3 4 5 6 7 8 9 10 class Solution : def removeElement (self,nums,val ): index = len (nums) - 1 while index >= 0 : if nums[index] == val: nums.remove(val) index -= 1 return len (nums)
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1 。
示例 1:
1 2 输入: haystack = "hello", needle = "ll" 输出: 2
示例 2:
1 2 输入: haystack = "aaaaa", needle = "bba" 输出: -1
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义,以及python中的find()相符。
1 2 3 class Solution : def strStr (self, haystack, needle ) -> int : return haystack.find(needle)
自己模拟find函数,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def strStr (self,haystack,needle ): needle_len = len (needle) haystack_len = len (haystack) if needle_len == 0 : return 0 elif haystack_len == 0 : return -1 index = 0 while index <= haystack_len - needle_len: if haystack[index:index + needle_len] == needle: return index index += 1 return -1
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
示例 2:
示例 3:
示例 4:
明显该使用二分法,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def searchInsert (self, nums, target ) -> int : low = 0 high = len (nums) - 1 while low <= high: mid = (low + high) // 2 if target < nums[mid]: high = mid -1 elif target > nums[mid]: low = mid + 1 elif target == nums[mid]: return mid if low > mid: return low else : return high + 1
二分法经验:
==注意第3,4,6行,low=0,high=len(alist)-1,while的判断条件是while low<=high==
==注意最后mid的取值,需要使用if…else语句,而不是直接return min(low,high)==
其实还有一种二分写法:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def searchInsert (self, nums, target ) -> int : low = 0 high = len (nums) while low < high: mid = low + (high - low)//2 if nums[mid] > target: high = mid elif nums[mid] < target: low = mid +1 else : return mid return low
递归的二分法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution (object def searchInsert (self, nums, target ): if len (nums) == 0 : return 0 left = 0 right = len (nums) mid = (left + right) // 2 if mid == left: if nums[mid] < target: return 1 else : return 0 if nums[mid] <= target: return mid + self.searchInsert(nums[mid:],target) else : return self.searchInsert(nums[:mid],target)
报数序列是一个整数序列,按照其中的整数的顺序进行报数,得到下一个数。其前五项如下:
1 2 3 4 5 1. 1 2. 11 3. 21 4. 1211 5. 111221
1 被读作 "one 1" ("一个一") , 即 11。11 被读作 "two 1s" ("两个一"), 即 21。21 被读作 "one 2", “one 1" ("一个二" , "一个一") , 即 1211。
给定一个正整数 n (1 ≤ n ≤ 30),输出报数序列的第 n 项。
注意:整数顺序将表示为一个字符串。
示例 1:
示例 2:
说人话:对序列前一个数进行报数 ,
第一项是一个 1
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def countAndSay (self, n: int ) -> str : param = 1 for _ in range (1 ,n): before = self.get_next(param) param = before return str (param) def get_next (self,before ): before = str (before) cur = before[0 ] count = 1 result = '' for index in range (1 ,len (before)): if cur == before[index]: count += 1 else : result += (str (count) + cur) cur = before[index] count = 1 result += (str (count) + cur) return result
注意上面的5,6,7行代码,这里是不断的执行这个函数.将函数得到的结果当成下一次函数的参数.但是这里并不是递归 .
但是,还是要有这种==在自己的函数体里重复调用别人==的思想.
我还写了个get_before方法:
1 2 3 4 5 6 7 8 9 10 def get_before (after ): after = str (after) result = '' for index in range (0 ,len (after),2 ): result += (int (after[index]) * after[index+1 ]) return int (result) print (get_before(21 )) print (get_before(111221 ))
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
1 2 3 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n ) 的解法,尝试使用更为精妙的分治法求解。
答案代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution (object def maxSubArray (self, nums ): tot = 0 result = nums[0 ] for num in nums: tot += num if tot > result: result = tot if tot < 0 : tot = 0 return result s = Solution() print (s.maxSubArray([-2 ,1 ,-3 ,4 ,-1 ,2 ,1 ,-5 ,4 ]))
代码解释:
1 2 3 对于[-2,1,-3,4,-1,2,1,-5,4]数组来说,扫描-2,小于0.说明-2就是个累赘,舍去. 扫描1时,tot为1,当扫描到-3时,tot=1+(-3)=-2,说明前面的[-2,1,-3]都是没用的. 再次扫描到1时,tot=4-1+2+1=6,当扫描到-5时,tot变成1.此时result跟踪最大值,所以result还是6
所以,还有一种写法:
1 2 3 4 5 6 class Solution (object def maxSubArray (self, nums ): for i in range (1 , len (nums)): nums[i] += max (nums[i-1 ],0 ) return max (nums)
代码解释:
1 2 3 4 5 可以理解为思想是动态规划 nums[i-1]并不是数组前一项的意思,而是到前一项为止的最大子序和 和0比较是因为只要大于0,就可以相加构造最大子序和。如果小于0则相加为0, nums[i] += max(nums[i-1],0)其实是一边遍历一边计算最大序和.也就是说,首先判断i元素前面的子序列有没有用(是否大于0),如果有用的话,就将它们加到i元素上.所以,这个函数会修改原先的nums数组 所以说,在迭代过程中,随着i的增大,只要前面的字序列大于0,i元素的值就会增大.最后使用max找到最大的元素就是我们所求的.
经验:
给定一个仅包含大小写字母和空格 ' ' 的字符串,返回其最后一个单词的长度。
如果不存在最后一个单词,请返回 0 。
说明: 一个单词是指由字母组成,但不包含任何空格的字符串。
示例:
我的代码:
1 2 3 4 5 6 7 8 9 10 class Solution : def lengthOfLastWord (self, s: str ) -> int : if s.find(' ' ) == -1 : return len (s) for each in s.split(' ' )[::-1 ]: if each: return len (each) return 0
如果不使用内置函数,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def lengthOfLastWord (self, s ): cnt = 0 tail = len (s) - 1 while tail >= 0 and s[tail] == ' ' : tail -= 1 while tail >= 0 and s[tail] != ' ' : cnt += 1 tail -= 1 return cnt
经验:
给定一个由整数 组成的非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储一个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
1 2 3 输入: [1,2,3] 输出: [1,2,4] 解释: 输入数组表示数字 123。
示例 2:
1 2 3 输入: [4,3,2,1] 输出: [4,3,2,2] 解释: 输入数组表示数字 4321。
我的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def plusOne (self, digits: List [int ] ) -> List [int ]: digits[-1 ] += 1 idx = len (digits) - 1 while idx > 0 : if digits[idx] == 10 : digits[idx] = 0 digits[idx-1 ] += 1 else : return digits idx -= 1 if digits[0 ] == 10 : digits[0 ] = 0 digits.insert(0 ,1 ) return digits
上面我的代码其实是歪门邪道,真正的做法是设置一个进位标识 (表示是否进位):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def plusOne (self, digits: List [int ] ) -> List [int ]: up = 1 i = 0 while i < len (digits): digits[-1 -i] = (digits[-1 -i] + up ) % 10 if digits[-1 -i] == 0 : up = 1 i += 1 else : break if (i == len (digits) and up == 1 ): digits.insert(0 ,1 ) return digits
经验:
对于进位操作,一般都是:
==使用进位标识==
==while跟踪进位标识==
==当前位的数值为(以前值+进位标识)%进制==
倒序遍历数组有四种方法:
```python
each = ...
1 2 3 4 * ```python for idx in range(len(alist)-1,-1,-1): alist[idx] = ...
```python
alist[idx] = ...
idx -= 1
1 2 3 4 5 6 * ```python idx = 0 while idx < len(alist): alist[-1-idx] = ... idx += 1
给定两个二进制字符串,返回他们的和(用二进制表示)。
输入为非空 字符串且只包含数字 1 和 0。
示例 1:
1 2 输入: a = "11", b = "1" 输出: "100"
示例 2:
1 2 输入: a = "1010", b = "1011" 输出: "10101"
如果使用内置函数int:
1 2 3 class Solution : def addBinary (self, a: str , b: str ) -> str : return bin (int (a,2 ) + int (b,2 ))[2 :]
要使用上面说的进位标志,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def addBinary (self, a: str , b: str ) -> str : if len (a) > len (b): b = '0' *int (len (a)-len (b)) + b else : a = '0' *int (len (b)-len (a)) + a up = 0 res = '' idx = len (a) - 1 while idx >= 0 : quo,remain = divmod (int (a[idx])+int (b[idx])+up,2 ) res = str (remain) + res if quo > 0 : up = 1 else : up = 0 idx -= 1 if up == 1 : res = '1' + res return res
上面使用了quo,remain = divmod(int(a[idx])+int(b[idx])+up,2),但是注意到quo不是1就是0,和up是完全一样的值,所以可以直接使用up来代替quo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def addBinary (self, a: str , b: str ) -> str : if len (a) > len (b): b = '0' *int (len (a)-len (b)) + b else : a = '0' *int (len (b)-len (a)) + a up = 0 res = '' idx = len (a) - 1 while idx >= 0 : up,remain = divmod (int (a[idx])+int (b[idx])+up,2 ) res = str (remain) + res idx -= 1 if up == 1 : res = '1' + res return res
经验:
==quo,remain = divmod((string1[idx] + string2[idx] + up) ,进制)==,如果quo==1,就说明发生了进位.
当前值==s=(string1[idx] + string2[idx] + up) % 进制==,如果string[idx]+strings[idx]+up>进制,就说明发生了进位
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
示例 2:
1 2 3 输入: 8 输出: 2 说明: 8 的平方根是 2.82842...由于返回类型是整数,小数部分将被舍去。
当然可以使用遍历,但是复杂度高:
1 2 3 4 5 class Solution : def mySqrt (self, x: int ) -> int : for each in range (x+1 ): if each**2 <= x < (each+1 )**2 : return each
我的代码:使用二分法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def mySqrt (self, x: int ) -> int : low = 0 high = x while low <= high: mid = (low + high) // 2 if mid**2 <= x <= (mid+1 )**2 : if not (mid+1 )**2 == x: return mid else : return mid + 1 elif mid**2 < x: low = mid + 1 elif mid**2 > x: high = mid - 1 return mid
经验:
BC段:对应第9行代码的if
AB段:对应第14行代码的if
CD段:对应第16行代码的if
1 2 3 4 graph LR; A --> B; B --> C; C --> D;
一般来说,会==优先处理中间段(BC),BC长度固定为1,并且BC段会包含两个端点==,这样就能有效的防止low = mid + 1,high = mid - 1超出界限.
回顾地35题(搜索插入顺序)也是二分法,因为数组元素之间的距离就是为1,所以我们不必担心low = mid + 1,high = mid - 1会超出界限.
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意: 给定 n 是一个正整数。
示例 1:
1 2 3 4 5 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
1 2 3 4 5 6 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
设$x$为1阶的数量,$y$为2阶的数量,$n$为总阶数.
我的思路:
因为一阶的数量为$x$,二阶的数量为$y$,所以数量和为$x+y$,即$n-y$
题目可以演变成:
因为当$y=0$的时候,只有一种方案,所以总数量要加1
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def fact (self,n ): res = 1 for each in range (2 ,n+1 ): res *= each return res def combo (self,m,n ): return int (self.fact(n)/(self.fact(m)*self.fact(n-m))) def climbStairs (self, n: int ) -> int : res = 0 for y in range (1 ,n//2 +1 ): res += self.combo(y,n-y) return res + 1
其实如果多列几项的话,就可以看出规律了:
1 2 3 4 5 6 一阶楼梯:1 两阶楼梯:2 三阶楼梯:3 四阶楼梯:5 五阶楼梯:8 六阶楼梯:13
实际就是一个缺少第一项的斐波那契数列,具体思路:
1 n个台阶,一开始可以爬 1 步,也可以爬 2 步,那么n个台阶爬楼的爬楼方法就等于一开始爬1步的方法数 + 一开始爬2步的方法数,这样我们就只需要计算n-1个台阶的方法数和n-2个台阶方法数
所以可以这么写:
1 2 3 4 5 6 7 8 9 10 11 12 from functools import lru_cacheclass Solution : @lru_cache(10 **8 def climbStairs (self, n ): if n == 1 : return 1 elif n == 2 : return 2 else : return self.climbStairs(n - 1 ) + self.climbStairs(n - 2 )
我们可以手动设置存缓:
1 2 3 4 5 6 7 8 9 10 11 class Solution : def climbStairs (self, n ): cache = {} cache[0 ] = 1 cache[1 ] = 1 cache[2 ] = 2 for i in range (2 ,n+1 ): cache[i] = cache[i-1 ] + cache[i-2 ] return cache[i]
上面的抖机灵算法,其实是一个动态规划 问题,
==一个问题可以通过更小子问题的解决方法来解决==(即问题的最优解 包含了其子问题的最优解,也就是最优子结构性质 )。
有些子问题的解可能需要计算多次(也就是子问题重叠性质 )。
子问题的解存储在一张表格里,这样每个子问题只用计算一次。
需要额外的空间以节省时间。
给定一个排序链表,删除所有重复的元素,使得每个元素只出现一次。
示例 1:
示例 2:
1 2 输入: 1->1->2->3->3 输出: 1->2->3
链表的定义如下:
1 2 3 4 5 class ListNode : def __init__ (self, x ): self.val = x self.next = None
我写的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def deleteDuplicates (self, head: ListNode ) -> ListNode: if not head: return None elif not head.next : return head dummy = pre = head after = pre.next while after.next : if pre.val == after.val: pre.next = after.next after = pre.next else : pre = after after = after.next if pre.val == after.val: pre.next = None return dummy
其实after不是必须的,可以使用pre.next代替,修改之后代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution : def deleteDuplicates (self, head: ListNode ) -> ListNode: if (not head) or (not head.next ): return head dummy = pre = head while pre.next .next : if pre.val == pre.next .val: pre.next = pre.next .next else : pre = pre.next if pre.val == pre.next .val: pre.next = None return dummy
上面代码分类太多了,应该如下使用:
1 2 3 4 5 6 7 8 9 class Solution : def deleteDuplicates (self, head: ListNode ) -> ListNode: c = head while (head!=None and head.next !=None ): if head.next .val == head.val: head.next = head.next .next else : head = head.next return c
比较两种方法,得出经验:
给定两个有序整数数组 nums1 和 nums2 ,将 nums2 合并到 nums1 中, 使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n )来保存 nums2 中的元素。
示例:
1 2 3 4 输入: nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3 输出: [1,2,2,3,5,6]
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def merge (self, nums1, m, nums2, n ): while n and m: if nums2[n-1 ] >= nums1[m-1 ]: nums1[n+m-1 ] = nums2[n-1 ] n -= 1 else : nums1[n+m-1 ] = nums1[m-1 ] m -= 1 for i in range (n): nums1[i] = nums2[i]
同样的逻辑,上面代码可以修改为两个while:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def merge (self,num1,m,num2,n ): p = m + n -1 m = m- 1 n = n - 1 while (m>=0 and n >=0 ): if (num1[m] > num2[n]): num1[p] = num1[m] m = m -1 p = p-1 else : num1[p] = num2[n] n = n -1 p = p-1 while (n>=0 ): num1[p] = num2[n] n = n -1 p = p-1 return None
将两个while合起来,可以得到最终代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution (object def merge (self, nums1, m, nums2, n ): merge_index = m + n - 1 index1 = m - 1 index2 = n - 1 while index1 >= 0 or index2 >= 0 : if index1 < 0 : nums1[merge_index] = nums2[index2] index2 = index2 - 1 elif index2 < 0 : nums1[merge_index] = nums1[index1] index1 = index1 - 1 elif nums1[index1] > nums2[index2]: nums1[merge_index] = nums1[index1] index1 = index1 - 1 else : nums1[merge_index] = nums2[index2] index2 = index2 - 1 merge_index = merge_index - 1
这其实是==归并排序的最后一并==.
这里顺便回顾一下归并排序:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 def mergeSort (alist ): print ("Splitting " ,alist) if len (alist)>1 : mid = len (alist)//2 lefthalf = alist[:mid] righthalf = alist[mid:] mergeSort(lefthalf) mergeSort(righthalf) i=j=k=0 while i < len (lefthalf) and j < len (righthalf): if lefthalf[i] < righthalf[j]: alist[k]=lefthalf[i] i=i+1 else : alist[k]=righthalf[j] j=j+1 k=k+1 while i < len (lefthalf): alist[k]=lefthalf[i] i=i+1 k=k+1 while j < len (righthalf): alist[k]=righthalf[j] j=j+1 k=k+1 print ("Merging " ,alist) alist = [54 ,26 ,93 ,17 ,77 ,31 ,44 ,55 ,20 ] mergeSort(alist) print (alist)
结果为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Splitting [54, 26, 93, 17, 77, 31, 44, 55, 20] Splitting [54, 26, 93, 17] Splitting [54, 26] Splitting [54] Merging [54] Splitting [26] Merging [26] Merging [26, 54] Splitting [93, 17] Splitting [93] Merging [93] Splitting [17] Merging [17] Merging [17, 93] Merging [17, 26, 54, 93] Splitting [77, 31, 44, 55, 20] Splitting [77, 31] Splitting [77] Merging [77] Splitting [31] Merging [31] Merging [31, 77] Splitting [44, 55, 20] Splitting [44] Merging [44] Splitting [55, 20] Splitting [55] Merging [55] Splitting [20] Merging [20] Merging [20, 55] Merging [20, 44, 55] Merging [20, 31, 44, 55, 77] Merging [17, 20, 26, 31, 44, 54, 55, 77, 93] [17, 20, 26, 31, 44, 54, 55, 77, 93]
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
1 2 3 4 5 6 输入: 1 1 / \ / \ 2 3 2 3 [1,2,3], [1,2,3] 输出: true
示例 2:
1 2 3 4 5 6 输入: 1 1 / \ 2 2 [1,2], [1,null,2] 输出: false
示例 3:
1 2 3 4 5 6 输入: 1 1 / \ / \ 2 1 1 2 [1,2,1], [1,1,2] 输出: false
我的代码(是错误的):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def preorder (self,node ): if node.left: return self.preorder(node.left) else : return node.val if node.right: return self.preorder(node.right) else : return node.val def isSameTree (self, p: TreeNode, q: TreeNode ) -> bool : if not p or not q: if p == q: return True else : return False if p.val == q.val: return self.preorder(p) == self.preorder(q) else : return False
上面代码在输入为[10,5,15],[10,5,null,null,15]的时候,是错的.程序会返回True而不是False.
经验:==如果需要递归比较,那么就该递归参数必须含有这两个参数,不能在递归函数外比较==
递归的基线条件:
两个节点都为空
一个为空,另一个非空
都为非空,但是值不相等
递归条件:都为非空,但是值相等.
输入的明显是前序遍历,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def isSameTree (self, p, q ): if not p and not q: return True elif p and q : if p.val == q.val: return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right) else : return False else : return False
注意第10行:==需要使用and,左边判断两棵树的左子树是否相等,右边判断右子树是否相等==
可以更加精简:
1 2 3 4 5 6 7 8 class Solution : def isSameTree (self, p: TreeNode, q: TreeNode ) -> bool : if p and q and p.val==q.val: return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right) if not p: return not q return False
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 2 3 4 5 1 / \ 2 2 / \ / \ 3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
说明:
如果你可以运用递归和迭代两种方法解决这个问题,会很加分。
==其实对称就是左子树等于右子树==,这里可以稍微修改一下100题的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def isSymmetric (self, root: TreeNode ) -> bool : def isSame (p,q ): if p and q and p.val==q.val: return isSame(p.left,q.right) and isSame(p.right,q.left) if not p: return not q return False if not root: return True return isSame(root.left,root.right)
同理,可以设计一个isMorror函数:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution (object def isSymmetric (self, root ): return self.isMirror(root,root) def isMirror (self,t1,t2 ): if not t1 and not t2: return True elif not t1 or not t2: return False return t1.val==t2.val and self.isMirror(t1.right,t2.left) and self.isMirror(t1.left,t2.right)
上面都是递归实现,可以使用中序遍历实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution (object def isSymmetric (self, root ): if root: return self.is_mirror(root.left, root.right) return True def is_mirror (self, l_root, r_root ): if l_root and r_root: if self.is_mirror(l_root.left, r_root.right): if l_root.val == r_root.val: return self.is_mirror(l_root.right, r_root.left) return False return l_root == r_root
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: [3,9,20,null,null,15,7],
返回它的最大深度 3 。
代码如下:
1 2 3 4 5 6 7 8 9 class Solution (object def maxDepth (self, root ): if not root: return 0 lep = self.maxDepth(root.left) rep = self.maxDepth(root.right) return max (lep,rep)+1
经验:
==使用递归的时候一定要搞清楚这个递归函数是干什么的,不然就不知道什么时候使用这个函数==.(就像对称二叉树题目的is_mirror函数和相同的树题目中的isSameTree函数)
树递归的基线条件一般是==到达叶节点==
==在递归中,需要需要计数,那么就计数的变量return出来.就是说:递归函数求什么就需要return出什么==
(重要)==使用递归时,不要管多层的递归栈,只要满足递归条件,只考虑一层栈即可.==
总结使用递归时的思路:
确定基线条件和递归条件
每次递归都要缩小问题的的规模,不断向基线条件靠拢
不过递归的多深,迟早是要return的
(重要)==使用递归时,不要管多层的递归栈,只要满足递归条件,只考虑一层栈即可,使用递归的时候一定要搞清楚这个递归函数是干什么的,不然就不知道什么时候使用这个函数.==
==在递归中,需要需要计数,那么就计数的变量return出来.==
带着这五个点来看上面的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def maxDepth (self, root ): if not root: return 0 lep = self.maxDepth(root.left) rep = self.maxDepth(root.right) return max (lep,rep)+1
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:[3,9,20,null,null,15,7],
返回其自底向上的层次遍历为:
1 2 3 4 5 [ [15,7], [9,20], [3] ]
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution : def levelOrderBottom (self, root: TreeNode ) -> List [List [int ]]: if not root: return [] stack = [root] res = [] while len (stack) != 0 : tmp = [] res_each = [] for i in stack: res_each.append(i.val) if i.left: tmp.append(i.left) if i.right: tmp.append(i.right) stack = tmp res.insert(0 ,res_each) return res
也可以使用队列:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution (object def levelOrderBottom (self, root ): if not root: return [] return self.levelOrder(root) def levelOrder (self,root ): q = deque() q.append(root) List = [] while q: res = [] for i in range (len (q)): item = q.popleft() res.append(item.val) if item.left: q.append(item.left) if item.right: q.append(item.right) List .append(res) output = [] while (List ): output.append(List .pop()) return output
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
1 2 3 4 5 6 7 8 9 给定有序数组: [-10,-3,0,5,9], 一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树: 0 / \ -3 9 / / -10 5
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution (object def sortedArrayToBST (self, nums ): if len (nums)==0 : return None if len (nums)==1 : return TreeNode(nums[0 ]) mid = int (len (nums)//2 ) root = TreeNode(nums[mid]) root.left = self.sortedArrayToBST(nums[:mid]) root.right = self.sortedArrayToBST(nums[mid+1 :]) return root
经验:
==列表的基线条件不仅可以用for each in alist,还可以不断的二分来获取,这时候的递归参数基本就是alist[:mid]和alist[:mid+1]==
涉及列表和树,基本不会使用for each in alist.因为需要root = TreeNode来创建节点.
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1 2 3 4 5 6 7 1 / \ 2 2 / \ 3 3 / \ 4 4
返回 false 。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def isBalanced (self, root: TreeNode ) -> bool : if not root: return True if abs (self.countfloor(root.left)-self.countfloor(root.right))>1 : return False else : return self.isBalanced(root.left) and self.isBalanced(root.right) def countfloor (self,root ): if not root: return 0 else : return max (self.countfloor(root.left),self.countfloor(root.right))+1
我的代码(是错误的):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def get_height (self,root ): if not root: return 0 a = self.get_height(root.left) + 1 b = self.get_height(root.right) + 1 return max (a,b) def isBalanced (self, root: TreeNode ) -> bool : if not root: return True a = self.get_height(root.left) b = self.get_height(root.right) if abs (a-b) <= 1 : return True else : return False
上面正确的代码和我的代码最大的区别就是最后的return:
经验:==需要对整个树的节点都使用递归函数,那么就需要对Node.left和Node.right使用该递归函数==
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
返回它的最小深度 2.
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def minDepth (self, root: TreeNode ) -> int : if not root: return 0 a = self.minDepth(root.left) b = self.minDepth(root.right) if not root.left or not root.right: return 1 + max (a,b) else : return 1 + min (a,b)
经验:==在递归中,判断叶节点的方式有两种==
if not root.left or not root.right:if not root
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: sum = 22,
1 2 3 4 5 6 7 5 / \ 4 8 / / \ 11 13 4 / \ \ 7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def hasPathSum (self, root, sum ): if not root: return False if sum == root.val and not root.left and not root.right: return True if self.hasPathSum(root.left,sum -root.val) or self.hasPathSum(root.right,sum -root.val): return True else : return False
这里的递归条件是==节点的左子树或者右子树的路径和是sum-root.val==
经验:
==递归里的加法我们可以让参数递减来实现==
我们在写递归代码的时候一定要注意描述出递归条件
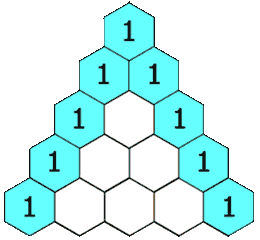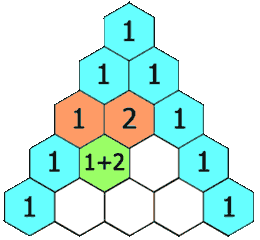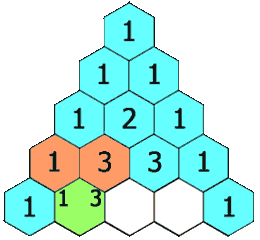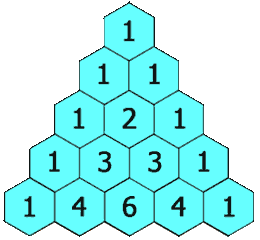
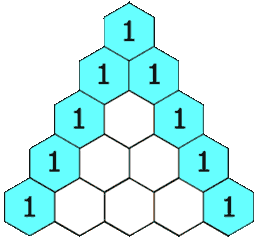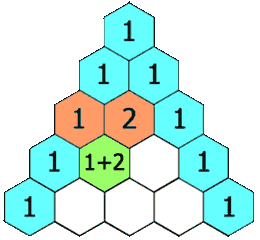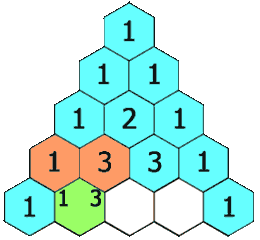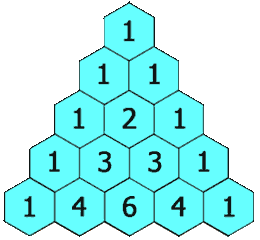
给定一个非负整数 numRows, 生成杨辉三角的前 numRows 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
1 2 3 4 5 6 7 8 9 输入: 5 输出: [ [1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1] ]
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def triangle (self, numRows ): if numRows == 0 : return [] elif numRows == 1 : return [1 ] else : a = self.triangle(numRows-1 ) return [1 ] + [a[n]+a[n+1 ] for n in range (len (alist)-1 )] + [1 ] def generate (self,numRows ): return [self.triangle(num) for num in range (1 ,numRows+1 )]
经验:==一旦求了通项函数,要求遍历的值.这时需要果断新建一个函数进行遍历==
当然可以使用循环来解决:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def generate (self, numRows ): result = [] for i in range (numRows): now = [1 ]*(i+1 ) if i >= 2 : for n in range (1 ,i): now[n] = pre[n-1 ]+pre[n] result += [now] pre = now return result
给定一个非负索引 k ,其中 k ≤ 33,返回杨辉三角的第 k 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
进阶:
你可以优化你的算法到 O (k ) 空间复杂度吗?
我的代码:刚刚已经求出通项函数了,现在直接套用:
1 2 3 4 5 6 7 8 9 class Solution : def getRow (self, rowIndex: int ) -> List [int ]: return self.triangle(rowIndex+1 ) def triangle (self, rowIndex: int ) -> List [int ]: if rowIndex == 1 : return [1 ] else : a = self.triangle(rowIndex-1 ) return [1 ] + [a[n]+a[n+1 ] for n in range (len (alist)-1 )] + [1 ]
也可以使用循环:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def getRow (self, rowIndex ): re = [1 ]+[0 ]*(rowIndex) for i in range (1 ,rowIndex+1 ): re[i] = 1 for j in range (i-1 , 0 , -1 ): re[j] += re[j-1 ] return re
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
1 2 3 输入: [7,1,5,3,6,4] 输出: 5 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
1 2 3 输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
我的代码:和53题”求最大子序列和”一样的思路.是一个动态规划问题:前i天的最大收益 = max{前i-1天的最大收益,第i天的价格-前i-1天中的最小价格}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def maxProfit (self, prices: List [int ] ) -> int : if not prices: return 0 res = 0 buy = prices[0 ] idx = 1 while idx <= len (prices)-1 : if buy - prices[idx] > 0 : buy = prices[idx] elif -(buy - prices[idx]) > res: res = -(buy - prices[idx]) idx += 1 return res
真正的动态规划写法:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def maxProfit (self, prices ): min_p = float ('inf' ) res = 0 for i in range (len (prices)): min_p = min (min_p, prices[i]) res = max (res, prices[i] - min_p) return res
对比上面两种代码,其实是一致的:
1 2 3 4 5 6 7 8 9 10 11 12 13 if buy - prices[idx] > 0 : buy = prices[idx] elif -(buy - prices[idx]) > res: res = -(buy - prices[idx]) min_p = min (min_p, prices[i]) res = max (res, prices[i] - min_p)
回忆53题”求最大子序列和”的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution (object def maxSubArray (self, nums ): tot = 0 res = nums[0 ] idx = 1 while idx <= len (nums)-1 : tot += nums[idx] res = max (res,tot) tot = max (tot,0 ) idx += 1 return res class Solution (object def maxSubArray (self, nums ): tot = 0 result = nums[0 ] for num in nums: tot += num if tot > result: result = tot if tot < 0 : tot = 0 return result
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
1 2 3 输入: [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
1 2 3 输入: [1,2,3,4,5] 输出: 4 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
1 2 3 输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
[7, 1, 5, 6] 第二天买入,第四天卖出,收益最大(6-1),所以**一般人可能会想,怎么判断不是第三天就卖出了呢? **这里就把问题复杂化了.
代码如下:
1 2 3 4 5 6 7 8 9 class Solution (object def maxProfit (self, prices ): profit = 0 for day in range (len (prices)-1 ): differ = prices[day+1 ] - prices[day] if differ > 0 : profit += differ return profit
还有一种非常装逼的写法:
1 2 3 class Solution (object def maxProfit (self, prices ): return sum (b-a for a,b in zip (prices,prices[1 :]) if b>a)
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明: 本题中,我们将空字符串定义为有效的回文串。
示例 1:
1 2 输入: "A man, a plan, a canal: Panama" 输出: true
示例 2:
1 2 输入: "race a car" 输出: false
代码:
1 2 3 4 class Solution : def isPalindrome (self, s ): s = '' .join(filter (str .isalnum,s)).lower() return s==s[::-1 ]
Python isalnum() 方法检测字符串是否由字母和数字组成。
类似函数:
str.isalnum() 函数:判断该字符串是否只是字母数字组合
str.isalpha() 函数:判断该字符串是否是字母组合
str.isdigit() 函数:判断该字符串是否只包含数字
str.islower() 函数:判断该字符串中是否只是小写字母
str.isupper() 函数:检查该字符串中的单词是否首字母都大写
str.isspace() 函数:判断该字符串是否只包含空格
str.istitle() 函数:检查该字符串中的单词是否首字母都大写
当然,可以使用双指针:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution (object def isPalindrome (self, s ): s_length = len (s) if s_length <= 1 : return True i = 0 j = s_length - 1 while i <= j: while not s[i].isalnum() and i < j: i += 1 while not s[j].isalnum() and i < j: j -= 1 if s[i].lower() != s[j].lower(): return False else : i += 1 j -= 1 return True
经验:==对于类似于回文问题,不要使用二分法,而是使用双指针==
1 2 3 4 5 6 7 8 9 10 11 12 def shuanzhizhen (string ): left = 0 right = len (string) - 1 while left <= right: if string[left] != string[right]: return False left += 1 right -= 1 return True print (shuanzhizhen('123456654321' ))
给定一个非空 整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
示例 2:
代码如下:
1 2 3 4 5 6 7 class Solution : def singleNumber (self, nums ): a = 0 for num in nums: a = a ^ num return a
异或复习:
1 2 3 4 5 交换律:a ^ b ^ c <=> a ^ c ^ b 任何数于0异或为任何数 0 ^ n => n 相同的数异或为0: n ^ n => 0 所以,对于var a = [2,3,2,4,4]: 2 ^ 3 ^ 2 ^ 4 ^ 4等价于 2 ^ 2 ^ 4 ^ 4 ^ 3 => 0 ^ 0 ^3 => 3
还有讨巧的方法:
1 2 3 class Solution : def singleNumber (self, nums ): return 2 *sum (set (nums)) - sum (nums)
或者:
1 2 3 4 5 class Solution (object def singleNumber (self, nums ): for i in nums: if nums.count(i) == 1 : return i
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
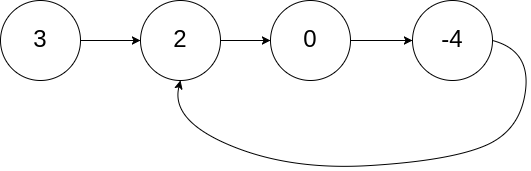
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
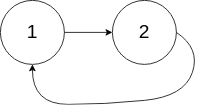
1 2 3 输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
1 2 3 输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
进阶:
你能用 *O(1)*(即,常量)内存解决此问题吗?
有一种调皮的算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution (object def hasCycle (self, head ): while head: if head.val == 'bjfuvth15925' : return True else : head.val = 'bjfuvth15925' head = head.next return False
最准确的做法:使用快慢双指针
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution (object def hasCycle (self, head ): if not head or not head.next : return False slow = fast = head while fast.next and fast.next .next : slow = slow.next fast = fast.next .next if slow == fast: return True return False
快慢双指针的内存就是$$O(1)$$
用一个更好理解的版本:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution (object def hasCycle (self, head ): slow = fast = head while slow and fast: if slow.next : slow = slow.next fast = fast.next if fast: fast = fast.next if slow == fast: return True return False
可以使用地址法:
1 2 3 4 5 6 7 8 9 10 class Solution (object def hasCycle (self, head ): id_list = [] while head: if not id (head) in id_list: id_list.append(id (head)) head = head.next else : return True return False
经验:==对于环的判断,要使用快慢指针==
设计一个支持 push,pop,top 操作,并能在常数时间 内检索到最小元素的栈。
push(x) – 将元素 x 推入栈中。
pop() – 删除栈顶的元素。
top() – 获取栈顶元素。
getMin() – 检索栈中的最小元素。
示例:
1 2 3 4 5 6 7 8 MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
就是普通的stack多了一个getMin()函数.
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class MinStack (object def __init__ (self ): self.stack = [] self.minstack = [] def push (self, x ): self.stack.append(x) if self.minstack == [] or x <= self.minstack[-1 ]: self.minstack.append(x) def pop (self ): if self.stack: if self.stack[-1 ] == self.minstack[-1 ]: self.minstack.pop() self.stack.pop() def top (self ): if self.stack: return self.stack[-1 ] def getMin (self ): if self.minstack: return self.minstack[-1 ]
测试:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 minstack = MinStack() minstack.push(5 ) minstack.push(3 ) minstack.push(4 ) minstack.push(1 ) minstack.push(2 ) print (minstack.stack,minstack.minstack) print (minstack.getMin()) minstack.pop() print (minstack.getMin()) minstack.pop() print (minstack.getMin()) minstack.pop() print (minstack.getMin())
注意上面代码的10,11行:
1 2 if self.minstack == [] or x <= self.minstack[-1 ]: self.minstack.append(x)
minstack.minstack并没有维护整个排好序的stack,minstack.minstack只是维护了降序的stack :x <= self.minstack[-1]保证了最小值一定在最后,self.minstack == []保证了stack栈底元素一定在最前.
这样就导致了在stack中,比minstack最小元素还要小的元素一定排在前面,会更早的被pop出来 .eg:上面测试中,4并没有在minstack中.但是在stack中4排在3的前面,也就是说==如果要pop出3一定要先pop出4==
经验:==以空间换时间的做法就是维护一个数据来存放必要的东西==
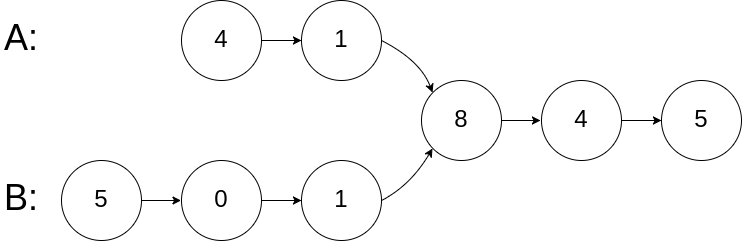
编写一个程序,找到两个单链表相交的起始节点。
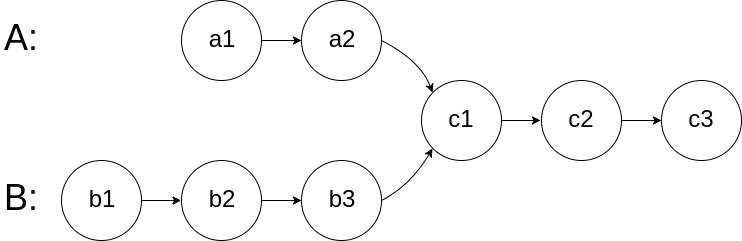
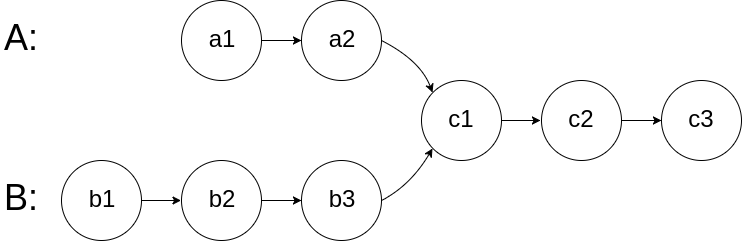
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
1 2 3 输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Reference of the node with value = 8 输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
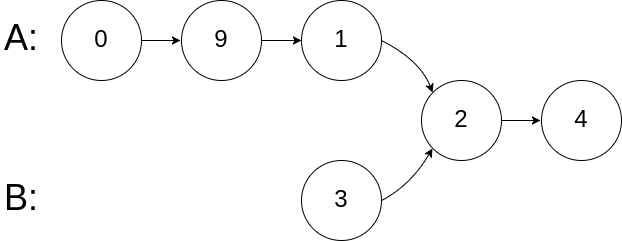
1 2 3 输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Reference of the node with value = 2 输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
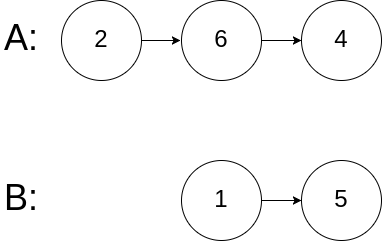
1 2 3 4 输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n ) 时间复杂度,且仅用 O(1 ) 内存。
最简单的想法就是使用地址法:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution (object def getIntersectionNode (self, headA, headB ): id_list = [] while headA: id_list.append(id (headA)) headA = headA.next while headB: if id (headB) in id_list: return headB headB = headB.next return None
链表相交使用==双指针法==:定义两个指针, 第一轮让两个到达末尾的节点指向另一个链表的头部, 最后如果相遇则为交点 (这移动中恰好抹除了长度差) 两个指针等于移动了相同的距离, 有交点就返回, 无交点就是各走了两条指针的长度
理解:
在相交前,
代码如下:
1 2 3 4 5 6 7 8 class Solution (object def getIntersectionNode (self, headA, headB ): a, b = headA, headB while a != b: a = a.next if a else headB b = b.next if b else headA return a
当然可以写的罗嗦一点:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution (object def getIntersectionNode (self, headA, headB ): if not headA or not headB: return p = headA q = headB flag = 0 while p != q and flag <= 2 : if not p: p = headB flag += 1 else : p = p.next if not q: q = headA flag += 1 else : q = q.next if p == q: return p return
还可以使用快慢指针:
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution (object def getIntersectionNode (self, headA, headB ): a = headA b = headB a_num = b_num = 0 while a: a = a.next a_num += 1 while b: b = b.next b_num += 1 if a_num >= b_num: gap = a_num - b_num while gap: headA = headA.next gap -= 1 while headA and headB: if headA == headB: return headA headA = headA.next headB = headB.next return else : gap = b_num - a_num while gap: headB = headB.next gap -= 1 while headA and headB: if headA == headB: return headA headA = headA.next headB = headB.next return
相同的逻辑,上面的写法太罗嗦,下面的优雅很多:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution (object def getIntersectionNode (self, headA, headB ): a,b = 0 ,0 p,q = headA,headB while headA and headB: headA = headA.next headB = headB.next a += 1 b += 1 while headA: headA = headA.next p = p.next while headB: headB = headB.next q = q.next while p: if p == q: return p p = p.next q = q.next return
经验:对于相交链表,有两种方式:
==快慢指针==:求出两个链表A和B的长度, 长链表先走|len(A)-len(B)|步, 然后同时遍历返回第一个公共节点.
==指针追逐==:定义两个指针, 第一轮让两个到达末尾的节点指向另一个链表的头部, 最后如果相遇则为交点.
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
1 2 3 输入: numbers = [2, 7, 11, 15], target = 9 输出: [1,2] 解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
采用前后双指针法:小了往后走 大了往前走
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def twoSum (self, numbers, target ): left = 0 right = len (numbers) - 1 while left < right: cur = numbers[left] + numbers[right] if cur < target: left += 1 elif cur > target: right -= 1 elif cur == target: return left+1 ,right+1
给定一个正整数,返回它在 Excel 表中相对应的列名称。
例如,
1 2 3 4 5 6 7 8 1 -> A 2 -> B 3 -> C ... 26 -> Z 27 -> AA 28 -> AB ...
示例 1:
示例 2:
示例 3:
本质相当于26进制,转换前需减1 ,代码如下:
1 2 3 4 5 6 7 8 def convertToTitle (self, n ): res = '' while n > 0 : n,remain = divmod (n-1 ,26 ) res = chr (65 + remain) + res return res
也可以使用递归:
1 2 3 4 5 6 7 class Solution : def convertToTitle (self, n ): if (n-1 )//26 == 0 : return chr ( 65 + (n-1 ) % 26 ) else : return self.convertToTitle( (n-1 )//26 ) + chr (65 + (n-1 ) % 26 )
经验:
==对于禁止转化,注意要减一==
对于数字转字母,注意不要使用字典去映射,直接使用chr函数.
给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在众数。
示例 1:
示例 2:
1 2 输入: [2,2,1,1,1,2,2] 输出: 2
最简单的方式就是使用字典了:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution (object def majorityElement (self, nums ): hashmap = {} for num in nums: if num in hashmap: hashmap[num] += 1 else : hashmap[num] = 1 for key,val in hashmap.items(): if val > len (nums)//2 : return key
更合适的做法是:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def majorityElement (self, nums ): cnt, ret = 0 , 0 for num in nums: if cnt == 0 : ret = num if num != ret: cnt -= 1 else : cnt += 1 return ret
摩尔投票算法:超过$\frac{1}{K}$ (即大于$\frac{n}{K}$次)的元素(假设满足要求的元素存在)。满足要求的元素最多有$(k−1)$个。
摩尔投票算法可以快速的计算出一个数组中出现次数过半的数即大多数(majority) ,算法核心思想是同加,异减
该方法的思想是众数一定比其他所有的数加起来的数量要多,就算是众数与其他每一个数相抵消,最后剩下来的也是众数。况且还有其他数之间的抵消,所以剩下来的一定是众数。
当K大于2的时候,代码会比较复杂:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution (object def majorityElement (self, nums ): a, b, ca, cb = None , None , 0 , 0 for num in nums: if num == a: ca += 1 elif num == b: cb += 1 elif ca == 0 : a, ca = num, 1 elif cb == 0 : b, cb = num, 1 else : ca -= 1 cb -= 1 ca, cb = 0 , 0 for num in nums: if num == a: ca += 1 elif num == b: cb += 1 ans = [] if ca > len (nums)//3 : ans.append(a) if cb > len (nums)//3 : ans.append(b) return ans
经验:对于出现次数大于$\frac{1}{K}$的情况,可以使用==摩尔投票法==
给定一个Excel表格中的列名称,返回其相应的列序号。
例如,
1 2 3 4 5 6 7 8 A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ...
示例 1:
示例 2:
示例 3:
我的代码如下:
1 2 3 4 5 6 7 8 9 10 class Solution (object def titleToNumber (self, s ): up = 1 res = 0 for each in s[::-1 ]: res += (ord (each)-64 )*(26 **(up-1 )) up += 1 return res
还可以这么写:
1 2 3 4 5 6 class Solution : def titleToNumber (self, s: str ) -> int : n = 0 for ch in s: n = n*26 + ord (ch)-65 +1 return n
经验:转为数值的时候,一般都是倒序输出,每位数乘以进制的N次方
给定一个整数 n ,返回 n ! 结果尾数中零的数量。
示例 1:
1 2 3 输入: 3 输出: 0 解释: 3! = 6, 尾数中没有零。
示例 2:
1 2 3 输入: 5 输出: 1 解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O (log n ) 。
有几个零靠的是个位数,根据九九乘法表,只有二五,四五,六五,八五才能得到一个整数.
我的代码:(是错的)
1 2 3 4 5 6 7 class Solution (object def trailingZeroes (self, n ): quo,remain = divmod (n,10 ) res = quo * 2 if remain >= 5 : res += 1 return res
上面的代码问题就在当n=25的时候,25可以拆除两个5,所以会多出一个0,同理50会多出2个0
所以我们需要计算到底有多少个5
假若N=31,31里能凑10的5为[5, 2*5, 3*5, 4*5, 25, 6*5] 其中 25还能拆为 5**2
所以,里面的5的个数为 int(31/(5**1)) + int(31/(5**2))
所以,只要先找个一个 5**x < n 的x的最大数 然后按上面循环加起来
结论就是:数n中含有5的幂次的个数之和就是答案,直观一点 answer = n//5+n//25 +n// 125 +n//625 + n//3125+.......
所以正确答案如下:
1 2 3 4 5 6 7 8 9 class Solution (object def trailingZeroes (self, n ): res = 0 while n != 0 : n //= 5 res += n return res
当前SQL架构如下:
1 2 3 4 5 6 Create table Person (PersonId int , FirstName varchar (255 ), LastName varchar (255 ))Create table Address (AddressId int , PersonId int , City varchar (255 ), State varchar (255 ))Truncate table Personinsert into Person (PersonId, LastName, FirstName) values ('1' , 'Wang' , 'Allen' )Truncate table Addressinsert into Address (AddressId, PersonId, City, State) values ('1' , '2' , 'New York City' , 'New York' )
表1: Person
1 2 3 4 5 6 7 8 +-------------+---------+ | 列名 | 类型 | +-------------+---------+ | PersonId | int | | FirstName | varchar | | LastName | varchar | +-------------+---------+ PersonId 是上表主键
表2: Address
1 2 3 4 5 6 7 8 9 +-------------+---------+ | 列名 | 类型 | +-------------+---------+ | AddressId | int | | PersonId | int | | City | varchar | | State | varchar | +-------------+---------+ AddressId 是上表主键
编写一个 SQL 查询,满足条件:无论 person 是否有地址信息,都需要基于上述两表提供 person 的以下信息:
1 FirstName, LastName, City, State
SQL中Truncate的用法:
1 2 3 truncate table命令用于删除现有表中完整的数据。(删除内容、释放空间但不删除定义。) 删除表中的数据的方法有delete,truncate, 其中TRUNCATE TABLE用于删除表中的所有行,而不记录单个行删除操作。TRUNCATE TABLE 与没有 WHERE 子句的 DELETE 语句类似;但是,TRUNCATE TABLE 速度更快,使用的系统资源和事务日志资源更少。 当你不再需要该表时,用 drop;当你仍要保留该表,但要删除所有记录时,用 truncate;当你要删除部分记录时(always with a WHERE clause), 用 delete.
其实考的就是left join 和 right join
代码如下:
1 2 3 SELECT p.FirstName, p.LastName, a.City, a.State FROM Person p LEFT JOIN Address a ON p.PersonId = a.personId;
left join 和 right join复习:返回左表的全部行 ,可能右表中没有匹配的行。
当前SQL架构如下:
1 2 3 4 5 Create table If Not Exists Employee (Id int , Salary int )Truncate table Employeeinsert into Employee (Id, Salary) values ('1' , '100' )insert into Employee (Id, Salary) values ('2' , '200' )insert into Employee (Id, Salary) values ('3' , '300' )
编写一个 SQL 查询,获取 Employee 表中第二高的薪水(Salary) 。
1 2 3 4 5 6 7 +----+--------+ | Id | Salary | +----+--------+ | 1 | 100 | | 2 | 200 | | 3 | 300 | +----+--------+
例如上述 Employee 表,SQL查询应该返回 200 作为第二高的薪水。如果不存在第二高的薪水,那么查询应返回 null。
1 2 3 4 5 +---------------------+ | SecondHighestSalary | +---------------------+ | 200 | +---------------------+
代码如下:
1 2 select max (salary) as SecondHighestSalary from employeewhere salary < (select max (salary) from employee);
或者:
1 2 3 select max (Salary) as SecondHighestSalary from Employee where Salary not in (select max (Salary) as Salary from Employee);
或者:
1 2 3 4 5 select IFNULL( (select Salary from Employee group by Salary order by Salary desc limit 1 ,1 ) ,null ) as SecondHighestSalary;
当前SQL架构如下:
1 2 3 4 5 6 Create table If Not Exists Employee (Id int , Name varchar (255 ), Salary int , ManagerId int )Truncate table Employeeinsert into Employee (Id, Name, Salary, ManagerId) values ('1' , 'Joe' , '70000' , '3' )insert into Employee (Id, Name, Salary, ManagerId) values ('2' , 'Henry' , '80000' , '4' )insert into Employee (Id, Name, Salary, ManagerId) values ('3' , 'Sam' , '60000' , 'None' )insert into Employee (Id, Name, Salary, ManagerId) values ('4' , 'Max' , '90000' , 'None' )
Employee 表包含所有员工,他们的经理也属于员工。每个员工都有一个 Id,此外还有一列对应员工的经理的 Id。
1 2 3 4 5 6 7 8 +----+-------+--------+-----------+ | Id | Name | Salary | ManagerId | +----+-------+--------+-----------+ | 1 | Joe | 70000 | 3 | | 2 | Henry | 80000 | 4 | | 3 | Sam | 60000 | NULL | | 4 | Max | 90000 | NULL | +----+-------+--------+-----------+
给定 Employee 表,编写一个 SQL 查询,该查询可以获取收入超过他们经理的员工的姓名。在上面的表格中,Joe 是唯一一个收入超过他的经理的员工。
1 2 3 4 5 +----------+ | Employee | +----------+ | Joe | +----------+
代码如下:
1 2 3 SELECT Name Employee FROM Employee AS aWHERE Salary > (SELECT Salary FROM Employee WHERE Id = a.Managerid);
或者:
1 2 SELECT e.Name AS Employee FROM Employee eINNER JOIN Employee y ON e.ManagerId = y.Id AND e.Salary > y.Salary;
当前SQL架构如下:
1 2 3 4 5 Create table If Not Exists Person (Id int , Email varchar (255 ))Truncate table Personinsert into Person (Id, Email) values ('1' , 'a@b.com' )insert into Person (Id, Email) values ('2' , 'c@d.com' )insert into Person (Id, Email) values ('3' , 'a@b.com' )
编写一个 SQL 查询,查找 Person 表中所有重复的电子邮箱。
示例:
1 2 3 4 5 6 7 +----+---------+ | Id | Email | +----+---------+ | 1 | a@b.com | | 2 | c@d.com | | 3 | a@b.com | +----+---------+
根据以上输入,你的查询应返回以下结果:
1 2 3 4 5 +---------+ | Email | +---------+ | a@b.com | +---------+
说明: 所有电子邮箱都是小写字母。
代码如下:
1 select Email from Person group by Email having count (Email) > 1 ;
或者:
1 SELECT p.email FROM Person p GROUP BY p.email HAVING COUNT (p.email) > 1 ;
当前SQL架构如下:
1 2 3 4 5 6 7 8 9 10 Create table If Not Exists Customers (Id int , Name varchar (255 ))Create table If Not Exists Orders (Id int , CustomerId int )Truncate table Customersinsert into Customers (Id, Name) values ('1' , 'Joe' )insert into Customers (Id, Name) values ('2' , 'Henry' )insert into Customers (Id, Name) values ('3' , 'Sam' )insert into Customers (Id, Name) values ('4' , 'Max' )Truncate table Ordersinsert into Orders (Id, CustomerId) values ('1' , '3' )insert into Orders (Id, CustomerId) values ('2' , '1' )
某网站包含两个表,Customers 表和 Orders 表。编写一个 SQL 查询,找出所有从不订购任何东西的客户。
Customers 表:
1 2 3 4 5 6 7 8 +----+-------+ | Id | Name | +----+-------+ | 1 | Joe | | 2 | Henry | | 3 | Sam | | 4 | Max | +----+-------+
Orders 表:
1 2 3 4 5 6 +----+------------+ | Id | CustomerId | +----+------------+ | 1 | 3 | | 2 | 1 | +----+------------+
例如给定上述表格,你的查询应返回:
1 2 3 4 5 6 +-----------+ | Customers | +-----------+ | Henry | | Max | +-----------+
代码:
1 2 select name as Customers from Customerswhere Id not in (select CustomerId from Orders)
或者:
1 2 3 SELECT c.Name AS Customers FROM Customers c LEFT JOIN Orders o ON c.Id = o.CustomerId WHERE o.CustomerId IS NULL ;
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
1 2 3 4 5 6 输入: [1,2,3,4,5,6,7] 和 k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右旋转 1 步: [7,1,2,3,4,5,6] 向右旋转 2 步: [6,7,1,2,3,4,5] 向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
1 2 3 4 5 输入: [-1,-100,3,99] 和 k = 2 输出: [3,99,-1,-100] 解释: 向右旋转 1 步: [99,-1,-100,3] 向右旋转 2 步: [3,99,-1,-100]
说明:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
要求使用空间复杂度为 O(1) 的原地算法。
最简单的代码,但是空间复杂度为O(k),而且不是原地算法:
1 2 3 class Solution (object def rotate (self, nums, k ): return nums[-k:] + nums[:-k]
或者:
1 2 3 4 class Solution (object def rotate (self, nums, k ): for _ in range (k): nums.insert(0 ,nums.pop())
还有如下代码:
1 2 3 4 5 6 7 8 9 10 11 class Solution (object def rotate (self, nums, k ): n = len (nums) k %= n if k == 0 : return tmp = nums[:] for i in range (n): nums[(i+k)%n] = tmp[i]
还有很酷的方法:三次反转
1 2 3 4 5 6 7 8 9 10 11 class Solution (object def rotate (self, nums, k ): n = len (nums) k %= n if n == 0 or k == 0 : return nums[:n-k] = reversed (nums[:n-k]) nums[n-k:] = reversed (nums[n-k:]) nums.reverse()
也可以写成如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution (object def rotate (self, nums, k ): n = len (nums) k %= n self.func(nums, 0 , n-1 ) self.func(nums, 0 , k-1 ) self.func(nums, k, n-1 ) def func (self, nums, start, end ): while start < end: nums[start],nums[end]=nums[end],nums[start] start += 1 end -= 1
最pythonic的代码:
1 2 3 4 5 6 7 8 9 class Solution (object def rotate (self, nums, k ): n = len (nums) k %= n if k == 0 : return nums[:] = nums[n-k:]+nums[0 :n-k]
经验:
如果是非原地修改就是return nums[n-k:]+nums[0:n-k],
对于旋转数组问题,可以考虑三次翻转.
颠倒给定的 32 位无符号整数的二进制位。
示例 1:
1 2 3 输入: 00000010100101000001111010011100 输出: 00111001011110000010100101000000 解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,因此返回 964176192,其二进制表示形式为00111001011110000010100101000000。
示例 2:
1 2 3 输入:11111111111111111111111111111101 输出:10111111111111111111111111111111 解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,因此返回 3221225471 其二进制表示形式为 10101111110010110010011101101001。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码 记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
进阶 :
代码如下:
1 2 3 4 5 6 7 8 class Solution : def reverseBits (self, n ): str1 = bin (n)[2 :][::-1 ] while len (str1)<32 : str1 += '0' return int (str1,2 )
上面代码效率不高,应该使用右移
1 2 3 4 5 6 7 8 9 10 class Solution : def reverseBits (self, n ): rev = 0 for i in range (32 ): pop = n & 1 n >>= 1 rev = rev*2 + pop return rev
python位运算符复习:x** 类似于 -x-1 | (a ) 输出结果 -61 ,二进制解释: 1100 0011,在一个有符号二进制数的补码形式。|<<** 右边的数字指定了移动的位数,高位丢弃,低位补0。| a << 2 输出结果 240 ,二进制解释: 1111 0000 | >>** 右边的数字指定了移动的位数 | a >> 2 输出结果 15 ,二进制解释: 0000 1111 |
示例:
1 2 3 4 5 6 7 8 9 a = 60 b = 13 c = a & b; c = a | b; c = a ^ b; c = ~a; c = a << 2 ; c = a >> 2 ;
编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量 )。
示例 1:
1 2 3 输入:00000000000000000000000000001011 输出:3 解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
1 2 3 输入:00000000000000000000000010000000 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
1 2 3 输入:11111111111111111111111111111101 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码 记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
进阶 :
可以耍赖使用字符串的count函数:
1 2 3 class Solution (object def hammingWeight (self, n ): return bin (n).count('1' )
经验:==不仅str类型有count函数,byte类型一样有count函数==
最正确的方式还是使用位运算:
1 2 3 4 5 6 7 8 class Solution (object def hammingWeight (self, n ): count = 0 while n: n &= (n-1 ) count += 1 return count