有序二维数组的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
矩阵是有序的,从左下角来看,向上数字递减,向右数字递增,因此从左下角开始查找,
当要查找数字比左下角数字大时。右移
要查找数字比左下角数字小时,上移
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution : def Find (self, target, array ): x = 0 y = len (array) - 1 while x <= len (array[0 ]) - 1 and y >= 0 : if array[x][y] < target: x += 1 elif array[x][y] > target: y -= 1 else : return True return False s = Solution() print (s.Find(7 ,[[1 ,2 ,8 ,9 ],[2 ,4 ,9 ,12 ],[4 ,7 ,10 ,13 ],[6 ,8 ,11 ,15 ]]))
使用递归的倒序属性 输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
1 2 3 4 5 6 class Solution : def printListFromTailToHead (self, listNode ): if not listNode: return [] else : return self.printListFromTailToHead(listNode.next ) + [listNode.val]
重建二叉树 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
先求出根节点(前序序列第一个元素)。
将根节点带入到中序遍历序列中求出左右子树的中序遍历序列。
通过左右子树的中序序列元素集合带入前序遍历序列可以求出左右子树的前序序列。
左右子树的前序序列第一个元素分别是根节点的左右儿子
求出了左右子树的4种序列可以递归上述步骤
1 2 3 4 5 6 7 8 9 10 class Solution : def reConstructBinaryTree (self, pre, tin ): if not pre or not tin: return None root = TreeNode(pre.pop(0 )) index = tin.index(root.val) root.left = self.reConstructBinaryTree(pre, tin[:index]) root.right = self.reConstructBinaryTree(pre, tin[index + 1 :]) return root
旋转数组的最小数字 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
最大的陷阱:
{1,0,1,1,1} 和 {1,1, 1,0,1}都可以看成是递增排序数组{0,1,1,1,1}的旋转。
这种情况下我们无法继续用上一道题目的解法,去解决这道题目。因为在这两个数组中,第一个数字,最后一个数字,中间数字都是1。
只能使用遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def minNumberInRotateArray (self, rotateArray ): if not rotateArray: return front = 0 rear = len (rotateArray)-1 if rotateArray[front] < rotateArray[rear]: return rotateArray[front] mid = (front + rear) // 2 if rotateArray[front] == rotateArray[mid] and rotateArray[rear] == rotateArray[mid]: return self.Inorder(rotateArray) while front + 1 < rear: if rotateArray[mid] >= rotateArray[front]: front = mid else : rear = mid mid = (front + rear) // 2 return rotateArray[rear] def Inorder (self, rotateArray ): result = rotateArray[0 ] for i in range (1 , len (rotateArray)): if rotateArray[i] < result: result = rotateArray[i] return result
青蛙跳台阶 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
关于本题,前提是n个台阶会有一次n阶的跳法。分析如下:
f(1) = 1
f(2) = f(2-1) + f(2-2) //f(2-2) 表示2阶一次跳2阶的次数。
f(3) = f(3-1) + f(3-2) + f(3-3)
…
f(n) = f(n-1) + f(n-2) + f(n-3) + … + f(n-(n-1)) + f(n-n)
这里的f(n) 代表的是n个台阶有一次1,2,…n阶的 跳法数。
n = 1时,只有1种跳法,f(1) = 1
n = 2时,会有两个跳得方式,一次1阶或者2阶,这回归到了问题(1) ,f(2) = f(2-1) + f(2-2)
n = 3时,会有三种跳得方式,1阶、2阶、3阶,
那么就是第一次跳出1阶后面剩下:f(3-1);第一次跳出2阶,剩下f(3-2);第一次3阶,那么剩下f(3-3)
因此结论是f(3) = f(3-1)+f(3-2)+f(3-3)
n = n时,会有n中跳的方式,1阶、2阶…n阶,得出结论:
f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n) => f(0) + f(1) + f(2) + f(3) + … + f(n-1)
由以上已经是一种结论,但是为了简单,我们可以继续简化:
f(n-1) = f(0) + f(1)+f(2)+f(3) + … + f((n-1)-1) = f(0) + f(1) + f(2) + f(3) + … + f(n-2)
f(n) = f(0) + f(1) + f(2) + f(3) + … + f(n-2) + f(n-1) = f(n-1) + f(n-1)
可以得出:
f(n) = 2*f(n-1)
得出最终结论,在n阶台阶,一次有1、2、…n阶的跳的方式时,总得跳法为:
| 1 ,(n=0 )
f(n) = | 1 ,(n=1 )
| 2*f(n-1),(n>=2)
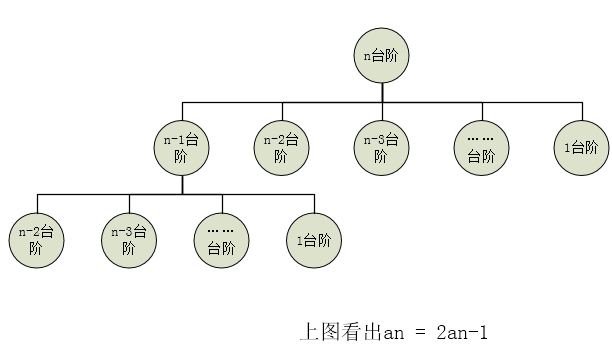
若有n个台阶,则 跳法为第一下跳1阶剩余台阶的 跳法为f(n-1),以及第一下跳2节剩余台阶跳法为f(n-2),以及第一下跳3阶剩余台阶 跳法为f(n-3),依次类推知道最后一次是一下子全部跳上去,方法为1,
因此f(n)=f(n-1)+f(n-2)+f(n-3)+…+f(1)+1,f(1)=1,f(2)=2..f(n)-f(n-1)=f(n-1)因此f(n)=2f(n-1)是等比数列,首项为1,比例 为2,f(n)=2^(n-1)
1 2 3 class Solution : def jumpFloorII (self, number ): return 2 **(number-1 )
列表排序 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的索引为奇数的元素位于数组的前半部分,所有的索引为偶数的元素位于数组的后半部分,排序算法稳定。
1 2 3 class Solution : def reOrderArray (self, array ): return sorted (array,key= lambda ele : array.index(ele) % 2 == 1 )
最大的坑:
1 2 3 4 class Solution : def reOrderArray (self, array ): return array.sort(key=lambda ele : array.index(ele) % 2 == 1 )
原因 : array.sort是原地操作 , sorted是复制后操作
链表中倒数第k个结点
双指针法 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def FindKthToTail (self, head, k ): if head==None or k<=0 : return None p1=p2=head while k>1 : if p2.next : p2=p2.next k-=1 else : return None while p2.next : p1=p1.next p2=p2.next return p1
树的子结构 输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是 任意一个树的子结构)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def HasSubtree (self, pRoot1, pRoot2 ): return False if not pRoot2 else self.core(pRoot1,pRoot2) def core (self, pRoot1, pRoot2 ): if not pRoot2: return True if not pRoot1: return False else : if pRoot1.val == pRoot2.val and self.core(pRoot1.left,pRoot2.left) and self.core(pRoot1.right,pRoot2.right): return True return self.core(pRoot1.left,pRoot2) or self.core(pRoot1.right,pRoot2)
骚操作:
1 2 3 4 5 6 7 8 9 class Solution : def HasSubtree (self, pRoot1, pRoot2 ): def convert (p ): if p: return str (p.val) + convert(p.left) + convert(p.right) else : return "" return convert(pRoot2) in convert(pRoot1) if pRoot2 else False
顺时针打印矩阵 输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵:
1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
我的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution : def printMatrix (self, matrix ): startRow = [0 ,0 ] endRow = [len (matrix)-1 ,0 ] startCol = [0 ,len (matrix[0 ])-1 ] endCol = [len (matrix)-1 ,len (matrix[0 ]) - 1 ] res = [] while startRow[0 ] < endCol[0 ] and startRow[1 ] < endCol[1 ]: for idx in range (startRow[1 ],startCol[1 ]+1 ): res.append(matrix[startRow[0 ]][idx]) for idx in range (startCol[0 ]+1 ,endCol[0 ]+1 ): res.append(matrix[idx][startCol[1 ]]) for idx in range (endCol[1 ]-1 ,endRow[1 ]-1 ,-1 ): res.append(matrix[endRow[0 ]][idx]) for idx in range (endRow[0 ]-1 ,startRow[0 ],-1 ): res.append(matrix[idx][startRow[0 ]]) startRow[0 ] += 1 startRow[1 ] += 1 endRow[0 ] -= 1 endRow[1 ] += 1 startCol[0 ] += 1 startCol[1 ] -= 1 endCol[0 ] -= 1 endCol[1 ] -= 1 return res s = Solution() matrix = [ [1 ,2 ,3 ,4 ], [5 ,6 ,7 ,8 ], [9 ,10 ,11 ,12 ], [13 ,14 ,15 ,16 ], ] print (s.printMatrix(matrix))
正确思路 :
打印一圈
从左到右打印一行(这是一定有的)
当有两行及以上时,存在从上到下打印
当有两行及以上并有两列及以上时,存在从右到左
当有两列并有三行及以上时,存在从下到上打打印
起点进入下一圈,即进入下一个循环
初始几点为(0, 0), 打印一圈后有(1, 1), 再打印一圈为(2, 2)
都存在行数 > 起点 * 2 并且列数 > 起点 * 2
简单来说就是, 如果把二维数组等分为四个部分 中点都为中心,那么起点肯定都位于左上部分。根据这个条件可以判断是否还有圈数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution : def printMatrix (self, matrix ): if not matrix: return [] columns = len (matrix[0 ]) rows = len (matrix) def printMatrixCircle (start ): endRow = rows - 1 - start endColumn = columns - 1 - start for y in range (start, endColumn + 1 ): result.append(matrix[start][y]) if endRow > start: for x in range (start + 1 , endRow + 1 ): result.append(matrix[x][endColumn]) if endColumn > start and endRow > start: for y in range (endColumn - 1 , start - 1 , -1 ): result.append(matrix[endRow][y]) if endRow > start + 1 and endColumn > start: for x in range (endRow - 1 , start, -1 ): result.append(matrix[x][start]) start = 0 result = [] while columns > start * 2 and rows > start * 2 : printMatrixCircle(start) start += 1 return result
也可以使用如下思路:
用旋转魔法的方式,一直取出第一行;
例如
1 2 3
4 5 6
7 8 9
输出并删除第一行后,变为
4 5 6
7 8 9
再进行一次逆时针旋转,就变成:
6 9
5 8
4 7
继续重复上述操作即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def printMatrix (self, matrix ): res = [] while matrix: res.extend(matrix[0 ]) matrix = list (zip (*matrix[1 :]))[::-1 ] return res matrix = [ [1 ,2 ,3 ,4 ], [5 ,6 ,7 ,8 ], [9 ,10 ,11 ,12 ], [13 ,14 ,15 ,16 ], ] s = Solution() print (s.printMatrix(matrix))
由此我们得出反转矩阵的代码:
1 matrix = list (zip (*matrix[1 :]))[::-1 ]
包含min函数的栈 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
思路:利用一个辅助栈来存放最小值
栈 3,4,2,5,1
辅助栈 3,3,2,2,1
每入栈一次,就与辅助栈顶比较大小,如果小就入栈,如果大就入栈当前的辅助栈顶
当出栈时,辅助栈也要出栈
这种做法可以保证辅助栈顶一定都当前栈的最小值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution : def __init__ (self ): self.stack = [] self.assist = [] def push (self, node ): min = self.min () if not min or node < min : self.assist.append(node) else : self.assist.append(min ) self.stack.append(node) def pop (self ): if self.stack: self.assist.pop() return self.stack.pop() def top (self ): if self.stack: return self.stack[-1 ] def min (self ): if self.assist: return self.assist[-1 ]
栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。
例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
模拟这个过程 :
借用一个辅助的栈,遍历压栈顺序,先讲第一个放入栈中,这里是1,然后判断栈顶元素是不是出栈顺序的第一个元素,这里是4,很显然1≠4,所以我们继续压栈,直到相等以后开始出栈,出栈一个元素,则将出栈顺序向后移动一位,直到不相等,这样循环等压栈顺序遍历完成,如果辅助栈还不为空,说明弹出序列不是该栈的弹出顺序。
举例:
入栈1,2,3,4,5
出栈4,5,3,2,1
首先1入辅助栈,此时栈顶1≠4,继续入栈2
此时栈顶2≠4,继续入栈3
此时栈顶3≠4,继续入栈4
此时栈顶4=4,出栈4,弹出序列向后一位,此时为5,,辅助栈里面是1,2,3
此时栈顶3≠5,继续入栈5
此时栈顶5=5,出栈5,弹出序列向后一位,此时为3,,辅助栈里面是1,2,3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def IsPopOrder (self, pushV, popV ): stack = [] while popV: if stack and stack[-1 ]==popV[0 ]: stack.pop() popV.pop(0 ) elif pushV: stack.append(pushV.pop(0 )) else : return False return True s = Solution() print (s.IsPopOrder([1 ,2 ,3 ,4 ,5 ],[4 ,5 ,3 ,2 ,1 ]))
从上往下打印二叉树 从上往下打印出二叉树的每个节点,同层节点从左至右打印。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def PrintFromTopToBottom (self, root ): if not root: return [] print_li = [] floor_li = [root] while floor_li: temp = [] for node in floor_li: print_li.append(node.val) if node.left: temp.append(node.left) if node.right: temp.append(node.right) floor_li = temp return print_li
二叉搜索树的后序遍历序列 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
知道二叉搜索树的后序遍历,那么就知道二叉搜索树的中序遍历
BST的后序序列的合法序列是:
后序遍历的序列中,最后一个数字是树的根节点 ,数组中前面的数字可以分为两部分:
第一部分是左子树节点 的值,都比根节点的值小 ;
第二部分是右子树 节点的值,都比根节点的值大 ,后面用递归分别判断前后两部分 是否 符合以上原则
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def VerifySquenceOfBST (self, sequence ): if not sequence: return False length = len (sequence) root = sequence[length-1 ] for i in range (length): if sequence[i]>root: break for j in range (i,length): if sequence[j]<root: return False left = True if i > 0 : left = self.VerifySquenceOfBST(sequence[0 :i]) right = True if i < length-1 : right = self.VerifySquenceOfBST(sequence[i:-1 ]) return left and right
二叉树中和为某一值的路径 输入一颗二叉树的根节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def FindPath (self, root, expectNumber ): def subFindPath (root ): if root: b.append(root.val) if not root.right and not root.left and sum (b) == expectNumber: a.append(b[:]) else : subFindPath(root.left),subFindPath(root.right) b.pop() a, b = [], [] subFindPath(root) return a
得出一个经验:
对于一个递归函数来说,如果要引入二维表的话,可以考虑定义来个列表
然后一个list去append另一个list
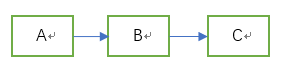
复杂链表的复制 输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的head。
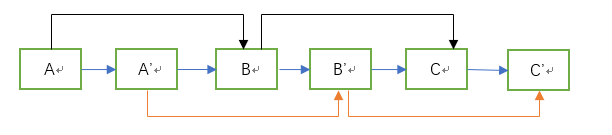
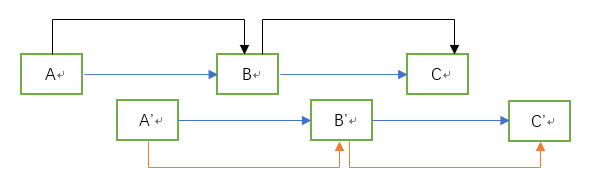
遍历链表,复制链表中的每个结点,并将复制的结点插入到该结点的后面。例如,原链表为A->B->C, 遍历完毕后,链表变为A->A’->B->B’->C->C’,其中A‘,B’,C’是结点A,B,C的复制结点。看图中,蓝色箭头为next指针:
复制结点后:
为复制结点的random指针赋值
如果原结点的random指针指向的是结点B,那么将复制结点的random指针指向结点B的复制结点B’。
图中黑色箭头为random指针:复制结点的random指针赋值后:
将链表的原始结点与复制结点分割至两个链表,使原始结点构成一个链表,复制结点构成一个链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution : def Clone (self, pHead ): pNode = pHead if pHead == None : return None self.connectnodes(pHead) self.connectrandomnodes(pHead) return self.reconnectnodes(pHead) def connectnodes (self,pHead ): pNode = pHead while (pNode): pClone = RandomListNode(0 ) pClone.label = pNode.label pClone.next = pNode.next pClone.random = None pNode.next = pClone pNode = pClone.next def connectrandomnodes (self,pHead ): pNode = pHead while (pNode): pClone = pNode.next if pNode.random: pClone.random = pNode.random.next pNode = pClone.next def reconnectnodes (self,pHead ): pNode = pHead pHeadclone = pClone = pNode.next pNode.next = pClone.next pNode = pClone.next while pNode: pClone.next = pNode.next pClone = pClone.next pNode.next = pClone.next pNode = pNode.next return pHeadclone
二叉搜索树与双向链表 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def Convert (self, pRootOfTree ): def get_tree (pRootOfTree ): if pRootOfTree.left: get_tree(pRootOfTree.left) node_list.append(pRootOfTree) if pRootOfTree.right: get_tree(pRootOfTree.right) if not pRootOfTree: return None node_list = [] get_tree(pRootOfTree) head = node_list[0 ] for node1,node2 in zip (node_list,node_list[1 :]): node1.right = node2 node2.left = node1 return head
也可以:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def Convert (self, pRootOfTree ): if not pRootOfTree: return None p = pRootOfTree stack = [] resStack = [] while p or stack: if p: stack.append(p) p = p.left else : node = stack.pop() resStack.append(node) p = node.right resP = resStack[0 ] while resStack: top = resStack.pop(0 ) if resStack: top.right = resStack[0 ] resStack[0 ].left = top return resP
至此,我们得出了不用递归的中序遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 p = pRootOfTree stack = [] resStack = [] while p or stack: if p: stack.append(p) p = p.left else : node = stack.pop() resStack.append(node) p = node.right
字符串的排列
输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。按字典序打印出该字符串中字符的所有排列。
例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def Permutation (self, ss ): if len (ss)==0 : return [] if len (ss)==1 : return [ss] res=set () for i in range (len (ss)): for j in self.Permutation(ss[:i]+ss[i+1 :]): res.add(ss[i]+j) return sorted (list (res)) s = Solution() print (s.Permutation('abc' ))
数组中出现次数超过一半的数字 数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def MoreThanHalfNum_Solution (self, numbers ): count = 1 cur = numbers[0 ] for num in numbers[1 :]: if cur == num: count += 1 else : count -= 1 if count == 0 : cur = num count = 1 c = 0 for num in numbers: if num == cur: c += 1 if 2 *c > len (numbers): return cur else : return 0
连续子数组的最大和
计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?
例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
dp[i] = max{ dp[i-1]+array[i] , array[i] }.
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def FindGreatestSumOfSubArray (self, array ): opt = [float ('-inf' )] * len (array) opt[0 ] = array[0 ] for idx in range (1 ,len (array)): planA = opt[idx-1 ] + array[idx] planB = array[idx] opt[idx] = max (planA,planB) return max (opt) print (Solution().FindGreatestSumOfSubArray([6 ,-3 ,-2 ,7 ,-15 ,1 ,2 ,2 ]))
整数中1出现的次数(从1到n整数中1出现的次数) 计算从1 到 n 中1出现的次数
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def NumberOf1Between1AndN_Solution (self,n ): count = 0 for num in range (1 ,n+1 ): while num != 0 : num,remain = divmod (num,10 ) if remain == 1 : count += 1 return count s = Solution() print (s.NumberOf1Between1AndN_Solution(1 ))
把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
模仿快排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def PrintMinNumber (self, numbers ): numbers = list (map (str ,numbers)) res = self.core(numbers) return '' .join(res) def core (self, numbers ): if len (numbers) <= 1 : return numbers else : val = numbers[0 ] left = self.core([num for num in numbers[1 :] if val + num >= num + val]) right = self.core([num for num in numbers[1 :] if val + num < num + val]) return left + [val] + right s = Solution() print (s.PrintMinNumber([3 ,32 ,321 ]))print (s.PrintMinNumber([1 ,11 ,111 ]))
丑数 把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def GetUglyNumber_Solution (self, index ): if not index: return 0 res = [0 ,1 ] i2 = i3 = i5 = 1 while (index-1 ): x,y,z = res[i2]*2 ,res[i3]*3 ,res[i5]*5 if x <= y and x <= z: tar = x i2 += 1 elif y <= x and y <= z: tar = y i3 += 1 else : tar = z i5 += 1 if tar != res[-1 ]: res.append(tar) index -= 1 return res[-1 ]
数组中的逆序对 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
题目保证输入的数组中没有的相同的数字
数据范围:
对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
输入1,2,3,4,5,6,7,0 , 输出7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 count = 0 class Solution : def InversePairs (self, data ): global count def MergeSort (lists ): global count if len (lists) <= 1 : return lists num = len (lists) // 2 left = MergeSort(lists[:num]) right = MergeSort(lists[num:]) r, l=0 , 0 result=[] while l<len (left) and r<len (right): if left[l] < right[r]: result.append(left[l]) l += 1 else : result.append(right[r]) r += 1 count += len (left)-l result += right[r:] result += left[l:] return result MergeSort(data) return count%1000000007
数组中只出现一次的数字 一个整型数组里除了两个数字 之外,其他的数字都出现了两次 。请写程序找出这两个只出现一次的数字。
异或的性质:两个相同数字异或=0,一个数和0异或还是它本身。
看两个数(我们假设是AB),先异或,剩下的数字肯定是A、B异或的结果,这个结果的二进制中的1,表现的是A和B的不同的位 。我们就取第一个1所在的位数,假设是第3位,接着把原数组分成两组 ,分组标准是第3位是否为1。如此,相同的数肯定在一个组 ,因为相同数字所有位都相同,而不同的数,肯定不在一组 。然后把这两个组按照最开始的思路,依次异或,剩余的两个结果就是这两个只出现一次的数字。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def FindNumsAppearOnce (self, array ): if not array: return [] tmp = 0 for i in array: tmp ^= i idx = 0 while (tmp & 1 ) == 0 : tmp >>= 1 idx += 1 a = b = 0 for i in array: if self.isBit(i, idx): a ^= i else : b ^= i return [a, b] def isBit (self, num, idx ): """ 判断num的二进制从低到高idx位是不是1 :param num: 数字 :param idx: 二进制从低到高位置 :return: num的idx位是否为1 """ num = num >> idx return num & 1
和为S的连续正数序列
计算出9~16的和,马上就写出了正确答案是100。
有多少种连续的正数序列的和为100(至少包括两个数)。
找出所有和为S的连续正数序列?
输出所有和为S的连续正数序列。序列内按照从小至大的顺序,序列间按照开始数字从小到大的顺序
双指针 , left=1,right=2
如果当前窗口内的值之和小于sum,那么右边窗口右移一下 , 如果当前窗口内的值之和大于sum,那么左边窗口右移一下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def FindContinuousSequence (self, tsum ): left = 1 right = 2 res = [] while left < right: tmp = (left + right) * ((right - left + 1 ) / 2 ) if tmp > tsum: left += 1 elif tmp < tsum: right += 1 else : res.append([num for num in range (left,right+1 )]) right += 1 left += 1 return res s = Solution() print (s.FindContinuousSequence(100 ))
一般双指针都是左右不断缩小的,
要注意这种双指针不断扩大的类型
扑克牌顺子
普通扑克牌 , 多加大小王各一张 .
王能视任何牌 .A看作1,J为11,Q为12,K为13
现在给5张牌 , 看是否能组成顺子(为了方便起见,大小王表示为0。)
排序,计算前面0的个数zeros
然后zeros - (顺子差的数)
若zeros最后 >= 0 说明用大小王补够用 否则不行
还要判断一下只要有相同的牌直接返回false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def IsContinuous (self, numbers ): if not numbers: return False numbers.sort() zero_count = 0 for pocker in numbers: if pocker == 0 : zero_count += 1 else : break numbers = numbers[zero_count:] if len (numbers) != len (set (numbers)): return False else : for num in range (numbers[0 ]+1 ,numbers[-1 ]+1 ): if num not in numbers: zero_count -= 1 if zero_count < 0 : return False return True s = Solution() print (s.IsContinuous([1 ,3 ,0 ,5 ,0 ]))
求1+2+3+…+n 求1+2+3+…+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
1 2 3 4 5 6 class Solution : def Sum_Solution (self, n ): res = n temp = res and self.Sum_Solution(n-1 ) res += temp return res
甚至:
1 2 3 class Solution : def Sum_Solution (self, n ): return n and n + self.Sum_Solution(n-1 )
不用加减乘除做加法 写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
1 2 3 4 5 class Solution : def Add (self, a, b ): while (b): a,b = (a^b) & 0xFFFFFFFF ,((a&b)<<1 ) & 0xFFFFFFFF return a if a<=0x7FFFFFFF else ~(a^0xFFFFFFFF )
把字符串转换成整数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def StrToInt (self, s ): if not s: return 0 sign = 1 if s[0 ] == '+' : s = s[1 :] elif s[0 ] == '-' : sign = -1 s = s[1 :] if not s: return 0 res = 0 mapping = ['1' ,'2' ,'3' ,'4' ,'5' ,'6' ,'7' ,'8' ,'9' ] for char in s: if char in mapping: res = mapping.index(char) + 1 + res * 10 else : return 0 return res * sign s = Solution() print (s.StrToInt('+' ))
数组中重复的数字 在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def duplicate (self, numbers, duplication ): cur = 0 while cur < len (numbers): if numbers[cur] == cur: cur += 1 continue if numbers[cur] == numbers[numbers[cur]]: duplication[0 ] = numbers[cur] return True temp = numbers[cur] numbers[cur] = numbers[numbers[cur]] numbers[temp] = temp return False
构建乘积数组
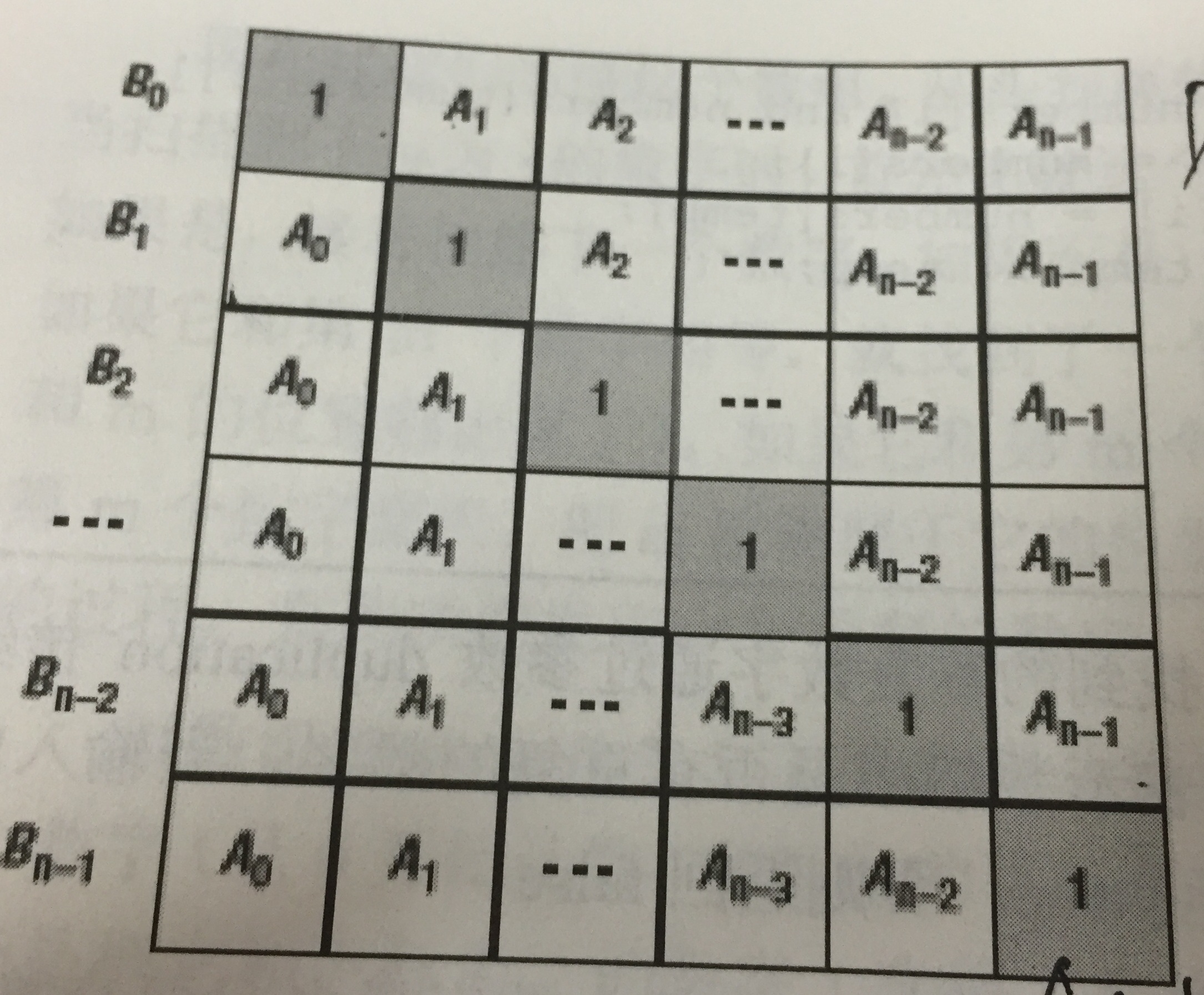
给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]*A[1]*…*A[i-1]*A[i+1]*…*A[n-1]。不能使用除法。
题目要求B的i个元素等于A中除了i个元素所有元素乘积
B[i]的值可以看作下图的矩阵中每行的乘积。 下三角用连乘可以很容求得,上三角,从下向上也是连乘。
因此我们的思路就很清晰了,先算下三角中的连乘,即我们先算出B[i]中的一部分,然后倒过来按上三角中的分布规律,把另一部分也乘进去。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution : def multiply (self, A ): res = [0 ] * len (A) res[0 ] = 1 for idx in range (1 ,len (A)): res[idx] = res[idx-1 ] * A[idx-1 ] tmp = 1 for idx in range (len (A)-2 ,-1 ,-1 ): tmp *= A[idx+1 ] res[idx] *= tmp return res s = Solution() print (s.multiply([1 ,2 ,3 ,4 ,5 ]))
正则表达式匹配 1 实现一个函数用来匹配包括'.'和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(包含0次)。 在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但是与"aa.a"和"ab*a"均不匹配
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution : def match (self, s, pattern ): if len (s) == 0 and len (pattern) == 0 : return True elif len (s) != 0 and len (pattern) == 0 : return False elif len (s) == 0 and len (pattern) != 0 : if len (pattern) > 1 and pattern[1 ] == '*' : return self.match(s, pattern[2 :]) else : return False else : if len (pattern) > 1 and pattern[1 ] == '*' : if s[0 ] != pattern[0 ] and pattern[0 ] != '.' : return self.match(s, pattern[2 :]) else : return self.match(s, pattern[2 :]) or self.match(s[1 :], pattern[2 :]) or self.match(s[1 :], pattern) else : if s[0 ] == pattern[0 ] or pattern[0 ] == '.' : return self.match(s[1 :], pattern[1 :]) else : return False
表示数值的字符串 实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串+100,5e2,-123,3.1416和-1E-16都表示数值。 但是12e,1a3.14,1.2.3,+-5和12e+4.3都不是。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution : def isNumeric (self, s ): if not s : return False has_point = False has_e = False for i in range (len (s)): if s[i]=='E' or s[i] =='e' : if has_e: return False else : has_e = True if i == len (s)-1 : return False elif s[i] =='+' or s[i] =='-' : if i != 0 and (s[i-1 ] != 'e' and s[i-1 ] != 'E' ): return False if i == len (s)-1 : return False elif s[i] =='.' : if has_point or has_e: return False else : has_point = True if i == len (s)-1 : return False else : if s[i] not in '0123456789' : return False return True
字符流中第一个不重复的字符 请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符”go”时,第一个只出现一次的字符是”g”。当从该字符流中读出前六个字符“google”时,第一个只出现一次的字符是”l”。如果当前字符流没有存在出现一次的字符,返回#字符。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution : def __init__ (self ): self.char_list = [-1 for i in range (256 )] self.index = 0 ''' 解法:利用一个int型数组表示256个字符,这个数组初值置为-1. 每读出一个字符,将该字符的位置存入字符对应数组下标中。 若值为-1标识第一次读入,不为-1且>0表示不是第一次读入,将值改为-2. 之后在数组中找到>0的最小值,该数组下标对应的字符为所求。 在python中,ord(char)是得到char对应的ASCII码;chr(idx)是得到ASCII位idx的字符 ''' def FirstAppearingOnce (self ): min_value = 500 min_idx = -1 for i in range (256 ): if self.char_list[i] > -1 : if self.char_list[i] < min_value: min_value = self.char_list[i] min_idx = i if min_idx > -1 : return chr (min_idx) else : return '#' def Insert (self, char ): if self.char_list[ord (char)] == -1 : self.char_list[ord (char)] = self.index elif self.char_list[ord (char)] == -2 : pass else : self.char_list[ord (char)] = -2 self.index += 1
链表中环的入口结点 给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def EntryNodeOfLoop (self, pHead ): l = [] while pHead: if id (pHead) not in l: l.append(id (pHead)) else : return pHead pHead = pHead.next return None
找环中相汇点。分别用p1,p2指向链表头部,p1每次走一步,p2每次走二步,直到p1==p2找到在环中的相汇点。
找环的入口。接上步,当p1=p2时,p2所经过节点数为2x,p1所经过节点数为x,设环中有n个节点,p2比p1多走一圈有2x=n+x; n=x;可以看出p1实际走了一个环的步数 ,
再让p2指向链表头部,p1位置不变,p1,p2每次走一步直到p1=p2; 此时p1指向环的入口。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def EntryNodeOfLoop (self, pHead ): low = fast = pHead while low and fast.next : low = low.next fast = fast.next .next if low == fast: low = pHead while low != fast: low = low.next fast = fast.next return low return None
删除链表中重复的结点 在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表1->2->3->3->4->4->5 处理后为 1->2->5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def deleteDuplication (self, pHead ): if not pHead or not pHead.next : return pHead else : dummy = pre = ListNode(None ) dummy.next = pHead while pHead and pHead.next : if pHead.val == pHead.next .val: while pHead.next and pHead.val == pHead.next .val: pHead.next = pHead.next .next pre.next = pHead.next pHead = pHead.next else : pre = pHead pHead = pHead.next return dummy.next
二叉树的下一个结点
给定一个二叉树其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。
注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def GetNext (self, pNode ): if pNode.right: p = pNode.right while p.left: p = p.left return p else : while pNode.next : if pNode.next .left == pNode: return pNode.next pNode = pNode.next return None
对于中序遍历问题 , 我们需要分成有右子树和没有右子树两个问题.
按之字形顺序打印二叉树 请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def Print (self, pRoot ): if not pRoot: return [] res = [] q = [pRoot] left2right = True while q: if left2right: l = [node.val for node in q] else : l = list (reversed ([node.val for node in q])) res.append(l) left2right = not left2right tmp = [] for node in q: if node.left: tmp.append(node.left) if node.right: tmp.append(node.right) q = tmp return res
序列化二叉树 请实现两个函数,分别用来序列化和反序列化二叉树
二叉树的序列化是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串,从而使得内存中建立起来的二叉树可以持久保存。
序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改,序列化的结果是一个字符串,序列化时通过某种符号表示空节点(#),以 ! 表示一个结点值的结束(value!)。
二叉树的反序列化是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution : def __init__ (self ): self.flag = -1 def Serialize (self, root ): if not root: return '#!' return str (root.val) + '!' + self.Serialize(root.left) + self.Serialize(root.right) def Deserialize (self, s ): self.flag += 1 l = s.split('!' ) if self.flag >= len (s): return None root = None if l[self.flag] != '#' : root = TreeNode(int (l[self.flag])) root.left = self.Deserialize(s) root.right = self.Deserialize(s) return root
或者:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def Serialize (self, root ): self.s = '' self.sarializeCore(root) return self.s def sarializeCore (self,root ): if root is None : self.s += "#," return self.s += str (root.val)+"," self.sarializeCore(root.left) self.sarializeCore(root.right) def Deserialize (self, s ): if s is None : return None if len (s)==1 and s[0 ]=="#" : return None self.index = 0 s= s.split(',' ) root = self.DeserializeCore(s) return root def DeserializeCore (self,s ): t = s[self.index] if t.isdigit(): root = TreeNode(int (t)) self.index +=1 left = self.DeserializeCore(s) right = self.DeserializeCore(s) root.left = left root.right = right return root elif t =="#" : self.index+=1 return None t = TreeNode(8 ) t1 =TreeNode(6 ) t2 = TreeNode(10 ) t3 = TreeNode(5 ) t4 =TreeNode(7 ) t5 = TreeNode(9 ) t6 = TreeNode(11 ) t.left = t1 t.right = t2 t1.left = t3 t1.right = t4 t2.left = t5 t2.right = t6 print Solution().Serialize(t)print Solution().Deserialize(Solution().Serialize(t))
数据流中的中位数 求一个数据流中的中位数?
我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 from heapq import *class Solution : def __init__ (self ): self.heaps = [], [] def Insert (self, num ): small, large = self.heaps heappush(small, -heappushpop(large, num)) if len (large) < len (small): heappush(large, -heappop(small)) def GetMedian (self,ss ): small,large = self.heaps if len (large) > len (small): return float (large[0 ]) return (large[0 ] - small[0 ]) / 2.0
滑动窗口的最大值 给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def maxInWindows (self, num, size ): queue,res,i = [],[],0 while size > 0 and i < len (num): if len (queue) > 0 and i - size + 1 > queue[0 ]: queue.pop(0 ) while len (queue) > 0 and num[queue[-1 ]] < num[i]: queue.pop() queue.append(i) if i >= size-1 : res.append(num[queue[0 ]]) i += 1 return res s = Solution() print (s.maxInWindows([2 ,3 ,4 ,2 ,6 ,2 ,5 ,1 ],3 ))
简单问题 替换空格 请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
1 2 3 4 5 class Solution : def replaceSpace (self, s ): s = s.replace(' ' ,'%20' ) return s
用两个栈实现队列 用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def __init__ (self ): self.stack1 = [] self.stack2 = [] def push (self, node ): if len (self.stack1) == 0 : while len (self.stack2): self.stack1.append(self.stack2.pop()) self.stack1.append(node) def pop (self ): if not len (self.stack2) == 0 : return self.stack2.pop() else : while len (self.stack1) > 1 : self.stack2.append(self.stack1.pop()) return self.stack1.pop()
斐波那契数列 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39
1 2 3 4 5 6 7 class Solution : def Fibonacci (self, n ): res=[0 ,1 ,1 ,2 ] while len (res)<=n: res.append(res[-1 ]+res[-2 ]) return res[n]
跳台阶 一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
1 2 3 4 5 6 7 8 9 class Solution : def jumpFloor (self, number ): if number <= 2 : return number else : a = b = 1 for _ in range (number-1 ): a,b = b , a+b return b
矩形覆盖 我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
1 2 3 4 5 6 class Solution : def rectCover (self, number ): res = [0 ,1 ,2 ] while len (res) <= number: res.append(res[-1 ] + res[-2 ]) return res[number]
二进制中1的个数 输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
1 2 3 4 5 class Solution : def NumberOf1 (self, n ): return bin (n).count("1" ) if n>=0 else bin (2 **32 +n).count("1" )
反转链表 输入一个链表,反转链表后,输出新链表的表头。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def ReverseList (self, pHead ): if not pHead: return None p = pHead j = p.next p.next = None while j: pHead = j j = j.next pHead.next = p p = pHead return pHead
合并两个排序的链表 输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def Merge (self, pHead1, pHead2 ): dummy = p = ListNode(None ) while pHead1 and pHead2: if pHead1.val > pHead2.val: p.next = pHead2 pHead2 = pHead2.next else : p.next = pHead1 pHead1 = pHead1.next p = p.next p.next = pHead1 or pHead2 return dummy.next
二叉树的镜像 操作给定的二叉树,将其变换为源二叉树的镜像。
1 2 3 4 5 6 7 8 9 10 11 12 二叉树的镜像定义:源二叉树 8 / \ 6 10 / \ / \ 5 7 9 11 镜像二叉树 8 / \ 10 6 / \ / \ 11 9 7 5
1 2 3 4 5 6 7 8 9 class Solution : def Mirror (self, root ): if not root: return None else : root.left,root.right = root.right,root.left self.Mirror(root.left) self.Mirror(root.right) return root
最小的K个数 输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def insert_sort (self,li,val ): li.append(val) idx = len (li) -1 while idx >= 1 and li[idx-1 ] > li[idx]: li[idx],li[idx-1 ] = li[idx-1 ],li[idx] idx -= 1 return li[:-1 ] def GetLeastNumbers_Solution (self, tinput, k ): if len (tinput) < k or k == 0 : return [] li = [float ('inf' )] * k for num in tinput: if num < li[-1 ]: li = self.insert_sort(li,num) return li
第一个只出现一次的字符 在一个字符串(0<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1(需要区分大小写).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def FirstNotRepeatingChar (self, s ): idx_list = [0 ] * 58 mapping = {} for idx in range (len (s)): if s[idx] in mapping: mapping[s[idx]] += 1 else : mapping[s[idx]] = 1 idx_list[ord (s[idx])-65 ] = idx res = float ('inf' ) for char,count in mapping.items(): if count == 1 : res = min (res,idx_list[ord (char)-65 ]) return res if res != float ('inf' ) else -1
两个链表的第一个公共结点 输入两个链表,找出它们的第一个公共结点。
1 2 3 4 5 6 7 class Solution : def FindFirstCommonNode (self, pHead1, pHead2 ): p1,p2=pHead1,pHead2 while p1 != p2: p1 = p1.next if p1 else pHead2 p2 = p2.next if p2 else pHead1 return p1
数字在排序数组中出现的次数 统计一个数字在排序数组中出现的次数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def find_count (self,data,idx,k ): res = 1 left = idx - 1 right = idx + 1 while left >= 0 and data[left] == k: res += 1 left -= 1 while right <= len (data) - 1 and data[right] == k: res += 1 right += 1 return res def GetNumberOfK (self, data, k ): left = 0 right = len (data) while left < right: mid = left + (right - left) // 2 if data[mid] > k: right = mid elif data[mid] < k: left = mid + 1 else : return self.find_count(data,mid,k) return 0
二叉树的深度 输入一棵二叉树,求该树的深度。
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径, 最长路径的长度为树的深度。
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def TreeDepth (self, pRoot ): if not pRoot: return 0 else : a = b = 1 if pRoot.left: a = 1 + self.TreeDepth(pRoot.left) if pRoot.right: b = 1 + self.TreeDepth(pRoot.right) return max (a,b)
平衡二叉树 输入一棵二叉树,判断该二叉树是否是平衡二叉树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def TreeDepth (self, pRoot ): if not pRoot: return 0 else : a = b = 1 if pRoot.left: a = 1 + self.TreeDepth(pRoot.left) if pRoot.right: b = 1 + self.TreeDepth(pRoot.right) return max (a,b) def IsBalanced_Solution (self, pRoot ): if not pRoot: return True else : if abs (self.TreeDepth(pRoot.left) - self.TreeDepth(pRoot.right)) <= 1 : a = self.IsBalanced_Solution(pRoot.left) b = self.IsBalanced_Solution(pRoot.right) return a and b else : return False
进阶方法 :
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def IsBalanced (self, pRoot, depth ): if pRoot is None : return True if self.IsBalanced(pRoot.right, right) and self.IsBalanced(pRoot.left, left): diff = abs (left - right) if diff <= 1 : depth = max (left, right) +1 return True return False def IsBalanced_Solution (self, pRoot ): depth = 0 return self.IsBalanced(pRoot, depth)
和为S的两个数字 输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def FindNumbersWithSum (self, array, tsum ): left = 0 right = len (array) - 1 while left < right: tot = array[left] + array[right] if tot < tsum: left += 1 elif tot > tsum: right -= 1 else : return array[left],array[right] return [] s = Solution() print (s.FindNumbersWithSum([1 ,2 ,4 ,7 ,11 ,15 ],15 ))
左旋转字符串 对于一个给定的字符序列S,请你把其循环左移K位后的序列输出。例如,字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果,即“XYZdefabc”。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def LeftRotateString (self, s, n ): if not s: return '' leng = len (s) n %= leng for _ in range (n): s = s[1 :] + s[0 ] return s s = Solution() print (s.LeftRotateString('123456' ,7 ))
或者:
1 2 3 4 5 6 7 8 9 10 11 class Solution : def LeftRotateString (self, s, n ): if not s: return '' n %= len (s) return s[n:]+s[:n] s = Solution() print (s.LeftRotateString('123456' ,7 ))
翻转单词顺序列 “student. a am I”。把句子单词的顺序翻转,正确的句子应该是“I am a student.”。
1 2 3 4 5 6 7 8 9 class Solution : def ReverseSentence (self, s ): res = '' for char in s.split(' ' )[::-1 ]: res += (char + ' ' ) return res[:-1 ] s = Solution() print (s.ReverseSentence('student. a am I' ))
或者 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def ReverseSentence (self, s ): word_start = word_end = len (s) - 1 res = '' while word_start >= 0 : if s[word_start] != ' ' : word_start -= 1 else : res += s[word_start:word_end+1 ] word_start -= 1 word_end = word_start res += ' ' + s[word_start+1 :word_end+1 ] return res[1 :] s = Solution() print (s.ReverseSentence('student. a am I' ))
约瑟夫环 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def LastRemaining_Solution (self, n, m ): if not n: return -1 start = 0 l = list (range (n)) while len (l) != 1 : k = (m + start - 1 ) % n l.pop(k) n -= 1 start = k return l[0 ] s = Solution() print (s.LastRemaining_Solution(5 ,1 ))
把二叉树打印成多行 从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def Print (self, pRoot ): if not pRoot: return [] res = [] q = [pRoot] while q: res.append([node.val for node in q]) tmp = [] for node in q: if node.left: tmp.append(node.left) if node.right: tmp.append(node.right) q = tmp return res