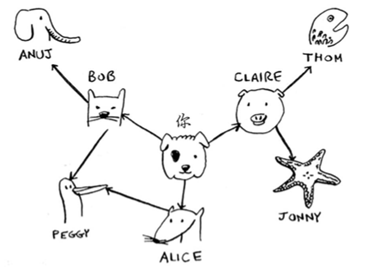
使用散列表实现图

1
2
3
4
5
6
7
8
9
10
neighbor = {}

neighbor['you'] = ['alice','bob','claire']
neighbor['bob'] = ['anuj','peggy']
neighbor['alice'] = ['peggy']
neighbor['claire'] = ['thom','jonny']
neighbor['anuj'] = []
neighbor['peggy'] = []
neighbor['thom'] = []
neighbor['jonny'] = []

1562042102949

广度优先的复杂度为O(边数+人数)，简记为O(V+E)

任务A依赖于任务B，任务A就必须在任务B后面。这被称为拓扑排序

狄克斯特拉算法

  • 适用 : 非负权重有向无环图
  • 作用 : 起点到各个节点的最短距离

需要三个字典和一个数组：

  1. 一个嵌套字典用于模拟图。
  2. 一个字典用于存储起点到每个节点的开销。
  3. 一个字典用于存储每个节点的父节点。
  4. 一个数组用于存储处理过的节点。

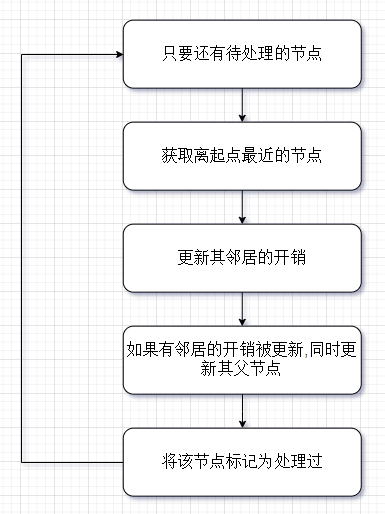
处理逻辑:

1562154682980

得到:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
class Dijkstra:
    def __init__(self,graph,start):
        # 模拟图
        self.graph = graph
        # 开销表
        self.costs = {}
        # 父节点表
        self.parents = {}
        # 已处理列表
        self.processed = []
        # 起点
        self.start = start

    # 每个节点到起点的开销表
    def create_costs_dict(self):
        for nodes,weight in self.graph[self.start].items():
            self.costs[nodes] = weight

    # 每个节点的父节点
    def create_parents_dict(self):
        for nodes in self.graph[self.start]:
            self.parents[nodes] = self.start
        

    def find_lowest_cost_node(self):
        '''
        接受开销表为函数参数,返回开销最低的节点
        '''
        lowest_cost = float('inf')
        lowest_cost_node = None

        for node in self.costs:
            val = self.costs.get(node)
            if val < lowest_cost and node not in self.processed:
                lowest_cost = val
                lowest_cost_node = node
        return lowest_cost_node


    def show_tot_route(self):
        reverse_dict = dict(zip(self.parents.values(),self.parents.keys()))
        next_node = self.start
        res = self.start + ' '

        while reverse_dict.get(next_node):
            next_node = reverse_dict.get(next_node)
            res += f'-> {next_node} '

        return res

    def run(self):
        self.create_costs_dict()
        self.create_parents_dict()

        while len(self.processed) != len(self.costs):
            # 便宜节点
            lowest_cost_node = self.find_lowest_cost_node()
            next_nodes = graph[lowest_cost_node]  # {'a': 3, 'fin': 5}

            # 便宜节点到下一个节点的权重
            for neighbor,weight in next_nodes.items():
                new_costs = self.costs[lowest_cost_node] + weight

                if self.costs.get(neighbor):
                    if self.costs[neighbor] > new_costs:
                        self.costs[neighbor] = new_costs
                        # 更新父节点
                        self.parents[neighbor] = lowest_cost_node
                else:
                    self.costs[neighbor] = new_costs
                    # # 更新父节点
                    self.parents[neighbor] = lowest_cost_node
            self.processed.append(lowest_cost_node) 

        route = self.show_tot_route()

        msg = '{:<13}: {}\n{:<13}: {}\n{:<13}: {}'.format('CostsTable',self.costs,
                                                           'ParentsTable',self.parents,
                                                           'Route',route)
        return msg


if __name__ == '__main__':
    graph = {}
    graph['1'] = {}
    graph['1']['2'] = 1
    graph['1']['3'] = 12

    graph['2'] = {}
    graph['2']['4'] = 3
    graph['2']['3'] = 9

    graph['3'] = {}
    graph['3']['5'] = 5

    graph['4'] = {}
    graph['4']['3'] = 4
    graph['4']['5'] = 13
    graph['4']['6'] = 15

    graph['5'] = {}
    graph['5']['6'] = 4

    graph['6'] = {}


    dijkstra = Dijkstra(graph,'1')
    print(dijkstra.run())
    # CostsTable   : {'2': 1, '3': 8, '4': 4, '5': 13, '6': 17}
    # ParentsTable : {'2': '1', '3': '4', '4': '2', '5': '3', '6': '5'}
    # Route        : 1 -> 2 -> 4 -> 3 -> 5 -> 6

动态规划：

将问题分成小问题，先解决小问题，再逐步解决大问题。

反向索引：

搜索引擎的工作原理：
搜索引擎创建一个散列表。这个散列表的键为单词，值为包含指定单词的页面。

现在假设有用户搜索hi，在这种情况下，搜索引擎需要检查哪些页面包含hi。搜索引擎发现页面A和B包含hi，因此将这些页面作为搜索结果呈现给用户。
创建一个散列表，将单词映射到包含它的页面。这种数据结构被称为反向索引（inverted index）。

列表计数比较法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def check(str1,str2):
    list1 = [0]*26
    list2 = [0]*26

    for each_char in str1:
        pos = ord(each_char) - ord('a')
        list1[pos] += 1

    for each_char in str2:
        pos = ord(each_char) - ord('a')
        list2[pos] += 1

    for idx in range(len(list1)):
        if list1[idx] != list2[idx]:
            return False
    return True

if __name__ == '__main__':
    str1 = 'heart'
    str2 = 'earthw'
    print(check(str1,str2))

同理可以延伸出字典比较:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def check(str1,str2):
	all_char_set = set(str1) | set(str2)
	all_char_dict1 = dict.fromkeys(all_char_set,0)
	all_char_dict2 = dict.fromkeys(all_char_set,0)

	for each_char in str1:
		all_char_dict1[each_char] += 1

	for each_char in str2:
		all_char_dict2[each_char] += 1

	return all_char_dict1 == all_char_dict2

if __name__ == '__main__':
	str1 = 'heart'
	str2 = 'earth'
	print(check(str1,str2))

列表的contains操作符是O(n)，字典的contains操作符是O(1)

凡是要==反转项的顺序==,都要想到栈

栈的方法

  1. Stack()创建一个空的新栈。它不需要参数，并返回一个空栈。
  2. push(item)将一个新项添加到栈的顶部。它需要item做参数并不返回任何内容。
  3. pop()从栈中删除顶部项。它不需要参数并返回item。栈被修改。
  4. peek()从栈返回顶部项，但不会删除它。不需要参数。不修改栈。
  5. isEmpty()测试栈是否为空。不需要参数，并返回布尔值。
  6. size()返回栈中的item数量。不需要参数，并返回一个整数。

二分法

  1. 左闭右开
  2. mid = low + (high - low) // 2
  3. high = mid
  4. return low
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def searchInsert(self, nums, target) -> int:
        low = 0
        # 左闭右开
        # 唯一注意:这里是len(nums),不是len(nums)-1
        high = len(nums)
        while low < high:
            # # 注意这里的mid取值
            mid = low + (high - low)//2
            if nums[mid] > target:
                high = mid
            elif nums[mid] < target:
                low = mid + 1
            else:
                return mid
        return low

map抽象数据类型

  1. Map()创建一个新的map。它返回一个空的map集合。
  2. put(key，val)向map中添加一个新的键值对。如果键已经在map中，那么用新值替换旧值。
  3. get(key)给定一个键，获取存储在map中的值或None。
  4. del()使用del map[key]形式的语句从map中删除键值对。
  5. len()返回存储在map中的键值对的数量。
  6. in()对于key in ma语句，如果给定的键在map中返回True，否则为False。