第七章：图

\1. 图是比树更通用的结构;实际上你可以认为树是一种特殊的图。

\2. 图的组成部分:

a) 顶点：顶点（也称为“节点”）是图的基本部分。它可以有一个名称，我们将称为“键”。
一个顶点也可能有额外的信息。我们将这个附加信息称为“有效载荷”。

b) 边：边（也称为“弧”）是图的另一个基本部分。边连接两个顶点，以表明它们之间存在关系。边可以是单向的或双向的。如果图中的边都是单向的，我们称该图是有向图。

c) 权重：边可以被加权以示出从一个顶点到另一个顶点的成本。例如，在将一个城市连接到另一个城市的道路的图表中，边上的权重可以表示两个城市之间的距离。

d) 路径：图中的路径是由边连接的顶点序列。

\3. 对于图G，V是一组顶点，E是一组边。使用G=(V，E)表示。
每个边是一个元组(v，w)，其中w,v∈V。可以添加第三个组件到边元组来表示权重。
子图s是边e和顶点v的集合，使得e⊂E和v⊂V。

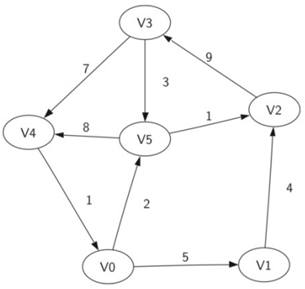
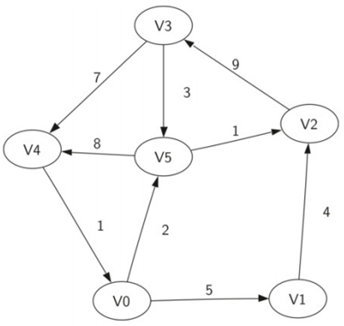
上图就是：
V={V0,V1,V2,V3,V4,V5}
E={(v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v4,v0,1),(v0,v5,2),(v5,v4,8),(v3,v5,3),(v5,v2,1)}

\4. 图抽象数据类型定义如下：

a) Graph()创建一个新的空图。

b) addVertex(vert)向图中添加顶点实例。

c) addEdge(fromVert,toVert)向连接两个顶点的图添加新的有向边。

d) addEdge(fromVert,toVert,weight)向连接两个顶点的图添加新的加权有向边。

e) getVertex(vertKey)在图中获取名为vertKey的顶点。

f) getVertices()返回图中所有顶点的列表。

g) in如果vertexingraph里给定的顶点在图中返回True，否则返回False。

\5. 有几种方法可以在Python中实现图，下面介绍两个很重要的图的实现：邻接矩阵和邻接表。

\6. 邻接矩阵：
实现图的最简单的方法之一是使用二维矩阵。
在该矩阵实现中，每个行和列表示图中的顶点。存储在行v和列w的交叉点处的单元中的值表示是否存在从顶点v到顶点w的边（或者是边的权重）。当两个顶点通过边连接，它们就是相邻的。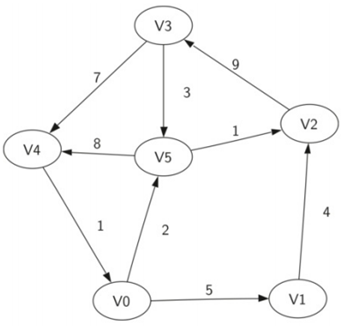

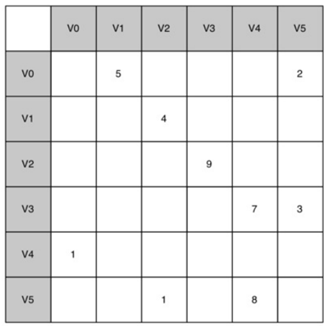
邻接矩阵的优点是简单，对于小图，很容易看到哪些节点连接到其他节点。
然而，注意矩阵中的大多数单元格是空的。所以我们称这个矩阵是“稀疏的”。矩阵不是一种非常有效的方式来存储稀疏数据。
所以说，当边的数量较大时，邻接矩阵是图的良好实现。
当每个顶点连接到每个其他顶点时，矩阵是满的。也就是把矩阵的|V|^2个单元格都填满的情况下，使用邻接矩阵是一个很好的实现。

\7. 邻接表：
实现稀疏连接图的空间高效的方法是使用邻接表
在邻接表，我们保存图中的所有顶点的主列表，然后图中的每个顶点对象维护连接到的其他顶点的列表。在顶点类中，我们将使用字典，其中键是顶点，值是权重。

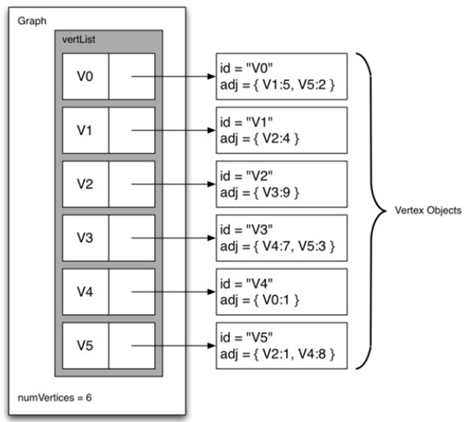
简单来说：
邻接表就是一个列表，列表的元素是每个顶点对应的顶点类，这个顶点类有一个字典，那个字典就是存储了该顶点到其他顶点的权重。

\8. 邻接矩阵和邻接表的区别：

a) 邻居矩阵简单，但空间效率低。

b) 邻接表能紧凑地表示稀疏图，容易找到直接连接到特定顶点的所有链接。

\9. 实现邻接表：


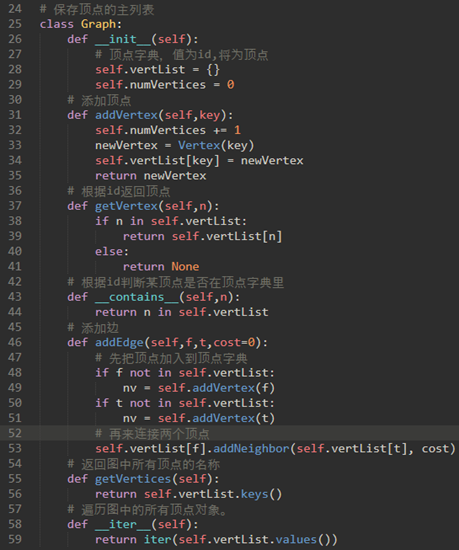
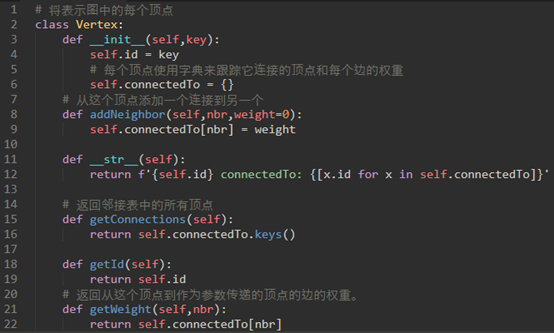
简单使用，模拟下面的图：


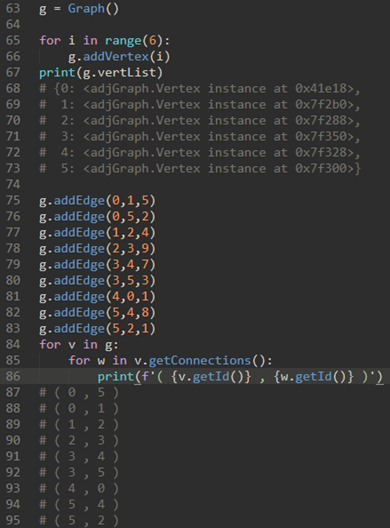
简单来说，邻接表的思想就是：

a) 使用Vertex类模拟点，该类维护了点的性质和功能

b) 使用Graph类模拟图，该类维护了图的性质和功能

\10. 字梯的问题：
将单词“FOOL”转换为单词“SAGE”。
在字梯中每次改变一个字母，将一个单词变换成另一个单词。
FOOL→POOL→POLL→POLE→PALE→SALE→SAGE

计算起始单词转换为结束单词所需的最小转换次数。步骤：

a) 将单词之间的关系表示为图。

b) 使用广度优先搜索的图算法来找到从起始单词到结束单词的有效路径。

\11. 我们的第一个问题是弄清楚如何将大量的单词集合转换为图。
如果两个词只有一个字母不同，我们就创建从一个词到另一个词的边。

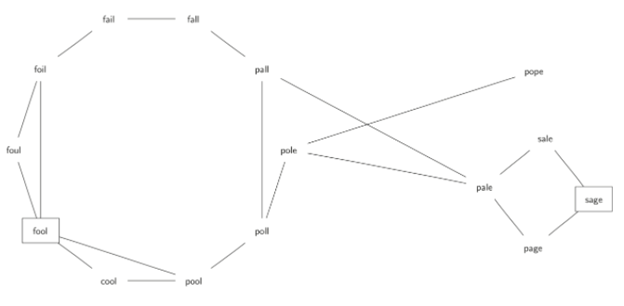
我们的第一思路是：
为每个单词创建一个顶点。比较列表中的每个单词。如果所讨论的两个字只有一个字母不同，在图中创建它们之间的边。
上面的方法的复杂度为O(n^2)。太差。

现在使用下面的方法：
建立四个列表，每个列表都有一个匹配模式，当某个单词能匹配成功，就放进这个列表里。
一旦我们把所有单词放到适当的列表中，就知道列表中的所有单词必须连接。

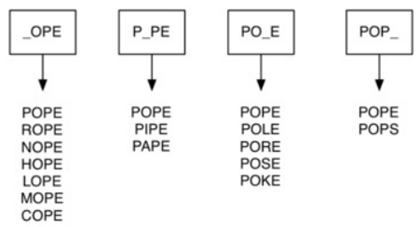
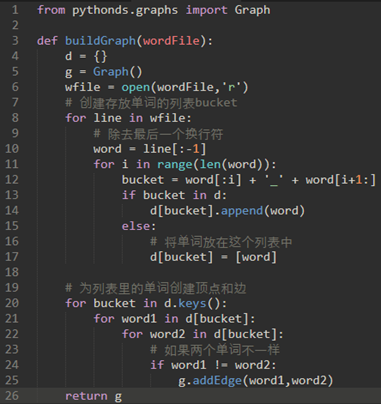
\12. 使用字典来实现刚才描述的方案。
字典的键就是匹配模式，值就是单词列表。
(重要)为图中的每个单词创建一个顶点。然后，在字典中的相同键下找到的所有顶点创建边。

\13. 广度优先搜索：来找到字梯问题的最短解。
广度优先搜索先从其他起始顶点开始添加它的所有子节点，然后再添加其子节点的子节点。
广度优先搜索算法就像在建一棵树，一次建一层

我们在算法图解里的代码如下：
在你的关系网中寻找愿意借你钱的人。

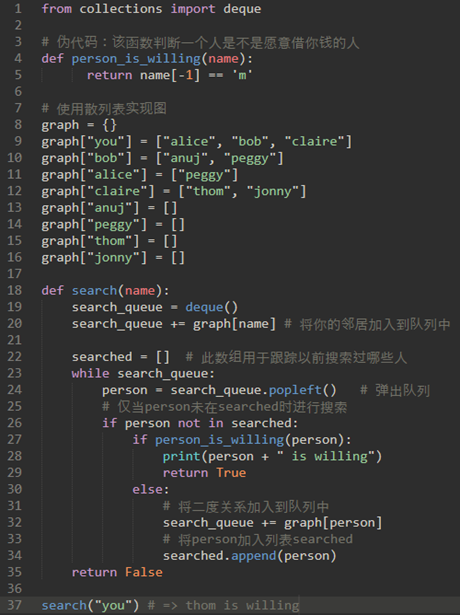
在这里，我们使用了一个列表searched来存储搜索过的人。
现在我们可以定义一个类，并且使用颜色来区分搜索过的人。

为了跟踪进度，BFS将每个顶点着色为白色，灰色或黑色。

a) 当图被构造时，所有顶点被初始化为白色。白色顶点是未发现的顶点。

b) 当一个顶点最初被发现时它变成灰色的
(下次别的点搜索到这个点时，发现是灰色就说明已经被发现了，就不会再进行搜索了)，

c) 当BFS完全探索完一个顶点时，它被染成黑色。
这意味着一旦顶点变黑色，就没有与它相邻的白色顶点。另一方面，如果一个顶点被标识为了灰色，这就意味着其附近可能还存在着未探索的顶点(白色顶点)等待被探索。

简单来说：

a) 白色为尚未探索的点

b) 灰色为正在探索的点

c) 黑色为探索完毕的点

广度优先搜索算法使用邻接表来实现图。此外，它还使用了一个队列来决定下一步应该探索哪一个顶点。

队列的作用：扫描到一个顶点，会把该顶点添加到队尾。由于队列的后进后出。只有当把距离为k的顶点都从队列中弹出完了以后，队首才会是距离为k+1的顶点，然后接着把距离为k+2的顶点扫到队尾。

BFS算法使用Vertex类的扩展版本。这个新的顶点类添加了三个新的实例变量：
distance（距离），
predecessor（前导）（父顶点）
color（颜色）。
这些实例变量中的每一个还具有适当的getter和setter方法。
(这个扩展的顶点类代码包含在pythonds包中)

\14. 广度优先搜索从起始顶点s开始，此时s的颜色被设置为灰色，代表它现在已经被发现了，另外两个参数——距离和父顶点，对于起始节点s初始设置为了0和None。
随后，起始节点会被加入到一个队列中，下一步便是系统地探索队首顶点。这个过程通过遍历队首顶点的邻接列表来完成，每检查邻接表中的一个顶点，便会维护这个顶点的颜色参量，如果颜色是白色的，就说明这个节点尚未被探索，也就会按下述四步操作：

a) 把这个新的未探索的节点nbr，标记为灰色；

b) nbr的父顶点被设置为当前节点currentVert；
（比如，我是从a点向下搜索到了b点，那么a就为b的父节点）

c) nbr的距离被设置为当前节点的距离加一；
（比如从顶点s到a的距离是sa，那么从顶点s到b的距离一定是sa+1.）

d) nbr被加入队尾，直到在当前顶点的邻接列表中的所有顶点nbr被搜索完后，才能够进行下一层次的探索操作。

假设队列的队首顶点是a，a到顶点的距离是sa，那么，会在搜索完a的下一层的所有距离为sa+1的顶点。把a的颜色标记为黑色。弹出a。此时a后面的节点变为队首。

若a2距离顶点的距离一样等于sa，那么也会搜索完a2的下一层所有距离为sa+1的顶点。

这样循环下去。

\15. 代码如下：

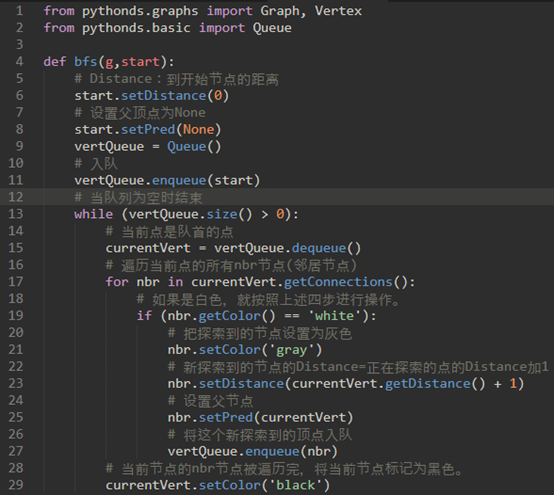
注意这里21行是很有必要的，因为某个顶点很有可能会被重复探索，就会重复加入队列当中。我们之前是使用一个列表来存储已经探索过的点（13里有代码），现在改用颜色属性来区别。

实际上，如果在探索的时候发现顶点改变为灰色，这表明有一条较短的路径到该顶点。
所以，所有顶点都被扩展之后对应的图为：


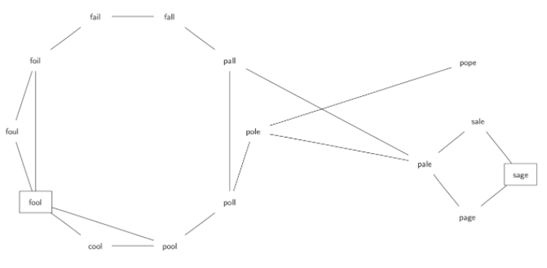
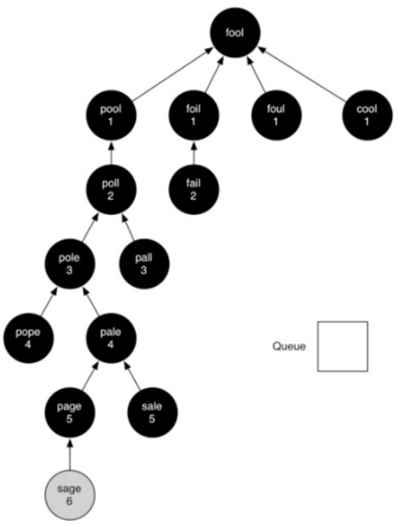
和之前学的一样，广度优先搜索能计算出跟顶点到其他所有点的最短路径。这时就可以定义一个方法来实现：

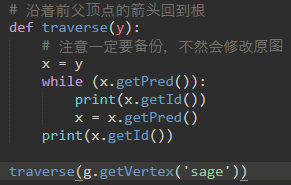
\16. 广度优先搜索分析：
因为一个顶点必须是白色，才能被检查和添加到队列，所以每个顶点|V|最多执行一次while循环。所以while循环为O(v)。
每个顶点最多被出列一次，并且仅当节点u出队时，我们才检查从节点u到节点v的边。所以嵌套在while内部的for循环对于图中的每个边执行最多一次，为|E|。这给出了用于for循环的O(E)。
组合这两个环路得出广度优先搜索为O(V+E)。

或者可以这么理解：
在图中爬行，就意味着你将沿着每条边前行。因此此操作为O(边数)。
同时，你又需要将每个顶点都添加进队列，添加一个顶点为O(1)，所以此操作为O(顶点数)。
所以广度优先的复杂度为O(边数+顶点数)。

因此复杂度为O(边数+顶点数)，简记为O(V+E)
其中V为顶点数，E为边数。

\17. 骑士之旅：
国际象棋上有一个马，任务是找到一系列的动作，让马跳遍棋盘上的每个单元格，每个单元格能且仅能跳一次。

我们将使用两个主要步骤解决问题：

a) 表示骑士在棋盘上作为图的动作。

b) 使用图算法来查找长度为rows×columns-1的路径，其中图上的每个顶点都被访问一次。

\18. 为了将骑士的旅游问题表示为图，规定：

a) 棋盘上的每个单元格表示为图中的一个节点。

b) 骑士的每个合法移动表示为图形中的边。

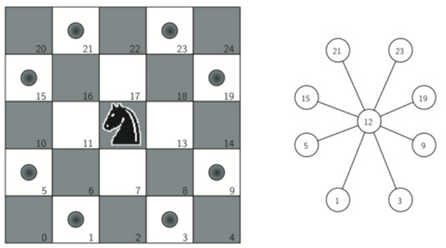
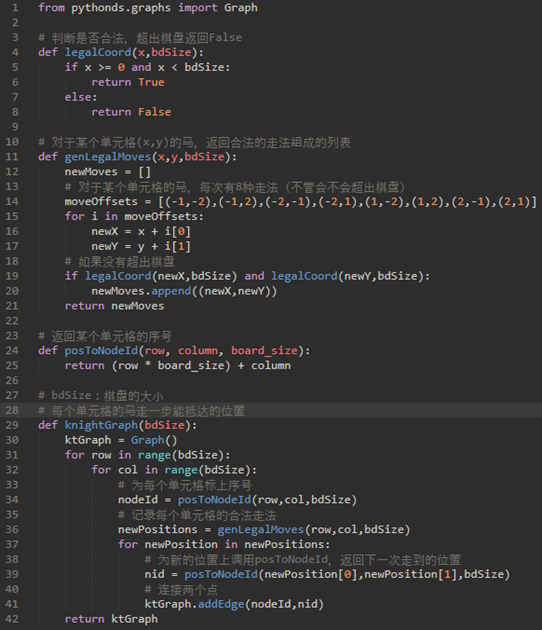
knightGraph函数的功能就是：每一个单元格走一步能抵达的位置组成的图。
也就是说：为棋盘上的每一个位置创建一个移动列表。所有移动在图形中转换为边。
（eg:单元格0能连接的顶点只有17和10）

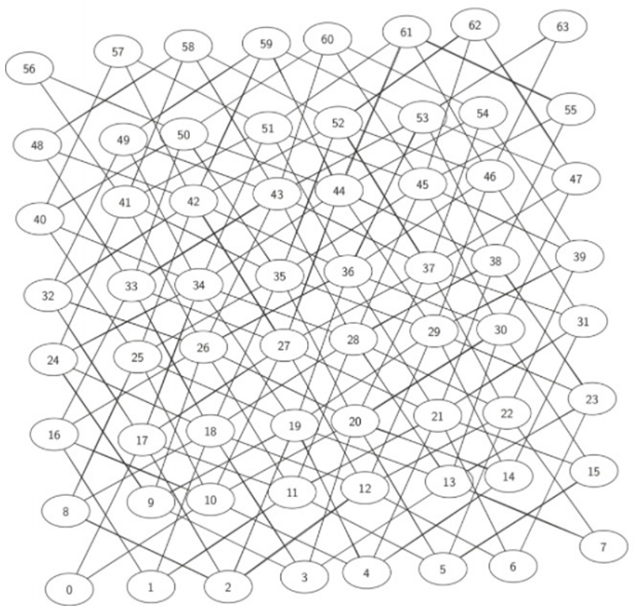
这样，我们就使用创建knightGraph函数了一个64顶点，336边的图。如果使用邻接矩阵，那么就会有4096（64*64）个单元格，由于只有336个边，邻接矩阵只有8.2％填充率。

\19. 深度优先搜索：使用深度有效搜索来处理骑士之旅问题。
深度优先搜索通过尽可能深地探索树的一个分支来创建搜索树。

介绍实现深度优先搜索的两种算法。

a) 第一种实现通过明确地禁止一个节点被多次访问来直接解决骑士的旅行问题。

b) 第二种实现是更通用的，允许在构建树时多次访问节点。(第二种实现可以用于开发其他图形算法)

\20. 骑士问题是让马遍历棋盘各个单元格一次，就是说，需要找出一个64顶点，共计63边的路径

knightTour函数有四个参数：

a) n，搜索树中的当前深度;

b) path，到此为止访问的顶点的列表;

c) u，图中我们希望探索的顶点;

d) limit路径中的节点数。

（重要）深度优先算法(DFS)一定是递归的。

a) 基线条件：当调用knightTour函数时，它首先检查基本情况。如果我们有一个包含64个顶点的路径，我们状态为True的knightTour返回，表示我们找到了一个成功的线路。

b) 递归条件：如果路径不够长，我们继续通过选择一个新的顶点来探索一层，并对这个顶点递归调用knightTour。

\21. 使用颜色来跟踪图中的哪些顶点已被访问。

a) 未访问的顶点是白色的，

b) 已访问的顶点是灰色的。

如果已经探索了特定顶点的所有邻居，并且我们尚未达到64个顶点的目标长度，我们已经到达死胡同。当我们到达死胡同时，我们必须回溯。当我们从状态为False的knightTour返回时，发生回溯。
在广度优先搜索中，我们使用一个队列来跟踪下一个要访问的顶点。由于深度优先搜索是递归的，我们隐式使用一个栈来帮助我们回溯。

代码如下：

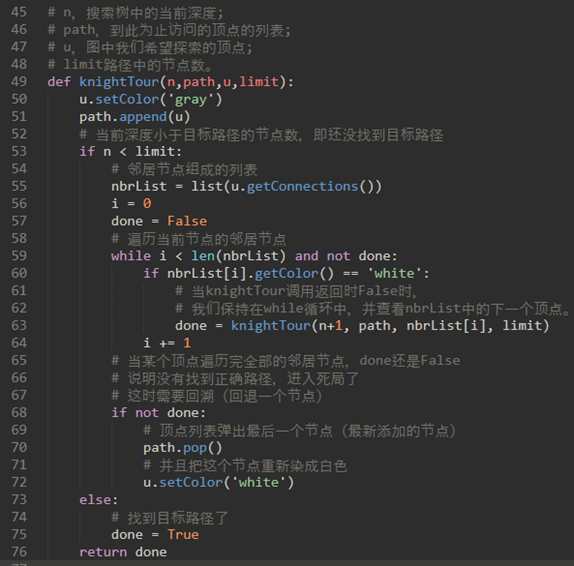
对于上面的代码我们将使用简化成6个顶点的示意图的形式讲解。
目标是从A走到C，遍历全部6个节点：

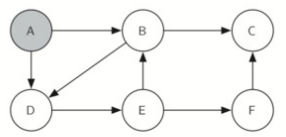
一开始走路径ABC：

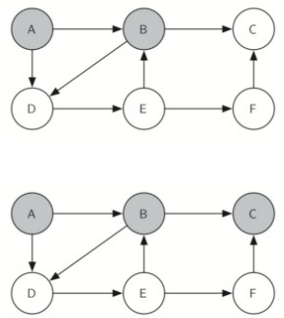
节点C是没有相邻节点的死胡同。此时，我们将节点C的颜色更改为白色。对knightTour的调用返回值False。从递归调用的返回有效地将搜索回溯到顶点B

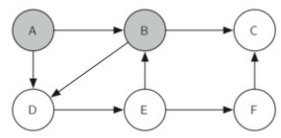
接着继续遍历B的邻居节点，因为刚刚走过了C，这次走D。经过E，F点，直到再次到达节点C。

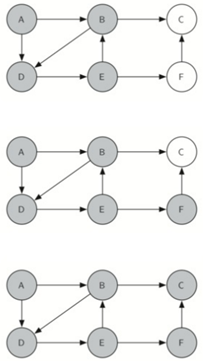
当我们到达节点C时，测试n<limit失败，所以我们知道已经耗尽了图中的所有节点。在这一点上，我们可以返回True，表示我们已经成功地浏览了图。当我们返回列表时，路径具有值[A，B，D，E，F，C]，这是我们需要遍历图以访问每个节点的顺序。

\22. 骑士之旅分析：
复杂度为O(k^N)的指数算法。其中N是棋盘上的方格数，k是小常数。
原因很简单：我们在while循环里用了递归。

运用高中数学，这其实是一个分步完成。（eg:第一步有3种可能，第二步有4中可能，所以总共有3*4=12种可能）
骑士问题也一样，第一步有8种可能，第二步有3种可能…
画成图就是一个63层庞大的树。

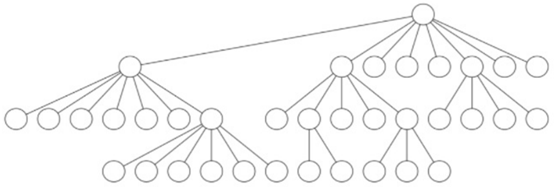
高度N的二叉树中的节点数量是2^N+1-1。而这个是最多多达八个孩子的树。
因为每个节点的分支因子是可变的，我们可以使用平均分支因子估计节点的数量。
对于常规的8x8棋盘，平均分支因子k=5.25，所以总共有1.3×10^46个节点。

其实，上面的算法是往大里算了的，实际比这个小一些。因为当进入死局的时候，直接就回溯了，并没有走完64个节点。

\23. 就像上面说的，每个节点的分支因子是可变的（2-8个），也就是说不同单元格的下一步走法的数量是不一样的。最边角的单元格只有2种走法，中间的单元格有8种走法。

既然如此，我们就可以设计函数来优化：让马先走那些‘走法较少’的单元格（也就是先走边缘的单元格）。
为什么这种算法可以加速？
这么理解。我们将棋盘分成左中右三部分，如果我们先走中间的部分，接着走右边的部分，那么因为跨度太大，我们将不能到达左边的部分。
如果先走边缘，我们就能够尽早地访问难以到达的角落。
利用这种知识加速算法被称为启发式。

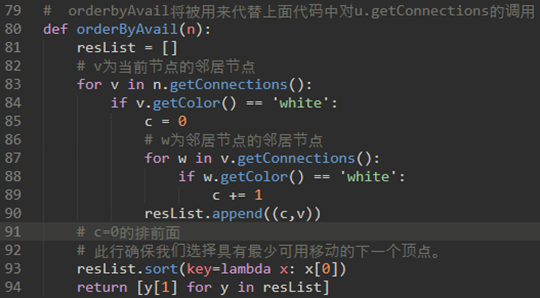
上面orderbyAvail函数用于代替55行的u.getConnections函数。
上面的代码就是说：
当走完一步后，再下一步有多种走法的节点，后面再来测。
当走完一步后，再下一步走法少的节点，先测。

上面代码很好理解，当走完一步后，再下一步有多种走法的节点，都是中间的节点；当走完一步后，再下一步走法少的节点，是边缘的节点。这样我们就确保了先走边缘的节点了。

\24. 通用深度优先搜索：
骑士之旅是深度优先搜索的特殊情况，其目的是创建最深的第一棵树，没有任何分支。
更一般的深度优先搜索实际上更容易。它的目标是尽可能深的搜索，在图中连接尽可能多的节点，并在必要时创建分支。

甚至可能的是，深度优先搜索将创建多于一个树。当深度优先搜索算法创建一组树时，我们称之为深度优先森林。

与广度优先搜索一样，我们的深度优先搜索使用前导(就是父节点)链接来构造树。
在深度优先搜索，Vertex类有多两个属性：discovery和finish。
发现时间是首次遇到顶点之前的步骤数。
完成时间是顶点着色为黑色之前的步骤数。

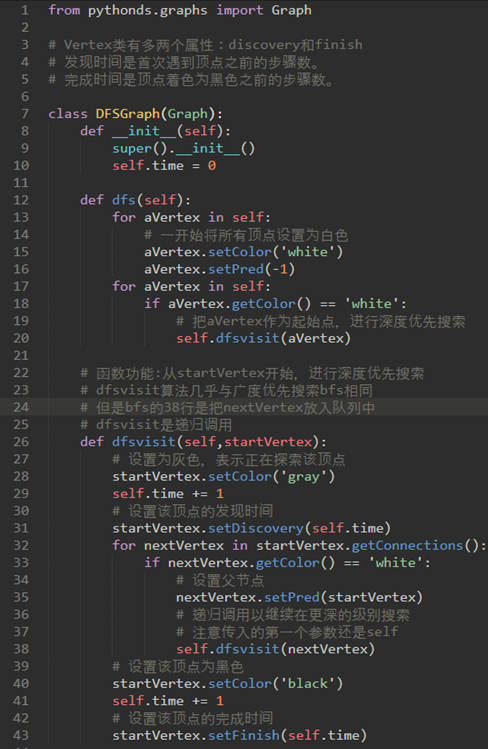
注意38，在for循环里递归调用dfsvisit方法。
注意29的self.time是图的属性，不过是使用setDiscovery和setFinish方法将self.time赋予顶点。

\25. 下面是上面代码的执行示意图：
首先将所有点设置为白色，然后A开始，将A设置为灰色，将A的discovery属性设置为1，然后递归调用dfsvisit，走到B，将B的discovery属性设置为2，再走到C，discovery设置为3。

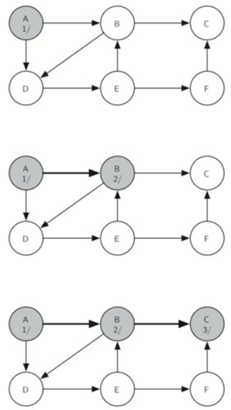
没有与C相邻的顶点。这意味着我们完成了对节点C的探索，因此我们可以将顶点染成黑色，并将完成时间设置为4。

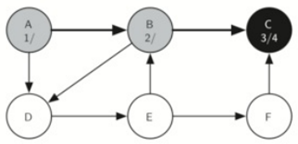
由于顶点C是一个分支的结束，我们现在返回到顶点B，继续探索与B相邻的节点。所以走到D，D指引我们走到E

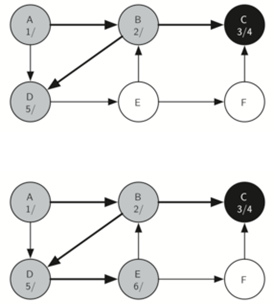
当走到E时，E具有两个相邻的顶点B和F，但是由于B已经是灰色的，所以不会将B置于循环中！因此，继续探索列表中的下一个顶点，即F

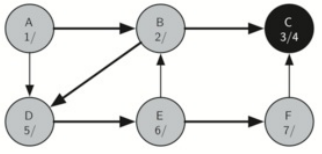
顶点F只有一个相邻的顶点C，但由于C是黑色的，没有别的东西可以探索，算法已经到达另一个分支的结束。所以设置F点的完成时间并且将其标记为黑。

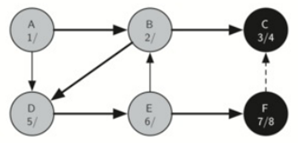
接着，算法就会递归回来，回到第一个节点，每个节点都会设置完成时间并且标记为黑。

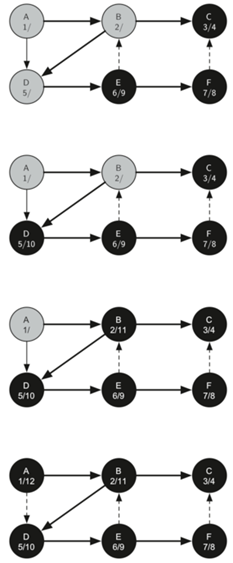
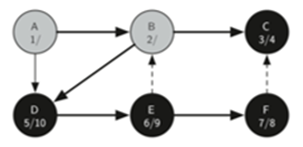
最终结果：

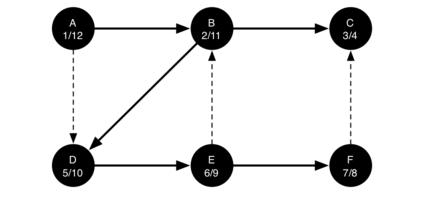
每个节点的开始和结束时间展示一个称为括号属性的属性。
该属性意味着深度优先树中的所有子节点都比他的父节点更晚发现并且更早完成。（因为使用了递归，而递归实际上就是一种栈）

图中的虚线指示检查的边，但是在边的另一端的节点已经被添加到深度优先树。

\26. 深度优先搜索分析：
dfs中的循环都在O(V)中运行，不计入dfsvisit中发生的情况，因为它们对图中的每个顶点执行一次。在dfsvisit中，对当前顶点的邻接表中的每个边执行一次循环。由于只有当顶点为白色时，dfsvisit才被递归调用，所以循环对图中的每个边或O(E)执行最多一次。因此，深度优先搜索的总时间是O(V+E)。

\27. （重要）比较两种深度优先的实现方法：

a) 禁止一个节点被多次访问，创建最深的第一棵树。

b) 允许在构建树时多次访问节点，并且在必要的使用创建分支。


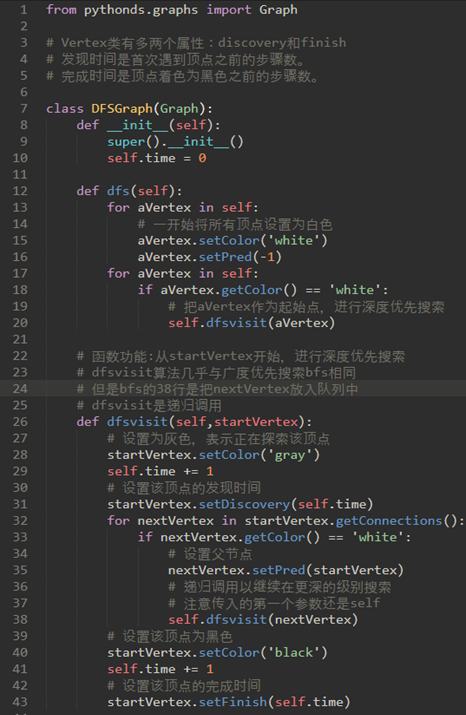
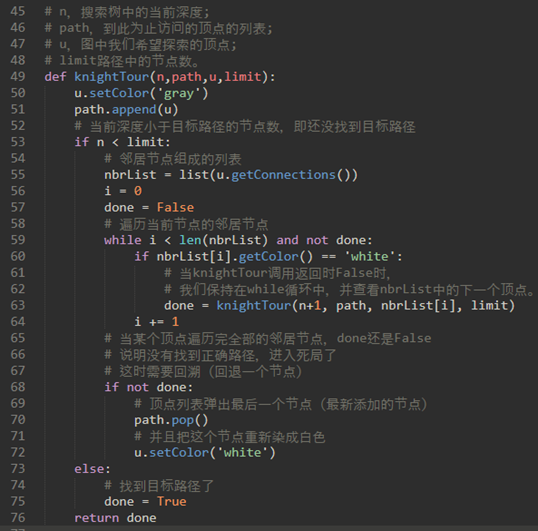
第一种：路径为A-B-D-C-E-F，没有分支

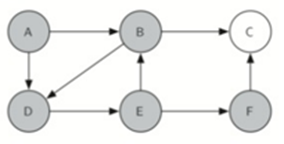
第二种：路径为A-B-D-E-F，B有分支C

通过代码我们知道，第一种方式运用了队列，而第二种方式运用了栈。
第一种方法在走到死路的时候，需要回溯，弹出最后一个节点。
第二种方法在走到死路的时候，直接原地生产分支，然后回到倒数第二个节点前进。

简单来说，两种深度优先代码实现的目的不同：

a) 第一种目的是创建最深的第一棵树，没有任何分支。

b) 第二种目的是尽可能深的搜索，在图中连接尽可能多的节点，并在必要时创建分支。
这种实现被称为“通用深度优先搜索”

\28. 拓扑排序：
现在要制作一批煎饼，菜谱：
1个鸡蛋，1杯煎饼粉，1汤匙油和3/4杯牛奶。

要制作煎饼，你必须加热炉子，将所有的成分混合在一起，勺子搅拌。当开始冒泡，你把它们翻过来，直到他们底部变金黄色。在你吃煎饼之前，你会想要加热一些糖浆。

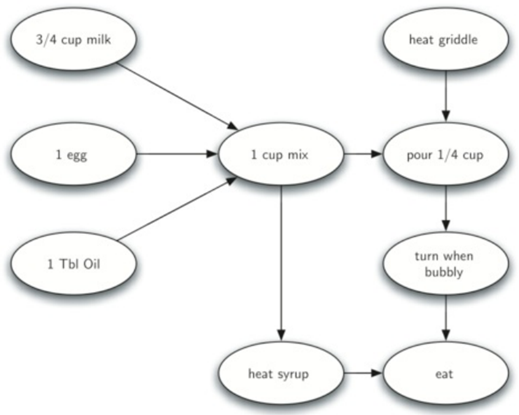
你可以从加热煎饼开始，或通过添加任何成分到煎饼。为了帮助我们决定应该做的每一个步骤的精确顺序，我们转向一个图算法称为拓扑排序。

简单来说，拓扑排序用于指示事件的优先级。

\29. 拓扑排序采用有向无环图，并且产生所有其顶点的线性排序，使得如果图G包含边（v，w），则顶点v在排序中位于顶点w之前。(eg:前面的turn when bubbly一定在eat前面)

\30. 拓扑排序是深度优先搜索的简单的改造。
拓扑排序的算法如下：

a) 对于某些图g调用dfs(g)。
我们想要调用深度优先搜索的主要原因是计算每个顶点的完成时间。

b) 以完成时间的递减顺序将顶点存储在列表中。

c) 返回有序列表作为拓扑排序的结果。

例如上面的例子使用拓扑排序：

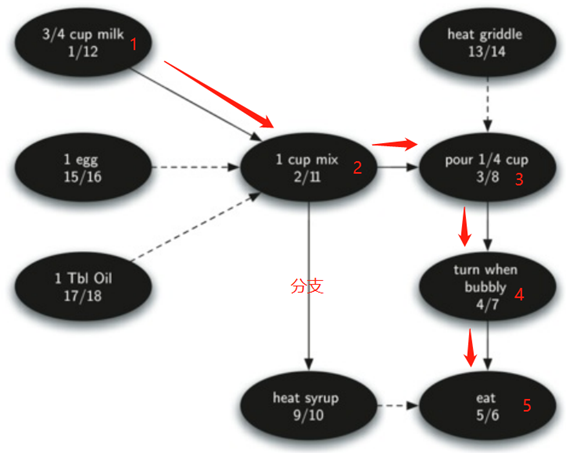
深度优先中的虚线表示检查的边，但是在边的另一端的节点已经被添加到深度优先树。
所以实线就是主要流程，虚线就是补充部分。

将各事件完成时间的递减顺序排列，得出确切的做煎饼的步骤顺序。

\31. 强连通分量：
将万维网变换为图，我们将把一个页面视为一个顶点，并将页面上的超链接作为将一个顶点连接到另一个顶点的边。
那么这个图将十分的庞大。

强连通分量算法（SCC）：帮助我们找到图中高度互连的顶点的集群。

强连通分量是什么意思？
强连通分量实际上指的是一些点的集合，而这个集合的定义就是：任意集合中的点都能到达其他所有同样在集合中的点。
eg:下面图分成三个模块，这三个模块就是三个强连接分量。
点A可以按着箭头走到BCDE四个点，B可以按着箭头走到ACDE四个点，同理CDE也是如此。
也就是说，ABCDE都是互通的，所以ABCDE是一个强连接分量

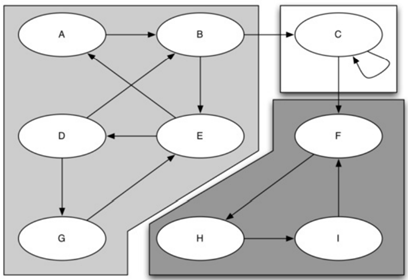
如果要对强连通分量严格定义的话：
我们定义图G的强连通分量C作为顶点C⊂V的最大子集，使得对于每对顶点v,w∈C，我们具有从v到w的路径和从w到v的路径。

\32. 一旦确定了强连通分量，我们就可以通过将一个强连通分量中的所有顶点组合成一个较大的顶点来显示该图的简化视图。

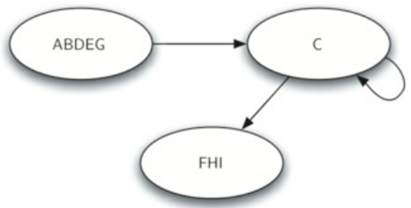
这样，我们就能把互联网简化成小一点的图了。

\33. 图的转置：反转图中的所有的边。
图G的转置被定义为图G^T。

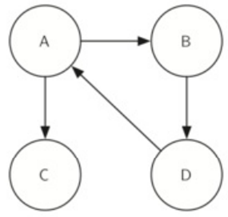
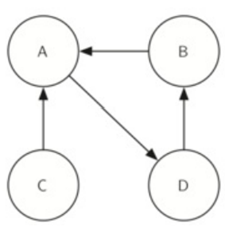
也就是说，如果在原始图中存在从节点A到节点B的有向边，则G^T将包含从节点B到节点A的边

\34. 上面左图G，ABCD是一个强连通分量，在转置之后，图G^T也是一个强连通分量。

我们现在得出用于计算图的强连通分量的算法。

a) 调用dfs为图G计算每个顶点的完成时间。

b) 计算G^T。

c) 为图G^T调用dfs，但在DFS的主循环中，以完成时间的递减顺序探查每个顶点。

d) 在步骤3中计算的森林中的每个树是强连通分量。输出森林中每个树中每个顶点的顶点标识组件。

下面图一为原始图使用dfs算法得出的的开始和结束时间。图二为转置图使用dfs算法得出的的开始和结束时间。


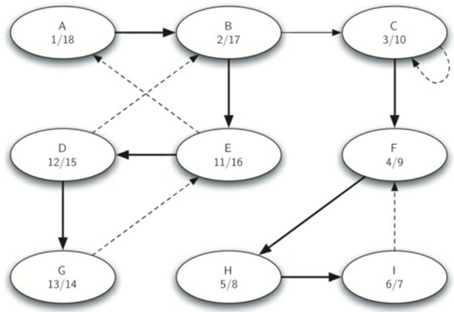
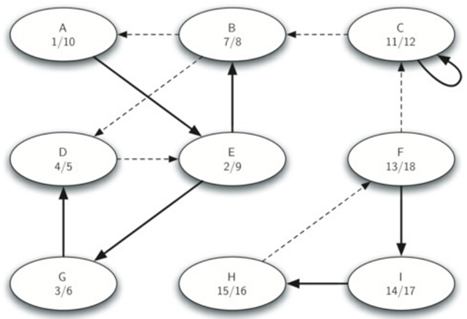
注意到，原始图在使用dfs后是一颗完整的树，转置图在使用dfs后变成了三个树。

\35. 最短路径问题，Dijkstra算法：
Dijkstra算法是一种迭代算法，用于计算从一个特定起始节点到图中所有其他节点的最短路径。

算法图解里的代码：



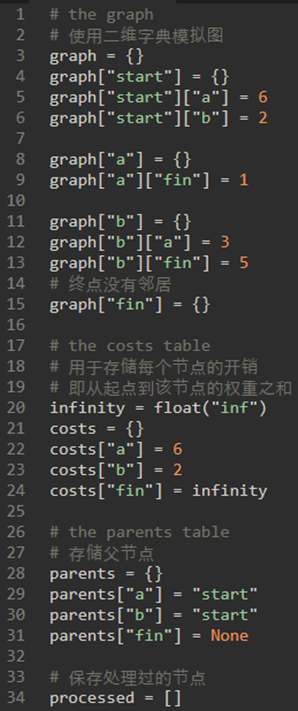
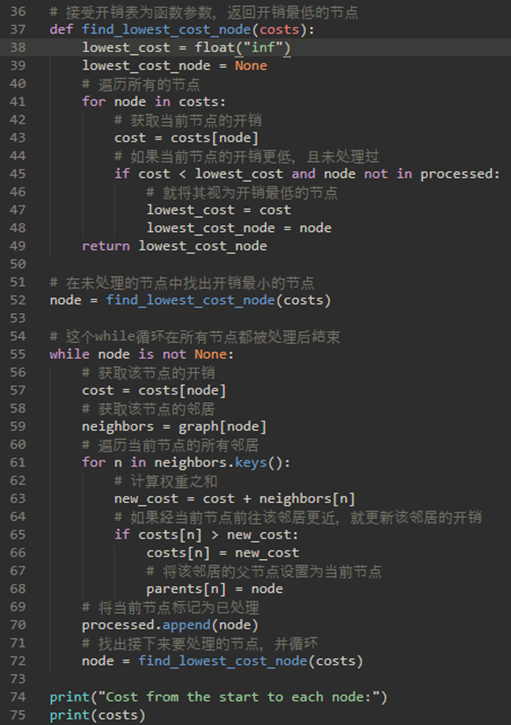
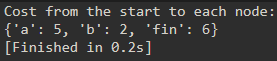
需要三个字典和一个数组：

a) 一个嵌套字典用于模拟图。

b) 一个字典用于存储每个节点的开销。

c) 一个字典用于存储每个节点的父节点。

d) 一个数组用于存储处理过的节点。

\36. 现在使用Graph类实现：
顶点类中的dist属性：跟踪从开始节点到每个目的地的总成本。
dist将包含从开始到所讨论的顶点的最小权重路径的当前总权重。

在上面代码中，我们使用无穷，这里我们只是将dist设置为一个大于任何真正的距离数字。

我们使用优先队列PriorityQueue，PriorityQueue类存储键值对的元组。值用于确定优先级，并且用于确定键在优先级队列中的位置。
在这个实现中，使用到顶点的距离作为优先级。

decreaseKey：
当一个已经在队列中的顶点的距离减小时，使用这个方法，将该顶点移动到队列的前面。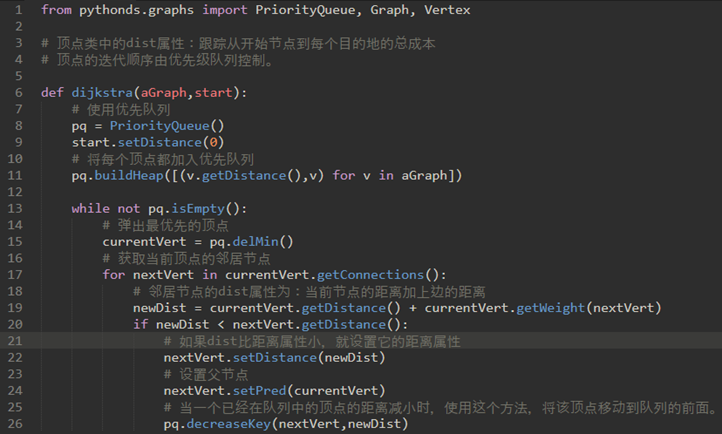

​ dist与distance属性的异同：
都是顶点到开始节点的距离。但是dist是最短距离，distance不一定是最短距离。

\37. Dijkstra算法分析：
构建优先级队列需要O(v)时间，因为我们最初将图中的每个顶点添加到优先级队列。

对于每个顶点执行一次while循环，因为顶点都在开始处添加，并且在那之后才被移除。在该循环中每次调用delMin，需要O(logV)时间。

组合循环和delMin，得出复杂度O(Vlog^V)。
for循环对于图中的每个边执行一次，并且在for循环中，对decreaseKey的调用需要时间O(Elog^V)。因此，组合运行时间为O((V+E)log^V)。

\38. Prim生成树算法：

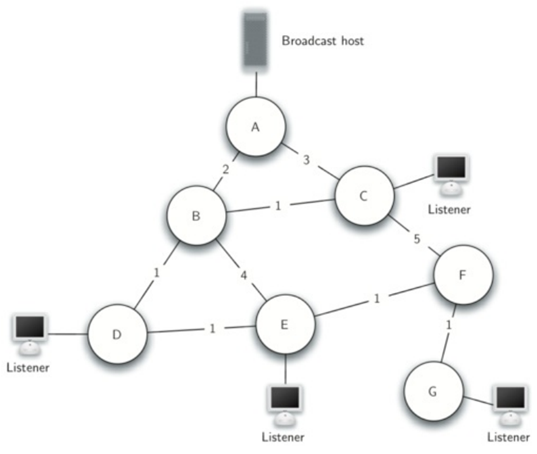
广播站想要让所有的Listener接收自己的消息，该如何做？

最简单的解决方案是广播站保存所有收听者的列表并向每个收听者发送单独的消息。

如果使用上面的做法，广播站将发送每个消息的四个副本。假设使用最小成本路径，让我们看看每个路由器处理同一消息的次数。
来自广播站的消息都通过路由器A，所以A看到每个消息的所有四个副本。路由器C只接收到其收听者每个消息的一个副本。然而，路由器B和D将收到每个消息的三个副本，因为路由器B和D在收听者1,2和3的最短路径上。当广播主机必须每秒发送数百条消息用于无线电广播，这是很多额外的流量。

还有一种方案是称为不受控泛洪策略。
洪水策略工作如下：
每个消息开始于将存活时间（ttl）值设置为大于或等于广播主机与其最远听者之间的边数量的某个数。每个路由器获得消息的副本，并将消息传递到其所有相邻路由器。当消息传递到ttl减少。每个路由器继续向其所有邻居发送消息的副本，直到ttl值达到0。不受控制的洪泛比我们的第一个策略产生更多的不必要的消息。

\39. 真正的解决方案是：建立最小权重生成树。
正式地定义如下：我们为图G=（V，E）定义最小生成树T如下。T是连接V中所有顶点的E的非循环子集。T中的边的权重的和被最小化。

\40. 生成树：
一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：
在连通网的所有生成树中，所有边的代价和最小的生成树（即权重和最小），称为最小生成树。（最小权重和生成树的简称）

说人话：最小生成树就是以最小的权重和连接所有的顶点的树。下面为38图的最小生成树。

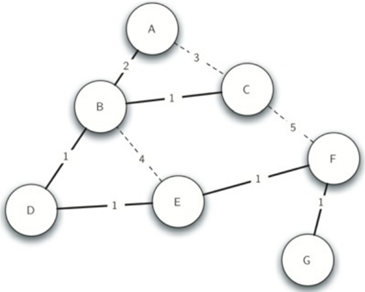
在这个例子中A将消息转发到B，B将消息转发到D和C。D将消息转发到E，E将它转发到F，F转发到G。没有路由器看到任何消息的多个副本，所有的收听者都会看到消息的副本。

\41. Prim算法是贪婪算法：
在每个步骤，我们将选择最小权重的下一步

prim算法的思路：

找到一个安全的边。我们定义一个安全边作为将生成树中的顶点连接到不在生成树中的顶点的任何边。这确保树将始终保持为树并且没有循环。

使用示意图如下：
从v1开始，在红线相交的线上找最小值。

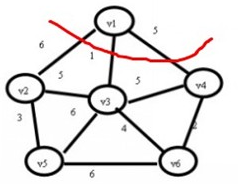
可以看到边v1-v3的权值最小为1，那么连接v1-v3。继续寻找，在与红线相交的边上查找最小值

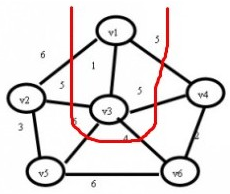
其他点同理：

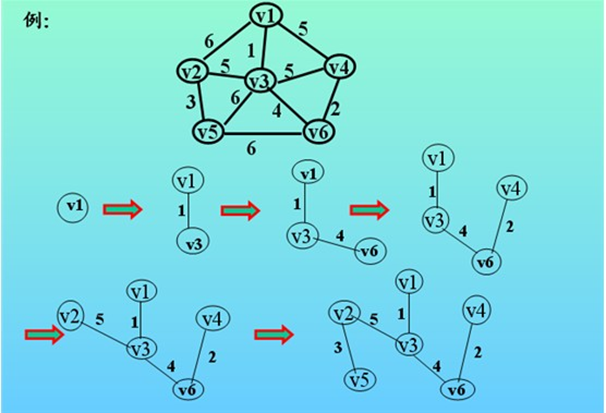
\42. 实现Prim算法的代码如下。
Prim算法类似于Dijkstra算法，它们都使用优先级队列来选择要添加到图中的下一个顶点。
思路：

a) 使用优先队列存储未连接的节点。

b) 寻找距离生成树最小路径的节点。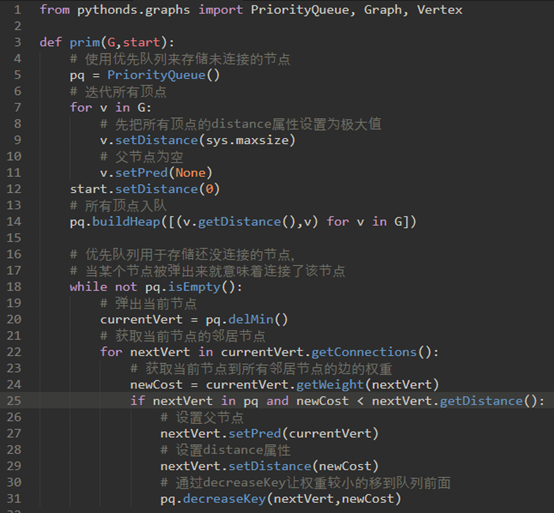

注意，当节点弹出来的时候才算连接了该节点。

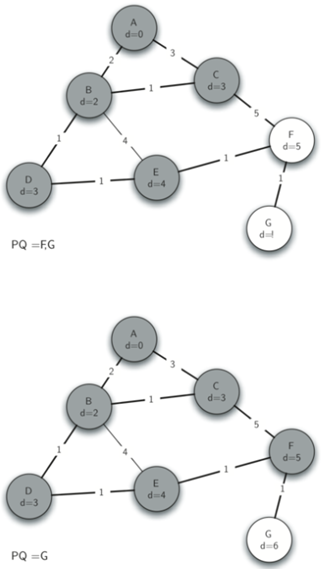
\43. 使用示意图：
从起始顶点A开始。到所有其他顶点的距离被初始化为无穷大。看看A的邻居，因为通过A到B和C的距离小于无限，更新另外两个顶点B和C的距离为2和3。这将B和C移动到优先级队列的前面。
通过将B和C的前导链接设置为指向A来更新前导链接。重要的是要注意，我们还没有正式向生成树添加B或C。在将节点从优先级队列中删除之前，不会将其视为生成树的一部分。

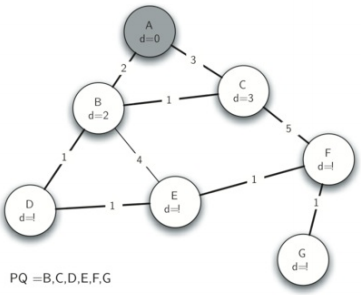
因为B有最小的距离，所以队列弹出B。
检查B的邻居，我们看到D和E可以更新。D和E都获得新的距离值，并更新它们的前导链接。

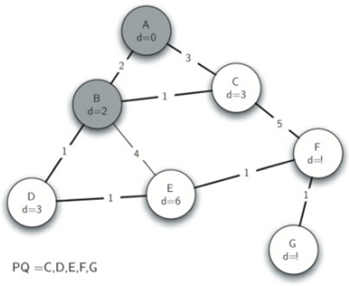
接着弹出C。C还在队列中的邻居节点是F，因此我们可以更新到F的距离，并调整优先级队列中的F的位置。

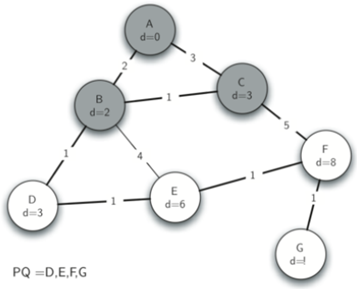
接着key最小的是D，现在我们检查与节点D相邻的顶点。我们发现可以更新E的distance属性（从6减小到4）。当我们这样做时，我们将E上的前趋链接改变为指向D，从而准备移植到生成树中不同的位置。算法的其余部分按照预期进行，将每个新节点添加到树中。

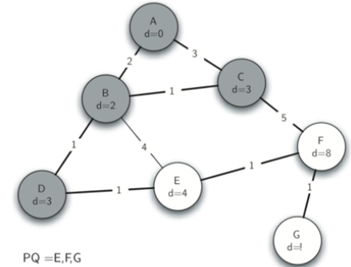
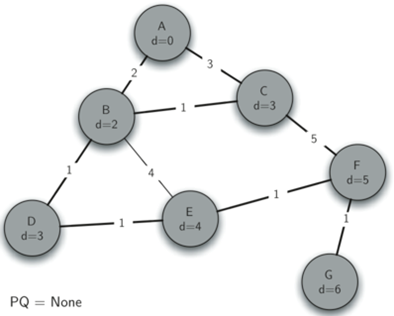
\44. 简单来说，prim算法就是：

a) 从图中选取一个节点作为起始节点（也是树的根节点），标记为已达；初始化所有未达节点到树的距离为到根节点的距离；

b) 从剩余未达节点中选取到树距离最短的节点i，标记为已达；更新未达节点到树的距离（如果节点到节点i的距离小于现距离，则更新）；

c) 重复步骤2直到所有n个节点均为已达。

\45. 示例二：

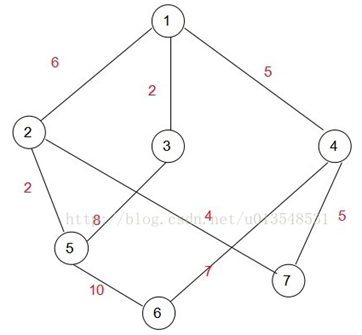
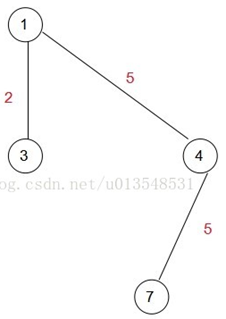
选择1为初始结点。遍历剩下的6个结点，找到距离生成树的最小那一个，显然是3，让3加入集合A，即intree[3]标记为1

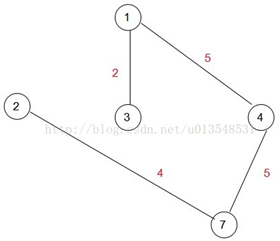
此时（1,5）=8（1,4）=5（1,2）=6，显然下一次应该加入A集合的是点4，所以：

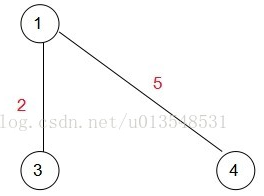
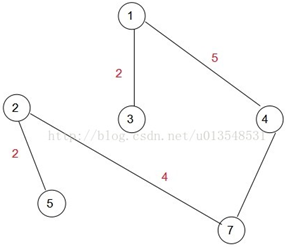
接下来就是：



fin