算法分析

\1. 大O符号：

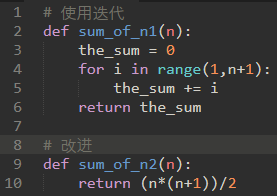
对执行语句进行计数，参数n通常称为‘问题的规模’，T(n)是解决问题大小为n所花费的时间。所以，第一个函数为T(n)=1+n。

数量级通常称为大O符号，写为O(f(n))。
它表示对计算中的实际步数的近似。函数f(n)提供了T(n)最主要部分的表示方法。
所以O(f(n))=O(n)。
常用函数阶图：


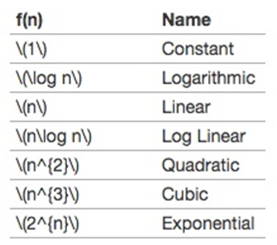
上面代码的复杂度为O(n^2)。理由：
分配操作数分为四个项的总和:

a) 第一个项是常数3，表示片段开始的三个赋值语句。

b) 第二项是3n^2,因为由于嵌套迭代，有三个语句执行n^2次。

c) 第三项是2n,两个语句迭代n次。

d) 第四项是常数1，表示最终赋值语句。

得出T(n)=3+3n^2+2n+1=3n^2+2n+4

\2. 乱序字符串是指一个字符串只是另一个字符串的重新排列。例如，’heart’和’earth’就是乱序字符串。我们假设所讨论的两个字符串具有相等的长度，并且他们由26个小写字母集合组成。

我们的目标是写一个布尔函数，它将两个字符串做参数并检验它们是不是乱序。
解法1：检查。复杂度为O(n^2)

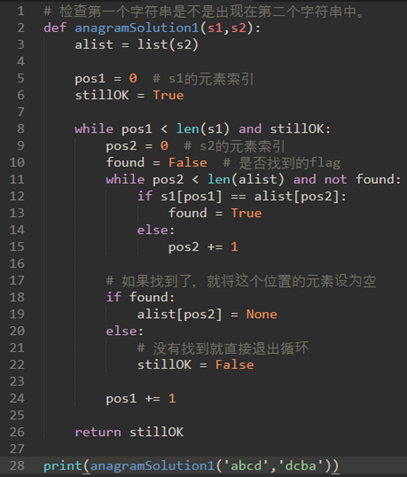
解法2:排序和比较。

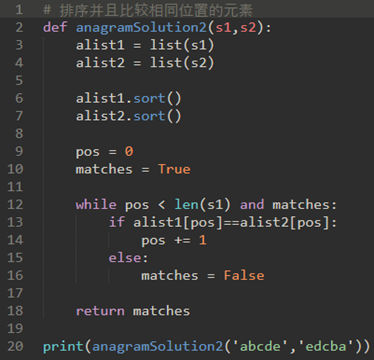
排序复杂度通常是O(n^2)或O(nlogn)。所以排序操作比迭代花费更多。
解法3：穷举法。复杂度O(n!)
解决这类问题的强力方法是穷举所有可能性。
对于乱序检测，我们可以生成s1的所有乱序字符串列表，然后查看是不是有s2。

当s1生成所有可能的字符串时，第一个位置有n种可能，第二个位置有n-1种，第三个位置有n-3种。总数为n∗(n−1)∗(n−2)∗…∗3∗2∗1n∗(n−1)∗(n−2)∗…∗3∗2∗1，即n!。虽然一些字符串可能是重复的，程序也不可能提前知道这样，所以他仍然会生成n!个字符串。

解法4:计数和比较。复杂度为O(n)。
两个乱序字符串具有相同数目的a,b,c等字符。我们首先计算的是每个字母出现的次数。由于有26个可能的字符，我们就用一个长度为26的列表，每个可能的字符占一个位置。每次看到一个特定的字符，就增加该位置的计数器。最后如果两个列表的计数器一样，则字符串为乱序字符串

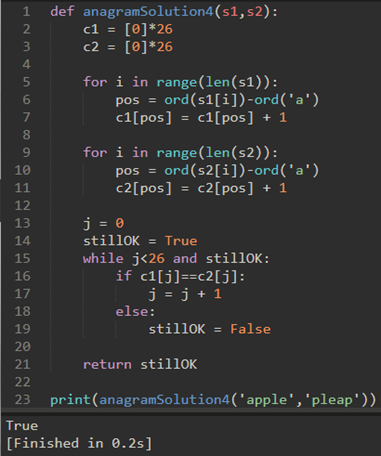
表示s1[i]为第几个字母
虽然最后一个方案在线性时间执行，但它需要额外的存储来保存两个字符计数列表。换句话说，该算法牺牲了空间以获得时间。

自己思路：

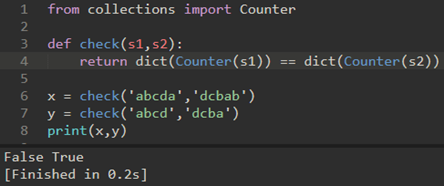
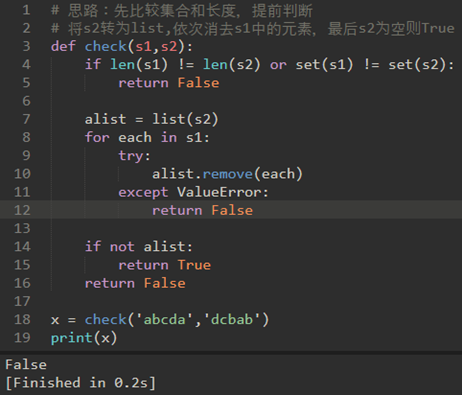
\3. 列表两个常见的操作是索引和分配到索引位置。
无论列表有多大，索引和分配索引都需要相同的时间。当这样的操作和列表的大小无关时，它们是O（1）。

拼接运算符为O(k)。k是要拼接的列表的大小。

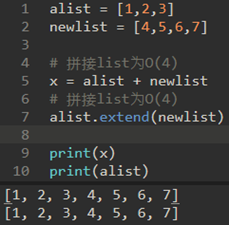
\4. 看一下下面四种构造list的方法

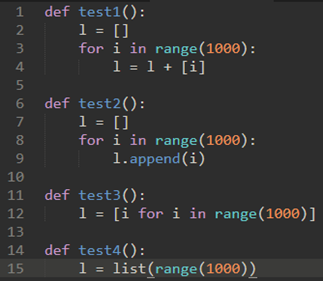
我们使用time模块测试：

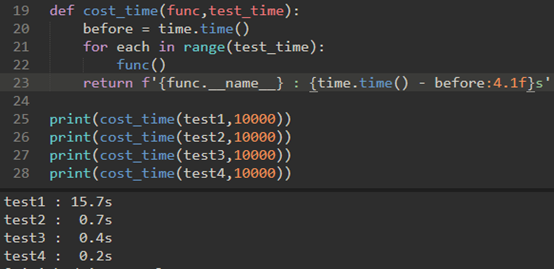
但是，可以使用更好的timeit模块：
timeit模块旨在允许Python开发人员通过在一致的环境中运行函数并使用尽可能相似的操作系统的时序机制来进行跨平台时序测量。

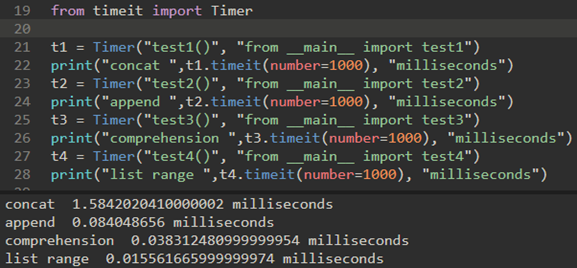
使用timeit，你需要创建一个Timer对象，其参数是两个语句，两个参数都是字符串格式：

a) 第一参数是你想要执行时间的Python语句

b) 第二参数是将运行一次以设置测试的语句

简单来说就是：
第一个是要执行的代码对象，
第二个是导入被执行的对象。

from main import test1从__main__命名空间导入到timeit设置的命名空间中。
timeit这么做是因为它想在一个干净的环境中做测试，而不会因为可能有你创建的任何杂变量，以一种不可预见的方式干扰你函数的性能。

默认情况下，timeit将尝试运行语句一百万次。，它返回时间作为表示总秒数的浮点值。

\5. 为什么pop()是O(1)，而pop(n)是O(n)？

很简单，因为pop操作都是O(1)，但是pop(n)之后需要将后面list的元素连接上去。
也就是说：当一个项从列表前面取出，列表中的其他元素靠近起始位置移动一个位置。

证明pop(0)是O(n),pop()是O(1)。

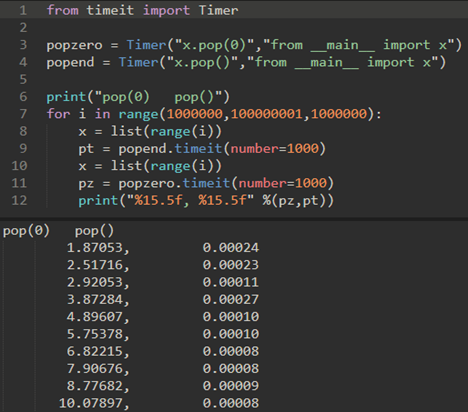
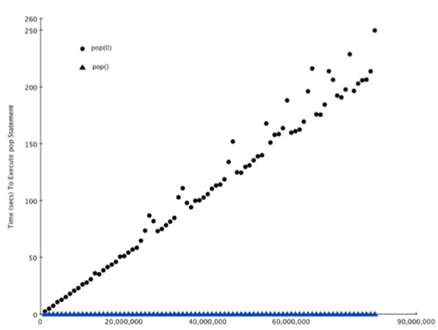
这也能解释为什么insert也是O(n)：
在插入元素之后，该元素后面的元素都需要移动一个位置。
del slice,set slice同理，在删除/设置切片之后，都需要移动元素位置。

\6. 字典的大O：

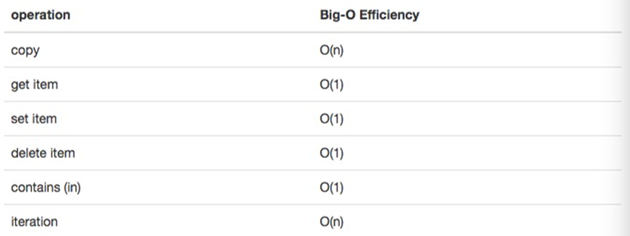
需要注意的是，字典的contains操作也是O(1)。

\7. 证明列表的contains操作符是O(n)，字典的contains操作符是O(1)。

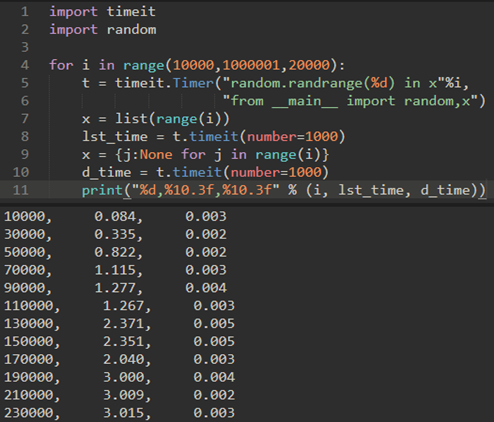
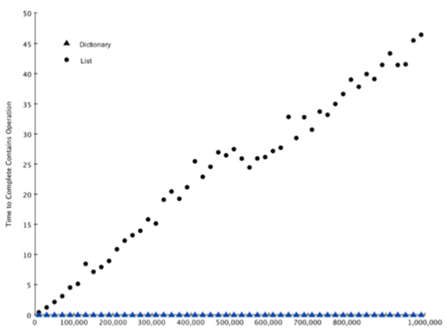
基本数据结构

\8. 什么是数据线性结构：
我们从四个简单但重要的概念开始研究数据结构。栈，队列，deques(双向队列),列表是一类数据的容器，它们数据项之间的顺序由添加或删除的顺序决定。一旦一个数据项被添加，它相对于前后元素一直保持该位置不变。诸如此类的数据结构被称为线性数据结构。

\9. 线性数据结构有两端，有时被称为左右，某些情况被称为前后。也可以称为顶部和底部。

将两个线性数据结构区分开的方法是添加和移除项的方式，特别是添加和移除项的位置。
例如一些结构允许从一端添加项，另一些允许从另一端移除项。

\10. 什么是栈：
栈（有时称为“后进先出栈”）中添加移除新项总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。
添加/移除新项为顶部。

栈之所以重要是因为它能反转项的顺序。插入跟删除顺序相反。
例如，每个web浏览器都有一个返回按钮。当你浏览网页时，这些网页被放置在一个栈中（实际是网页的网址）。你现在查看的网页在顶部，你第一个查看的网页在底部。如果按‘返回’按钮，将按相反的顺序浏览刚才的页面。

\11. 栈的抽象数据类型：
栈被构造为项的有序集合，其中项被添加和从末端移除的位置称为“顶部”。栈是有序的LIFO。栈操作如下。

a) Stack()创建一个空的新栈。它不需要参数，并返回一个空栈。

b) push(item)将一个新项添加到栈的顶部。它需要item做参数并不返回任何内容。

c) pop()从栈中删除顶部项。它不需要参数并返回item。栈被修改。

d) peek()从栈返回顶部项，但不会删除它。不需要参数。不修改栈。

e) isEmpty()测试栈是否为空。不需要参数，并返回布尔值。

f) size()返回栈中的item数量。不需要参数，并返回一个整数。

\12. s是已经创建的空栈，下图展示了栈操作序列的结果。栈中，顶部项列在最右边。

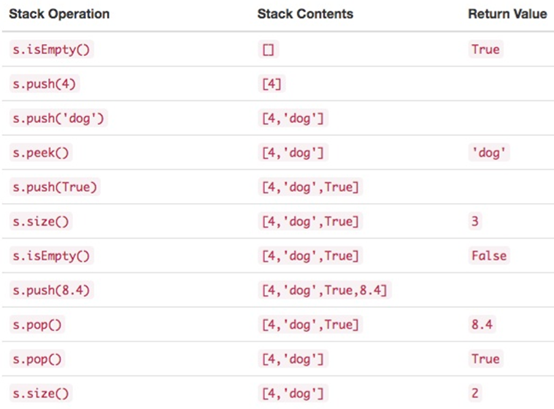
\13. Python实现栈：
在Python中，与任何面向对象编程语言一样，抽象数据类型（如栈）的选择的实现是创建一个新类。栈操作实现为类的方法。
回想一下，Python中的列表类提供了有序集合机制和一组方法。
例如，如果我们有列表[2,5,3,6,7,4]，我们只需要确定列表的哪一端将被认为是栈的顶部。一旦确定，可以使用诸如append和pop的列表方法来实现操作。
所以，我们使用list尾部作为stack顶部：

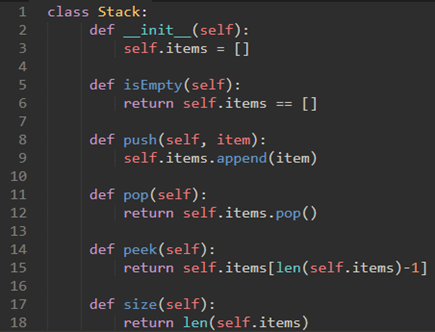
题外话：
list源码中有一个ob_size变量，ob_size变量存储的就是对象的长度,所以每次调用_len_()方法的时候,返回的是一个已经存储好了的变量,并没有对列表进行遍历操作,所以_len_()时间复杂度是O(1)。而in需要遍历，所以list的in是O(n)。

\14. 当然，其实这些基础数据结构都是不用自己定义的，可以直接使用pythonds模块：
（ds:Data Structures）

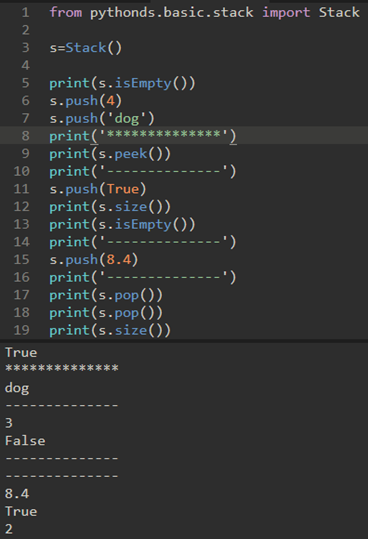
\15. 简单括号匹配:
编写一个算法，能够从左到右读取一串符号，并决定符号是否平衡。(简单来说就是判断左右括号能否组成一个完整的括号)

我们观察到：处理的第一个开始符号必须等待直到其匹配最后一个符号。结束符号以相反的顺序匹配开始符号。他们从内到外匹配。这是一个可以用栈解决问题的线索。


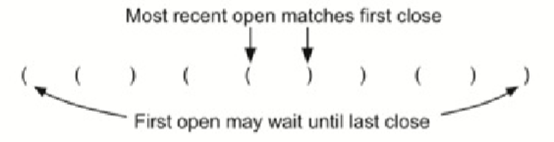
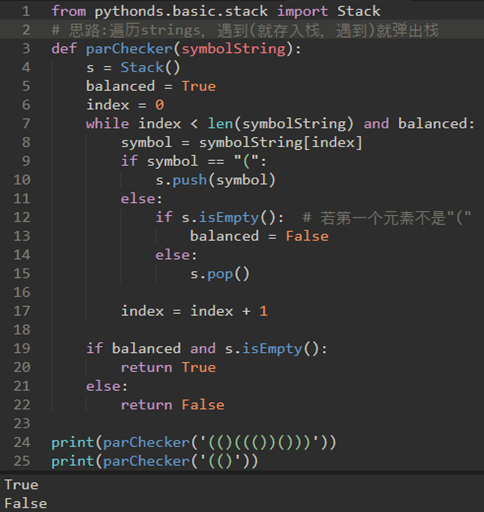
主要思路:遍历string，遇到（就存入栈，遇到）就弹出，最后如果栈是空则匹配成功。
从空栈开始，从左到右处理括号字符串。如果一个符号是一个（，将其作为一个信号，对应的）稍后会出现。

注：我之前的想法是：先将string存入栈，然后复制一份反转的string挨个存入栈，之后不断弹出，如果不匹配则失败。
这种思想是很傻逼的，尽量使用一个栈就行了。

\16. 符号匹配：前面是匹配圆括号，现在要匹配包括小括号、中括号、大括号混在一起的字符串。

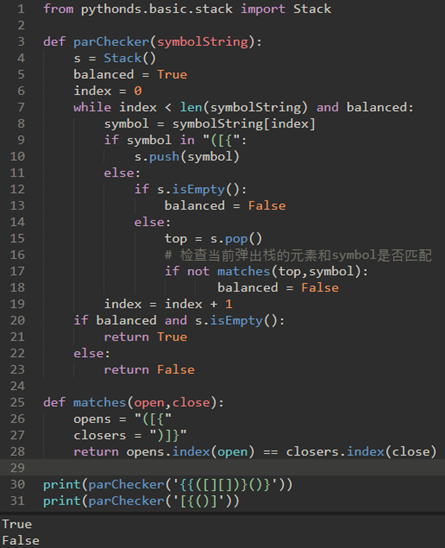
上面的matches函数，称之为辅助函数匹配。用于检查栈中每个删除的符号，以查看它是否与当前结束符号匹配。
注意，这里不需要使用三个栈，只要在弹出的时候进行检查就可以了。使用一个栈就行了。

\17. 十进制转换成二进制：

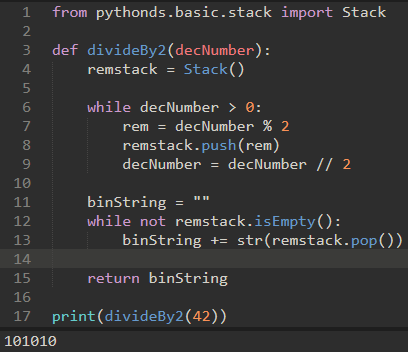
我一开始的思路是：

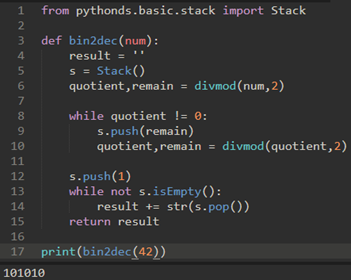
上面的代码很蠢，注意要使用函数的参数作为while的判断。
修改了一下变成：

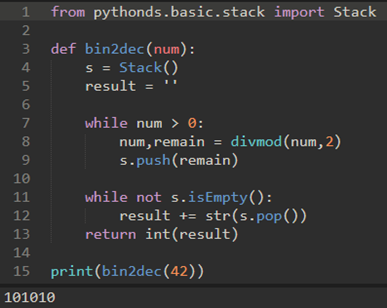
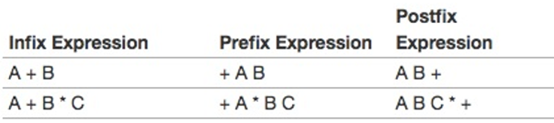
\18. 中缀前缀和后缀表达式：
像BC这样的表达式中的号称为中缀。因为*运算符在它处理的两个操作数之间。

改变操作符的位置得到了两种新的表达式格式，前缀和后缀：
中缀表达式A+B,如果我们移动两个操作数之间的运算符会发生什么？结果表达式变成+AB。同样，我们也可以将运算符移动到结尾，得到AB+

前缀表达式符号要求所有运算符在它们处理的两个操作数之前。
后缀要求其操作符在相应的操作数之后。


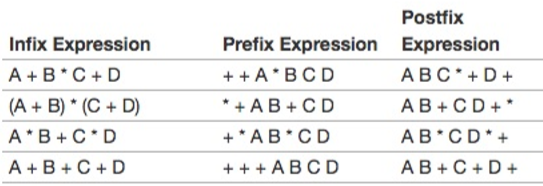
总结：前缀/后缀的算法都很简单，先加括号，后移动符号。
如a+b*c+d:

a) 添加括号变成((a+(b*c))+d)

b) 第一次移动符号变成((a+bc*)+d)

c) 第二次移动符号变成(abc*+)+d

d) 第三次移动符号变成abc*+d+

同理：(A+B)C-(D-E)(F+G)变成：
-+abc-de+fg或ab+cde-fg+-

\19. 中缀转后缀通用法：
先找规律：A+BC变成ABC+

a) A，B和C保持在它们的相对位置。

b) 因为*优先级高于+，原始表达式中的运算符的顺序在生成的后缀表达式中相反。

c) 当我们处理表达式时，操作符必须保存在某处，因为它们相应的右操作数还没有看到。

(A+B)C变成AB+C
当我们看到左括号时，保存它，表示高优先级的另一个运算符将出现。该操作符需要等到相应的右括号出现以表示其位置。当右括号出现时，可以从栈中弹出操作符。

\20. 所以，整体思路为：

a) 创建一个名为opstack的空栈以保存运算符。给输出创建一个空列表。

b) 通过使用字符串方法拆分将输入的中缀字符串转换为标记列表。

c) 从左到右扫描标记列表。

\1. 如果标记是操作数，将其附加到输出列表的末尾。

\2. 如果标记是左括号，将其压到opstack上。

\3. 如果标记是右括号，则弹出opstack，直到删除相应的左括号。将每个运算符附加到输出列表的末尾。

\4. 如果标记是运算符，*，/，+或-，将其压入opstack。但是，首先删除已经在opstack中具有更高或相等优先级的任何运算符，并将它们加到输出列表中。

d) 当输入表达式被完全处理时，检查opstack。仍然在栈上的任何运算符都可以删除并加到输出列表的末尾。

\21. 简单来说就是:从左往右字符串

a) 1.遇到操作数，存到list里；

b) 2.遇到运算符，入栈；

c) 3.遇到左括号，将其入栈；

d) 4.遇到右括号，执行出栈操作，弹出元素，直到弹出的是左括号，左括号不输出；

e) 5.遇到其他运算符+-*/时，弹出所有优先级大于或等于该运算符的栈顶元素，然后将该运算符入栈；

f) 6.最终将栈中的元素依次出栈，输出。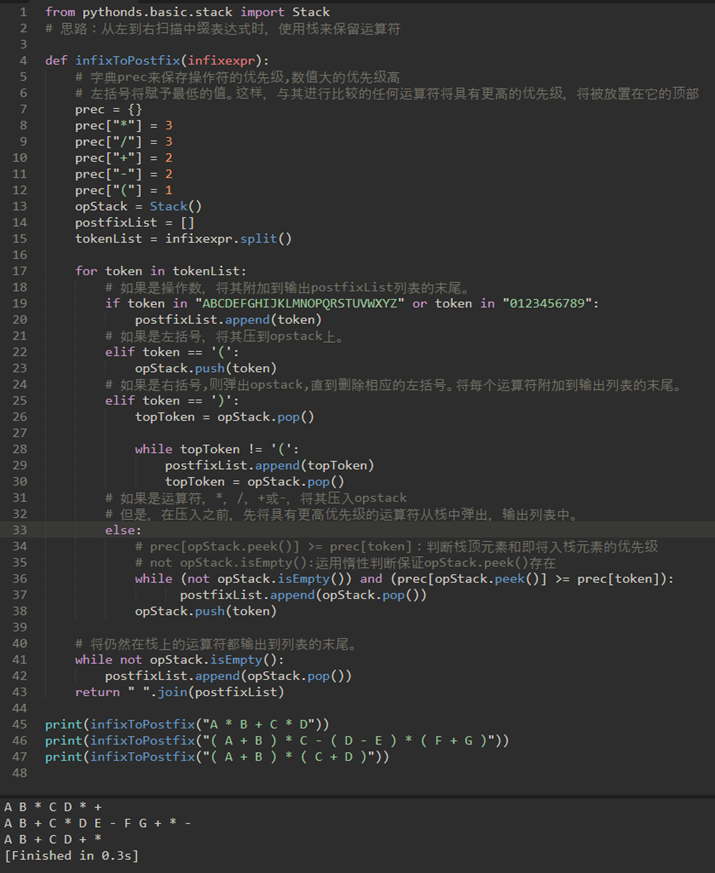

根据上面说述：
注意36行是 >=，不是>

\22. 后缀表达式求值:
在扫描后缀表达式时，它必须等待操作数，而不像上面的转换算法中的运算符。解决问题的另一种方法是，每当在输入上看到运算符时，计算两个最近的操作数。

后缀表达式456*+:
首先遇到操作数4和5，此时，你还不确定如何处理它们，直到看到下一个符号。将它们放置到栈上，确保它们在下一个操作符出现时可用。
后缀表达式78+32+/:
栈的大小增长收缩，然后再 子表达式求值的时候再次增长。

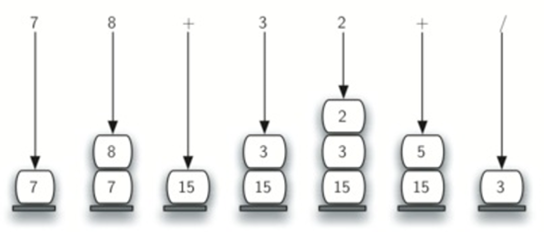
总结算法：

a) 1.创建一个名为operandStack的空栈。

b) 2.拆分字符串转换为标记列表。

c) 3.从左到右扫描标记列表。

\1. 如果标记是操作数，将其从字符串转换为整数，并将值压到operandStack。

\2. 如果标记是运算符*/+-，它将需要两个操作数，弹出operandStack两次。第一个弹出的是第二个操作数，第二个弹出的是第一个操作数。执行算术运算后，将结果压到操作数栈中。

d) 4.当输入的表达式被完全处理后，结果就在栈上，弹出operandStack并返回值。

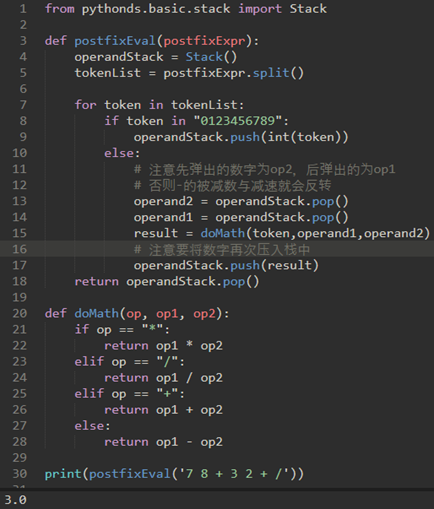
注意：当用于除法的操作符从栈中弹出时，它们被反转。所以先弹出的数字为op2，后弹出的数字为op1。

\23. 什么是队列：
队列是项的有序结合，其中添加新项的一端称为队尾，移除项的一端称为队首。（先进先出）
当一个元素从队尾进入队列时，一直向队首移动，直到它成为下一个需要移除的元素为止。

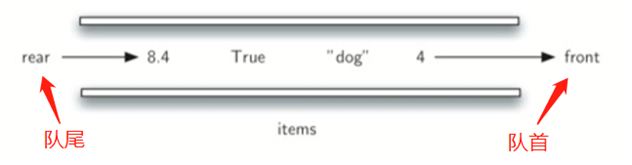
这种排序称为FIFO。

\24. 队列抽象数据类型：

a) Queue()创建一个空的新队列。它不需要参数，并返回一个空队列。

b) enqueue(item)将新项添加到队尾。它需要item作为参数，并不返回任何内容。

c) dequeue()从队首移除项。它不需要参数并返回item。队列被修改。

d) isEmpty()查看队列是否为空。它不需要参数，并返回布尔值。

e) size()返回队列中的项数。它不需要参数，并返回一个整数。

和stack相比，少了一个peek（窥视栈顶元素）
右边表示队首。4是第一个入队的项，因此它dequeue返回的第一个项。

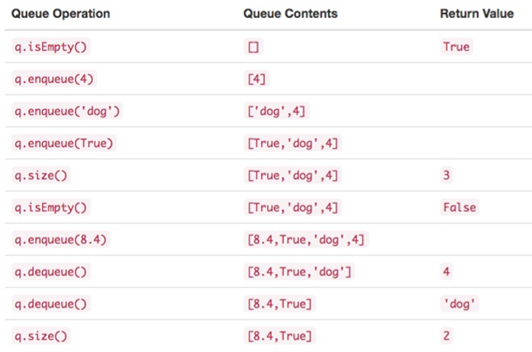
\25. Python实现队列：

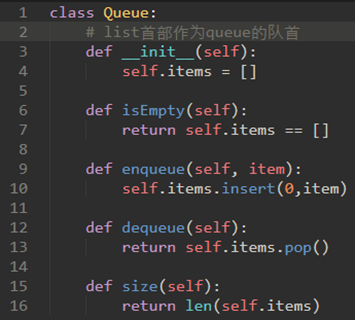
\26. 模拟：烫手山芋：
烫手山芋游戏，在这个游戏中，孩子们围成一个圈，并尽可能快的将一个山芋递给旁边的孩子。在某一个时间，动作结束，有山芋的孩子从圈中移除。游戏继续开始直到剩下最后一个孩子。

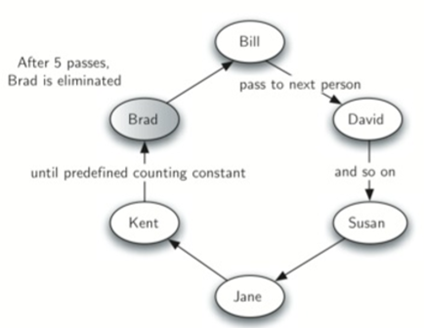
这个游戏相当于著名的约瑟夫问题。
故事讲的是，他和他的39个战友被罗马军队包围在洞中。他们决定宁愿死，也不成为罗马人的奴隶。他们围成一个圈，其中一人被指定为第一个人，顺时针报数到第七人，就将他杀死。约瑟夫斯是一个成功的数学家，他立即想出了应该坐到哪才能成为最后一人。最后，他加入了罗马的一方，而不是杀了自己。

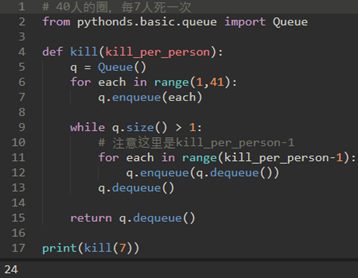
\27. 对于这个问题，我们转化为下面描述：
学生排成一列，列首的学生上去摸一下山芋，摸完就返回队列尾部，第7个摸山芋的人被踢出队伍。

在这里，小明出队列后又进入队列，但是只要是8的倍数的都会被踢出队伍。
那么我们只要把前六个踢出后又加入队伍，但第八个不加入队伍即可，直到队列大小为1。

假设拿着山芋的孩子在队列的前面。当拿到山芋的时候，这个孩子将先出列再入队列，把他放在队列的最后。经过num次的出队入队后，前面的孩子将被永久移除队列。并且另一个周期开始，继续此过程，直到只剩下一个名字（队列的大小为1）。


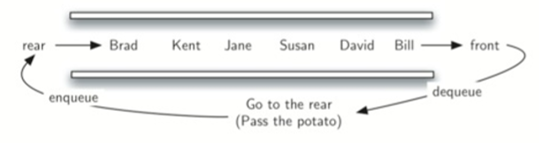
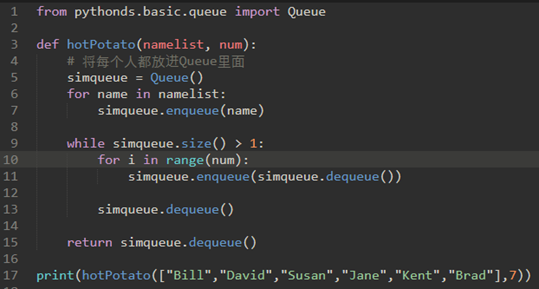
10、11行代码就是：首先循环7个人，这7个人出队后又进队。
然后第8个人直接出队，不再进队。（13行）

所以约瑟夫问题的求解为：

\28. 模拟打印机：
当学生向共享打印机发送打印任务时，任务被放置在队列中以便以先来先服务的方式被处理。
有10个学生在任意时间来打印室打印，每个学生打印2次，每次1-20页。打印机低质量打印10页/min,高质量打印5页/min。打印机应该用高质量还是低质量，以此来减少学生等待时间？

\29. 思路：

a) 新建一个打印任务的队列，当打印机完成任务时，它将检查队列，以检查是否有剩余的任务要处理。

b) 我们感兴趣的是学生等待打印的平均时间。这等于任务在队列中等待的平均时间量。

c) 通过使用1和20之间的随机数来模拟打印任务的实际长度。

d) 若实验室中有10个学生，每人打印两次，则平均每小时有20个打印任务。意味着平均每180秒将有一个任务。

e) 对于每一秒，我们可以通过生成1到180之间的随机数来模拟打印任务发生的机会。如果数字是180，我们说一个任务已经创建。

\30. 主要模拟步骤：

a) 创建打印任务的队列，每个任务都有个时间戳。队列启动的时候为空。

b) 每秒（currentSecond）：

\1. 是否创建新的打印任务？如果是，将currentSecond作为时间戳添加到队列

\2. 如果打印机不忙并且有任务在等待：

a) 从打印机队列中弹出任务给打印机

b) 从currentSecond中减去时间戳，以计算该任务的等待时间。

c) 将该任务的等待时间附件到列表中稍后处理。

d) 根据打印任务的页数，确定需要多少时间。

\3. 打印机需要一秒打印，所以得从该任务的所需的等待时间减去一秒。

\4. 如果任务已经完成，换句话说，所需的时间已经达到零，打印机空闲。

c) 模拟完成后，从生成的等待时间列表中计算平均等待时间。

\31. Python实现:
为了设计此模拟，我们将为上述三个真实世界对象创建类：Printer,Task,PrintQueue

\32. 是在没有搞懂，先跳过吧。（55到59页）

\33.

\34.

\35.

\36. 什么是Deque：
deque（也称为双端队列）是与队列类似的项的有序集合。它有两个端部，首部和尾部，并且项在集合中保持不变。
deque不同的地方是可以在前面或后面添加新项。同样，可以从任一端移除现有项。
在某种意义上，这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。

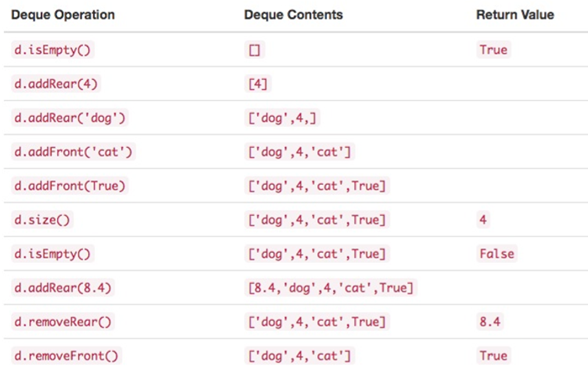
\37. Deque抽象数据类型：

a) Deque()创建一个空的新deque。它不需要参数，并返回空的deque。

b) addFront(item)将一个新项添加到deque的首部。它需要item参数并不返回任何内容。

c) addRear(item)将一个新项添加到deque的尾部。它需要item参数并不返回任何内容。

d) removeFront()从deque中删除首项。它不需要参数并返回item。deque被修改。

e) removeRear()从deque中删除尾项。它不需要参数并返回item。deque被修改。

f) isEmpty()测试deque是否为空。它不需要参数，并返回布尔值。

g) size()返回deque中的项数。它不需要参数，并返回一个整数。

首部的内容列在右边：

\38. Python实现Deque：
还是使用list：列表的尾部为Deque的首部。

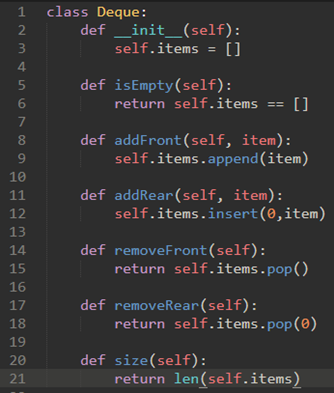
在这个实现中，从前面添加和删除项是O(1)，而从后面添加和删除是O(n)。
考虑到添加和删除项是出现的常见操作。重要的是要确定我们知道在实现中前后都分配在哪里。

但是真正的deque头部或尾部的增加删除操作的复杂度都是固定的。

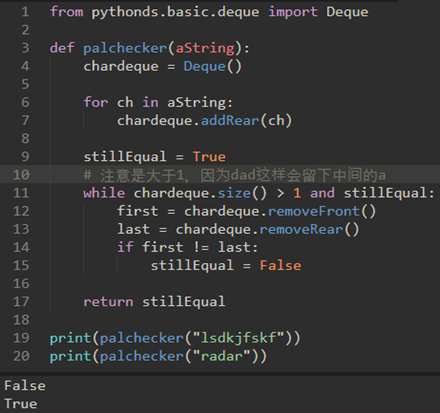
\39. 回文检查：
使用deque来存储字符串的字符。
从左到右处理字符串，并将每个字符添加到deque的尾部。在这一点上，deque像一个普通的队列。
利用deque的双重功能。deque的首部保存字符串的第一个字符，deque的尾部保存最后一个字符。
直接弹出并比较首尾字符，只有当它们匹配时才继续。如果可以持续匹配首尾字符，我们最终要么用完字符，要么留出大小为1的deque，取决于原始字符串的长度是偶数还是奇数。

\40. 列表：
列表是项的集合，其中每个项保持相对于其他项的相对位置。

\41. 无序列表抽象数据类型:

a) List()创建一个新的空列表。它不需要参数，并返回一个空列表。

b) add(item)向列表中添加一个新项。它需要item作为参数，并不返回任何内容。假定该item不在列表中。

c) remove(item)从列表中删除该项。它需要item作为参数并修改列表。假设项存在于列表中。

d) search(item)搜索列表中的项目。它需要item作为参数，并返回一个布尔值。

e) isEmpty()检查列表是否为空。它不需要参数，并返回布尔值。

f) size（）返回列表中的项数。它不需要参数，并返回一个整数。

g) append(item)将一个新项添加到列表的末尾，使其成为集合中的最后一项。它需要item作为参数，并不返回任何内容。假定该项不在列表中。

h) index(item)返回项在列表中的位置。它需要item作为参数并返回索引。假定该项在列表中。

i) insert(pos，item)在位置pos处向列表中添加一个新项。它需要item作为参数并不返回任何内容。假设该项不在列表中，并且有足够的现有项使其有pos的位置。

j) pop()删除并返回列表中的最后一个项。假设该列表至少有一个项。

k) pop(pos)删除并返回位置pos处的项。它需要pos作为参数并返回项。假定该项在列表中。

\42. 实现无序列表：链表
我们需要确保我们可以保持项的相对定位。然而，没有要求我们维持在连续存储器中的定位。

对于上面的值，可以通过简单地从一个项 到下一个项的链接来表示。

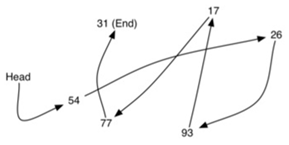
Node类:
链表实现的基本构造块是节点。
每个节点对象必须至少保存两个信息。

a) 节点必须包含列表项本身。我们将这个称为节点的数据字段。

b) 每个节点必须保存对下一个节点的引用。

\43. Node类的Python实现：
构造一个节点，需要提供该节点的初始数据值。
Node类还包括访问，修改数据和访问下一个引用的常用方法。

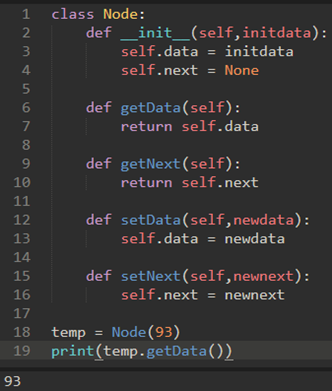
Python引用值None将在Node类和链表本身发挥重要作用。引用None代表没有下一个节点。请注意在构造函数中，最初创建的节点next被设置为None。有时这被称为接地节点，因此我们使用标准接地符号表示对None的引用。将None显式的分配给初始下一个引用值是个好主意。

\44. Unordered List类(无序列表类):
无序列表将从一组节点构建，每个节点通过显式引用链接到下一个节点。
只要我们知道在哪里找到第一个节点（包含第一个项），之后的每个项可以通过连续跟随下一个链接找到。
考虑到这一点，UnorderedList类必须保持对第一个节点的引用。

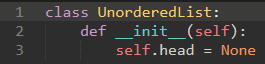
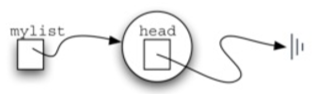
每个链表对象将维护对链表头部的单个引用。

\45. 链表的头指代列表的第一项的第一节点,该节点保存对下一个节点（下一个项）的引用。
重要的是注意链表类本身不包含任何节点对象。
它只包含对链接结构中第一个节点的单个引用。

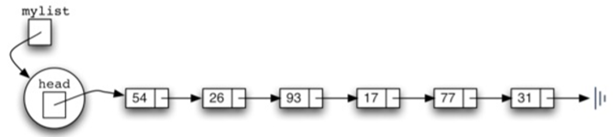
\46. 如果需要还可以为Unordered List类添加一个isEmpty方法来判断链表是否为空。

\47. 现在设计一个类似于栈的链表(最后添加的节点作为链表的头结点)
也就是说，当执行完:

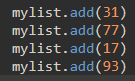
链表变成：


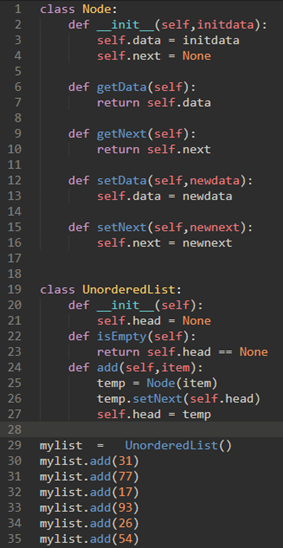
注意26行和27行的顺序绝对不能颠倒：
下面演示了26行和27行的执行顺序：

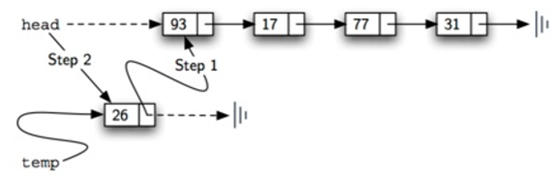
\48. 既然链表已经定义完毕，那么需要定义遍历链表的方法了：size，search，remove
他们的执行示意图如下：


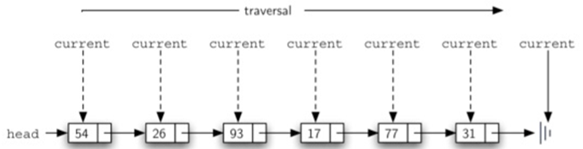
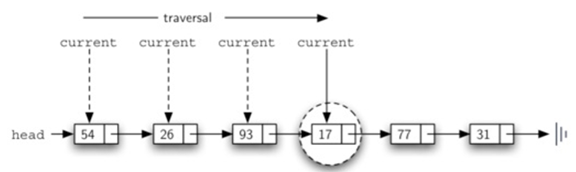
remove分两种：



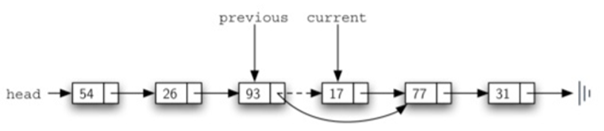
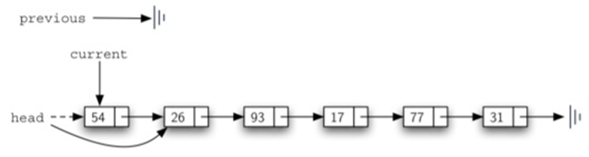
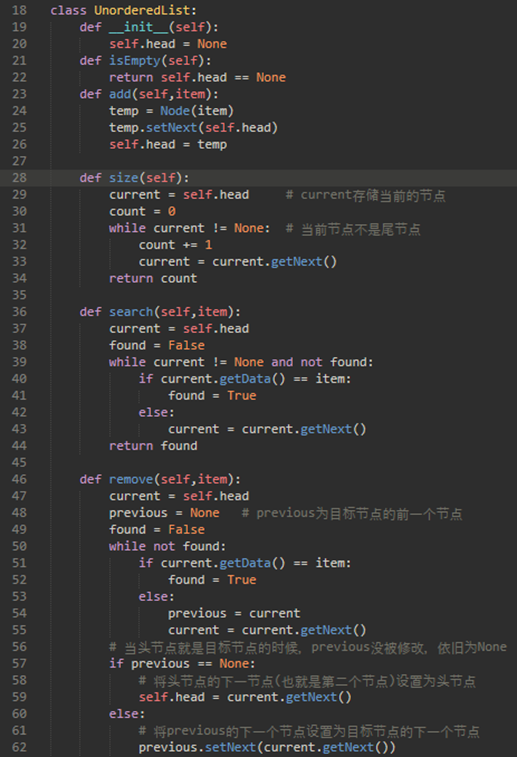
这里需要注意54行和55行：
previous必须先将一个节点移动到current的位置，才可以移动current。
也就是说，previous必须赶上current，然后current才能前进。
这个过程通常被称为“英寸蠕动”

注意上面的remove方法当查找不到的时候就会报错，可以加一层判断：

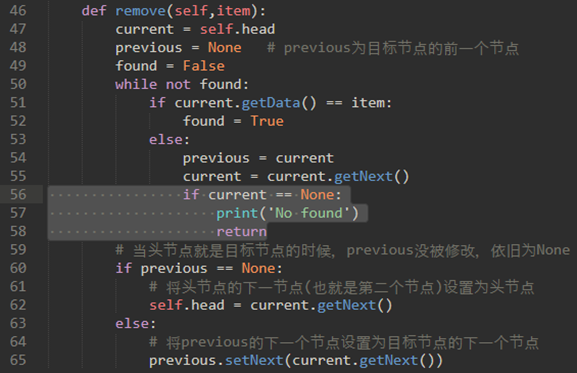
\49. 有序列表抽象数据结构:
类似于python里排序完毕的list，不过有序列表是一个链表

有序列表的结构是项的集合，其中每个项保存基于项的一些潜在特性的相对位置。排序通常是升序或降序，并且我们假设列表项具有已经定义的有意义的比较运算。许多有序列表操作与无序列表的操作相同。

a) OrderedList()创建一个新的空列表。它不需要参数，并返回一个空列表。

b) add(item)向列表中添加一个新项。它需要item作为参数，并不返回任何内容。假定该item不在列表中。

c) remove(item)从列表中删除该项。它需要item作为参数并修改列表。假设项存在于列表中。

d) search(item)搜索列表中的项目。它需要item作为参数，并返回一个布尔值。

e) isEmpty()检查列表是否为空。它不需要参数，并返回布尔值。

f) size（）返回列表中的项数。它不需要参数，并返回一个整数。

g) index(item)返回项在列表中的位置。它需要item作为参数并返回索引。假定该项在列表中。

h) pop()删除并返回列表中的最后一个项。假设该列表至少有一个项。

i) pop(pos)删除并返回位置pos处的项。它需要pos作为参数并返回项。假定该项在列表中

\50. 实现有序列表，isEmpty，search，add和无序列表一样，因为这三个方法与节点的实际项值无关。需要修改的是add和search方法。

这很好理解，假如我们查找60是否在链表里，当我们查找到77时，发现77>60，所以可以尽快结束查找，直接return False


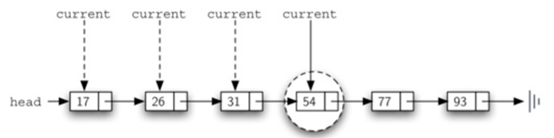
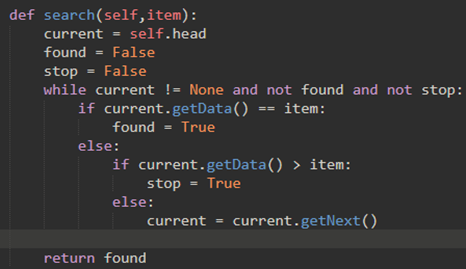
add也很好理解：首先找到需要插入位置的前后两个节点，然后插入即可。

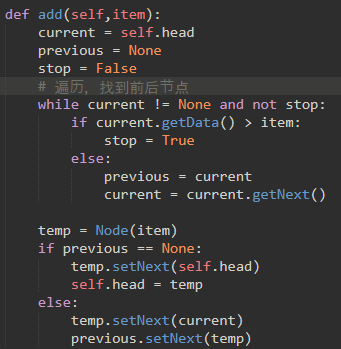
\51. 注意到此实现的性能与早前针对Python列表给出的实际性能不同。
这表明链表不是Python列表的实现方式。Python列表的实际实现基于数组的概念。

链表实现保持逻辑顺序，而不需要物理存储要求。

解释一下47的链表要设计成类似于栈的链表(最后添加的节点作为链表的头结点)
因为这样的话，使用add方法永远都是在链表头部，复杂度为O(1)，如果新节点是接在尾节点上，那么需要遍历到最后的节点，复杂度为O(n)

递归

\52. 递归：
递归是一种解决问题的方法，将问题分解为更小的子问题，直到得到一个足够小的问题可以被很简单的解决。
通常递归涉及函数调用自身。递归允许我们编写优雅的解决方案，解决可能很难编程的问题。

\53. 使用递归的思路：

a) 基线条件是什么（什么时候结束递归）。

b) 每一步递归都要缩小问题的规模。
(递归算法必须改变其状态并向基本情况靠近)

c) 想着递归结果迟早变成一个数值。

一个简单的递归：

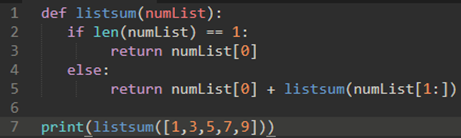
a) 当前列表长度为1的时候结束递归

b) numlist[1:]每次都减少了一个元素

c) numlist[1:]迟早会变成24(3+5+7+9)，然后加上numlist[0]，最后return出来。

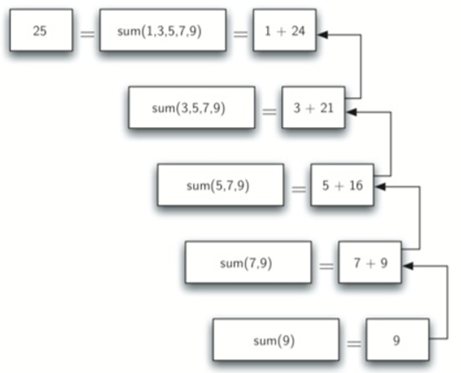
\54. 递归的三定律：

a) 递归算法必须具有基本情况。

b) 递归算法必须改变其状态并向基本情况靠近。

c) 递归算法必须以递归方式调用自身。

其中重点和难点是第二点：
为了遵守第二定律，我们必须将算法向基本情况的状态改变。
状态的改变意味着该算法正在使用的一些数据被修改。通常，表示问题的数据在某种程度上变小。在listsum算法中，我们的主要数据结构是一个列表，因此我们必须将我们的状态转换工作集中在列表上。因为基本情况是长度1的列表，所以朝向基本情况的自然进展是缩短列表。

\55. 示例二：使用递归将数字转为str:

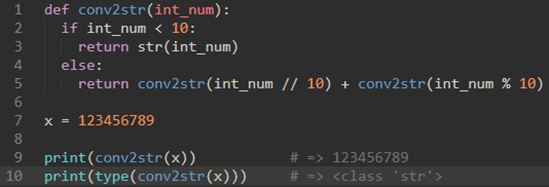
a) 什么时候结束递归:
当int_num小于10的时候

b) 递归算法必须改变其状态并向基本情况靠近：
使用mod不断弹出个位，这样int_num每次就会减少一位数。

c) 想着递归结果迟早变成一个数值：
迟早会变成一个字符，使用加号将其加起来。

上面代码稍微修改一下就可以变成进制转换函数

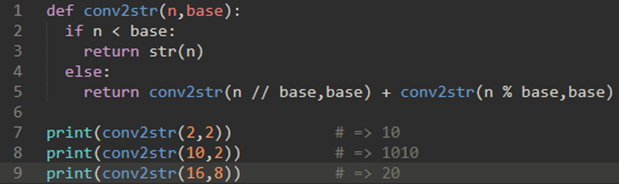
再修改一下，让该函数支持16进制：

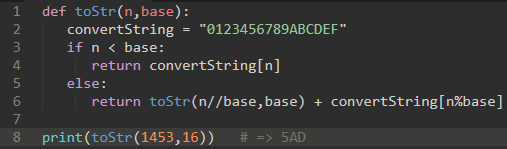
\56. 栈帧：实现递归
上面的代码如果使用栈的话：

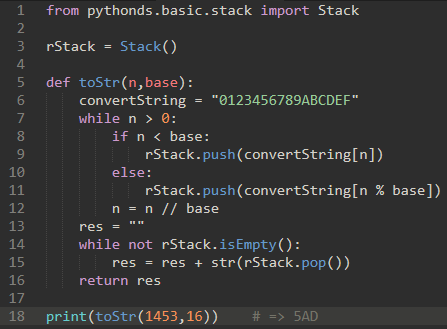
当在Python中调用函数时，会分配一个栈来处理函数的局部变量。
当函数返回时，返回值留在栈的顶部，以供调用函数访问。
下图说明了第4行返回语句后的调用栈。

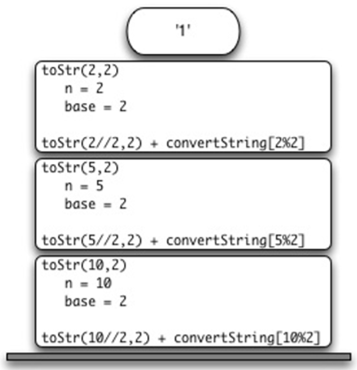
对toStr(2//2,2)的调用在栈上返回值为“1”。然后，在表达式“1”+convertString[2％2]中使用此返回值替换函数调用(toStr(1,2))，这将在栈顶部留下字符串“10”。这样，Python调用栈就代替了使用的栈。

栈帧还为函数使用的变量提供了一个作用域。
即使我们重复地调用相同的函数，每次调用都会为函数本地的变量创建一个新的作用域。

\57. 可视化递归:
python内置了一个插图工具：turtle(乌龟)模块

示例：使用递归绘制螺旋：

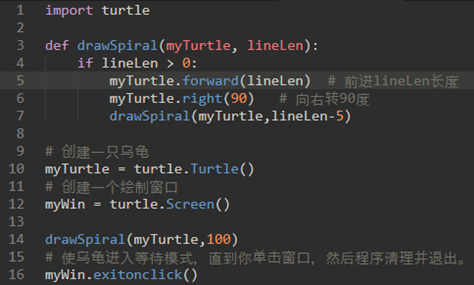
效果：

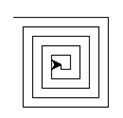
\58. 使用递归绘制分形树：
分形：当你看着它时，无论你放大多少，分形有相同的基本形状。（即使一个小树枝也有一个整体树的相同的形状和特征）

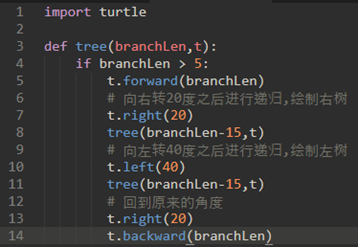
因为分形树就是相似的形状，所以使用递归，每次都减少绘制的长度。
调用：

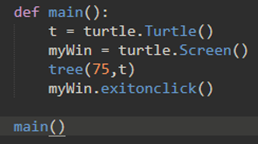
效果如下：

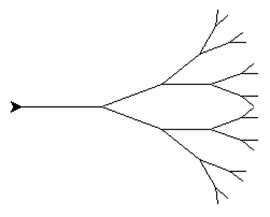
注意绘制步骤：先绘制完下面的子树，再去绘制上面的子树。

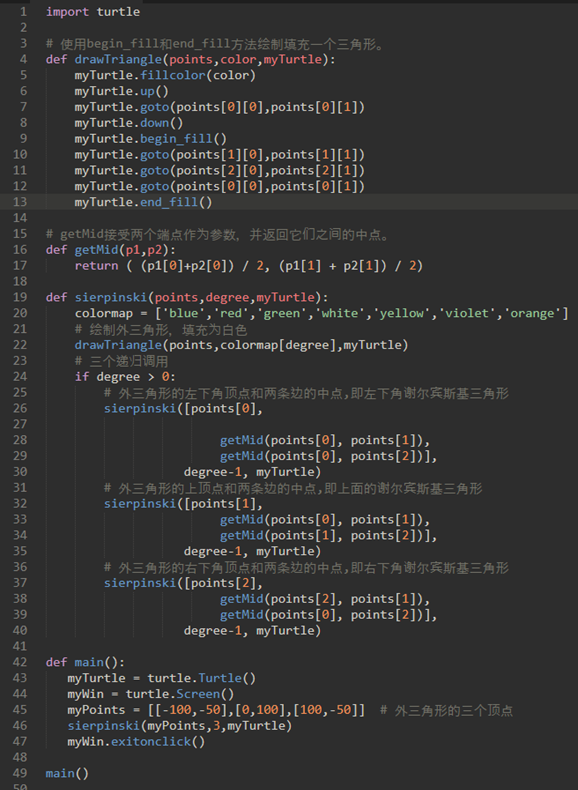
\59. 谢尔宾斯基三角形：
运用三路递归算法：从一个大三角形开始。通过连接每一边的中点，将这个大三角形分成四个新的三角形。忽略刚刚创建的中间三角形，对三个小三角形中的每一个应用相同的过程。

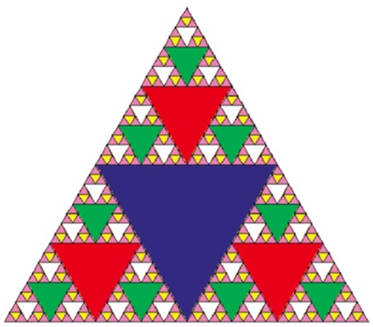
基本情况被任意设置为我们想要将三角形划分成块的次数。把这个数字称为分形的“度”。
每次我们进行递归调用时，我们从度中减去1，直到0。当我们达到0度时，我们停止递归。

谢尔宾斯基分为左下，上，右下三种，我们的目标：
递归完左下角最小的三角形，再递归上面的三角形，最后才是右下的三角形。

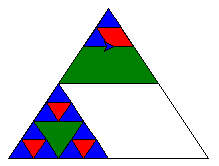
代码如下：

\60. 汉诺塔游戏：
思路：从下到上考虑这个问题。
五个盘子的塔。如果已经知道如何将四个盘子移动到杆二上，那么你可以轻松地将最底部的盘子移动到杆三，然后再将四个盘子从杆二移动到杆三。
但是如果你不知道如何移动四个盘子怎么办？假设你知道如何移动三个盘子到杆三;那么很容易将第四个盘子移动到杆二，并将它们从杆三移动到它们的顶部。
但是如果你不知道如何移动三个盘子呢？如何将两个盘子移动到杆二，然后将第三个盘子移动到杆三，然后移动两个盘子到它的顶部？
但是如果你还不知道该怎么办呢？最简单的汉诺塔是一个盘子的塔。在这种情况下，我们只需要将一个盘子移动到其最终目的地。一个盘子的塔将是我们的基本情况。

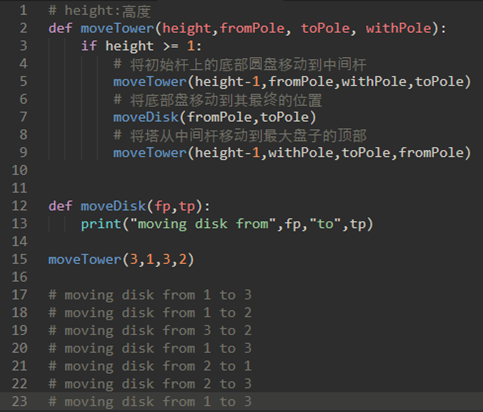
\61. 使用中间杆将塔从起始杆移动到目标杆的步骤

a) 使用目标杆将height-1的塔移动到中间杆。

b) 将剩余的盘子移动到目标杆。

c) 使用起始杆将height-1的塔从中间杆移动到目标杆。

代码如下:579分别对应abc

\62. 探索迷宫

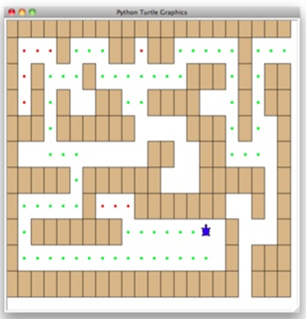
为了使问题容易些，我们假设我们的迷宫被分成“正方形”。
搜索过程如下：

a) 从起始位置，我们将首先尝试向北一格，然后从那里递归地尝试我们的程序。

b) 如果我们通过尝试向北作为第一步没有成功，我们将向南一格，并递归地重复我们的程序。

c) 如果向南也不行，那么我们将尝试向西一格，并递归地重复我们的程序。

d) 如果北，南和西都没有成功，则应用程序从当前位置递归向东。

e) 如果这些方向都没有成功，那么没有办法离开迷宫，我们失败。

\63. 假设我们第一步是向北走。按照我们的程序，我们的下一步也将是向北。
但如果北面被一堵墙阻挡，我们必须看看程序的下一步，并试着向南。不幸的是，向南使我们回到原来的起点。如果我们从那里再次应用递归过程，我们将又回到向北一格，并陷入无限循环。所以，我们必须有一个策略来记住我们去过哪。在这种情况下，我们假设有一袋面包屑可以撒在我们走过的路上。如果我们沿某个方向迈出一步，发现那个位置上已经有面包屑，我们应该立即后退并尝试程序中的下一个方向。

\64. 在这种算法中，有四种基本情况要考虑：

a) 乌龟撞到了墙。由于这一格被墙壁占据，不能进行进一步的探索。

b) 乌龟找到一个已经探索过的格。我们不想继续从这个位置探索，否则会陷入循环。

c) 我们发现了一个外边缘，没有被墙壁占据。换句话说，我们发现了迷宫的一个出口。

d) 我们探索了一格在四个方向上都没有成功

\65. 迷宫没看，跳过了（98-102）

\66.

\67.

\68.

\69. 动态规划：
某国有1,5,10,25元面额的硬币，现在要支付63元，如何使用最少的硬币数量？

使用递归：

a) 基线条件：支付金额等于硬币面值

b) 递归条件：每次都减去某个硬币面值

代码：

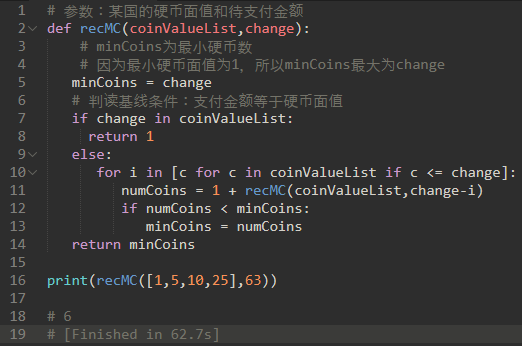
上面的算法是非常低效的。事实上，它需要67,716,925个递归调用来找到最佳方案。

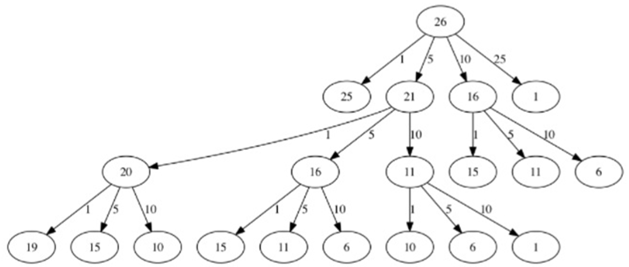
图中的每个节点对应于对recMC的调用。节点上的标签表示硬币数量的变化量。箭头上的标签表示我们刚刚使用的硬币。
通过跟随图表，我们可以看到硬币的组合。主要的问题是我们重复做了太多的计算。例如，该图表示该算法重复计算了至少三次支付15美分。这些计算找到15美分的最佳硬币数量的步骤本身需要52个函数调用。显然，我们浪费了大量的时间和精力重新计算旧的结果。

\70. 减少我们工作量的关键是记住一些过去的结果。一个简单的解决方案是将最小数量的硬币的结果存储在表中。然后在计算新的最小值之前，我们首先检查表，看看结果是否已知。如果表中已有结果，我们使用表中的值。

eg:6元的最小支付硬币数为2（5元+1元）

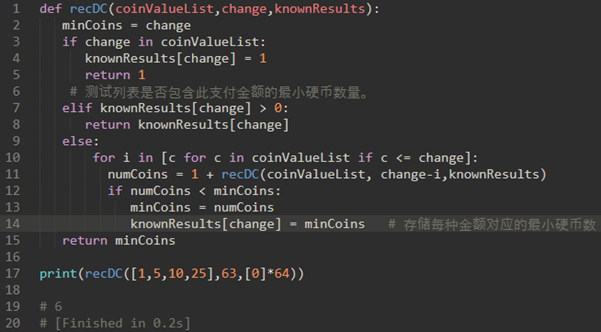
上面代码，我们通过使用称为记忆化的技术来提高我们的程序的性能，或者更常见的叫做缓存。

\71. 现在我们将使用动态规划的方法来处理问题：

硬币面额是1,5,10,25，要支付11元的思路：

a) 一个一分钱硬币加上11-1=10分（1）的最小硬币数，即1+1=2

b) 一个五分钱硬币加上11-5=6分（2）的最小硬币数，即1+2=3

c) 一个十分钱硬币加上11-10=1分（1）最小硬币数，即1+1=2

简单来说，就是使用之前在《算法图解》上说的，看11元可以由什么组成：1元+10元，2元+9元，3元+8元…

需要注意的是，2元+9元表示的是：支付2元的最小硬币数+支付9元的最小硬币数。

\72. 用一个动态规划算法来解决我们的找零问题：

\73.

\74. 又tm的看不懂，跳过吧105-107

\75.

\76.

\77.

\78.

\79.

\80.

\81.

\82. 完全看不懂的页数：

a) （55到59页）

b) （98-102）

c) （105-107）