第五章:排序和搜索
- 顺序查找

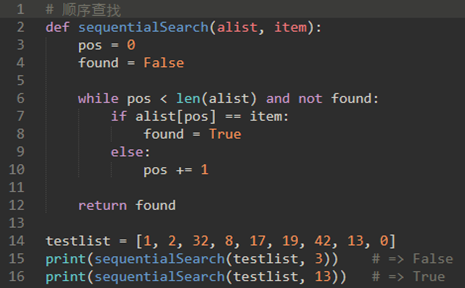
\2. 顺序查找分析:
平均来说,我们会在列表的一半找到该项;也就是说,我们将比较n/2项。因此顺序查找的复杂度是O(n)。

\3. 对于有序列表来说,“查找不存在某个元素”的操作比较有优势: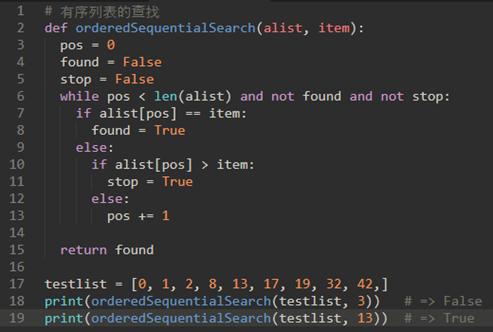

\4. 二分查找:
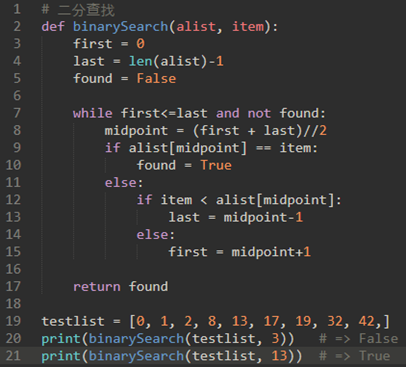
二分算法是分而治之策略的一个很好的例子。
分和治意味着我们将问题分成更小的部分,以某种方式解决更小的部分,然后重新组合整个问题以获得结果。
当我们执行列表的二分查找时,我们首先检查中间项。如果我们正在搜索的项小于中间项,我们可以简单地对原始列表的左半部分执行二分查找。同样,如果项大,我们可以执行右半部分的二分查找。无论哪种方式,都是递归调用二分查找函数。
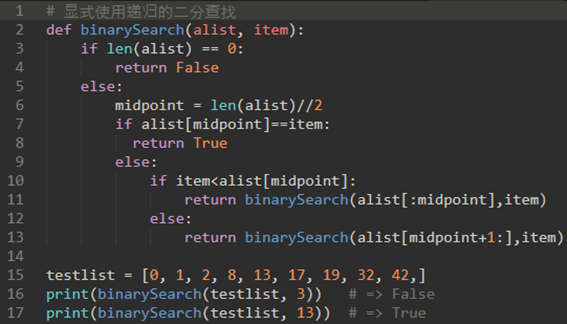
\5. 二分查找分析:二分查找是O(logN)。
但是,观察下面的return,这里使用了切片

我们知道Python中的slice运算符是O(k)。
这意味着使用slice的二分查找将不会在严格的对数时间执行。
一般情况下,二分查找的用处比较有限,因为排序的成本比较高,对于大列表来说更是如此,从一开始就执行顺序查找可能是最好的选择。
\6. Hash查找:
哈希表的每个位置,通常称为一个槽,可以容纳一个项,并且由从0开始的整数值命名。
例如,我们有一个名为0的槽,名为1的槽,名为2的槽,以上。
最初,哈希表不包含项,因此每个槽都为空。

项和该项在散列表中所属的槽之间的映射被称为hash函数。
hash函数将接收集合中的任何项,并在槽名范围内(0和m-1之间)返回一个整数。
\7. 现在我们使用名为“求余法”的哈希函数:
将一个项除以表大小,返回剩余部分作为其散列值
这里表的大小为11,所以(h(item)=item%11)

eg:54的哈希值为54%11,为10
26的哈希值为26%11,为4
一旦计算了哈希值,我们可以将每个项插入到指定位置的哈希表中:

负载因子:通常表示为λ=项数/表大小,在这个例子中,λ=6/11。
根据散列函数,两个或更多项将需要在同一槽中。(如44和77)这种现象被称为“冲突”。
\8. 这就能解释为什么散列表的复杂度为O(1):
当我们要搜索一个项时,我们只需使用哈希函数来计算项的槽名称,然后检查哈希表以查看它是否存在。
给定项的集合,将每个项映射到唯一槽的散列函数被称为完美散列函数。
\9. 我们的目标是创建一个散列函数,最大限度地减少冲突数,易于计算,并均匀分布在哈希表中的项。有很多常用的方法来扩展简单余数法。我们将在这里介绍其中几个。
分组求和法将项划分为相等大小的块(最后一块可能不是相等大小)。然后将这些块加在一起以求出散列值。
例如,如果我们的项是电话号码436-555-4601,我们将取出数字,并将它们分成2位数(43,65,55,46,01)。43+65+55+46+01,我们得到210。我们假设哈希表有11个槽,那么我们需要除以11。在这种情况下,210%11为1,因此电话号码436-555-4601散列到槽1。一些分组求和法会在求和之前每隔一个反转。对于上述示例,我们得到43+56+55+64+01=219,其给出219%11=10。
平方取中法。我们首先对该项平方,然后提取一部分数字结果。
例如,如果项是44,我们将首先计算44^2=1936。通过提取中间两个数字93,我们得到5(93%11)。
我们还可以为基于字符的项(如字符串)创建哈希函数。词cat可以被认为是ascii值的序列。

然后,获取这三个ascii值,将它们相加,并使用余数方法获取散列值。
代码如下:
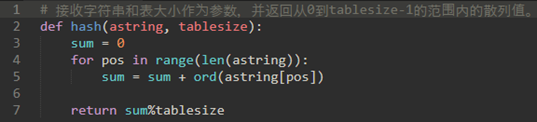
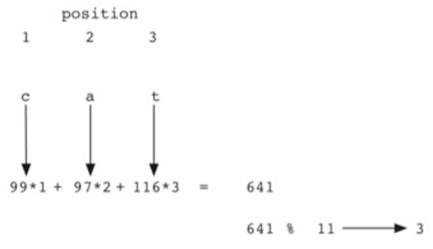
如果还需要改进的话,我们可以使用字符的位置作为权重。,
如:第一位权重为1,二位权重为2,三位权重为3
\10. 当两个项散列到同一个槽时,我们必须有一个系统的方法将第二个项放在散列表中。这个过程称为冲突解决。
解决冲突的一种方法是查找散列表,尝试查找到另一个空槽以保存导致冲突的项。一个简单的方法是从原始哈希值位置开始,然后以顺序方式移动槽,直到遇到第一个空槽。
注意,我们可能需要回到第一个槽(循环)以查找整个散列表。这种冲突解决过程被称为开放寻址,因为它试图在散列表中找到下一个空槽或地址。通过系统地一次访问每个槽,我们执行称为线性探测的开放寻址技术。
eg:原先的散列表如下:

现在插入44,55,20:

当我们尝试将44放入槽0时,发生冲突。在线性探测下,我们逐个顺序观察,直到找到位置。在这种情况下,我们找到槽1。
再次,55应该在槽0中,但是必须放置在槽2中,因为它是下一个开放位置。
值20散列到槽9。由于槽9已满,我们进行线性探测。我们访问槽10,0,1和2,最后在位置3找到一个空槽。
\11. 一旦我们使用开放寻址和线性探测建立了哈希表,我们就必须使用相同的方法来搜索项。
假设想查找项93。计算哈希值,得到5。查看槽5得到93,返回True。
假设想查找项20,哈希值为9,而槽9当前项为31。我们不能简单地返回False,因为我们知道可能存在冲突。我们现在被迫做一个顺序搜索,从位置10开始寻找,直到我们找到项20或找到一个空槽。
\12. 线性探测缺点是聚集的趋势:项在表中聚集。
这意味着如果在相同的散列值处发生很多冲突,则将通过线性探测来填充多个周边槽。这将影响正在插入的其他项,正如我们尝试添加上面的项20时看到的。必须跳过一组值为0的值,最终找到开放位置。
处理聚集的一种方式是扩展线性探测技术:
线性探测的开放寻址是遇到冲突的时候顺移一个槽。而扩展线性探测是顺移N个槽:
eg:使用加3探头:即发生冲突的时候跳三个槽,直到找到空槽。
原散列表:

现在插入44,55,20:

对比发现,这将比较好的解决项在表中聚集现象
\13. 在冲突后寻找另一个槽的过程叫重新散列。
使用简单的线性探测,rehash函数是 
所以线性探测的开放寻址的rehash函数为: 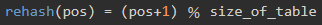
加3探头的扩展线性探测的rehash函数为: 
重要的是要注意,“跳过”的大小(探头大小)必须使得表中的所有槽最终都被访问。否则,表的一部分将不被使用。为了确保这一点,通常建议表大小是素数。
\14. 线性探测思想的一个变种称为二次探测。
就是不再跳过固定的值,而是跳过变化的值。我们使用rehash函数,将散列值递增1,3,5,7,9,依此类推。这意味着如果第一哈希值是h,则连续值是h+1,h+4,h+9,h+16,等等。
\15. 用于处理冲突问题的替代方法是允许每个槽保持对项的集合(或链)的引用。
链接允许许多项存在于哈希表中的相同位置。当发生冲突时,项仍然放在散列表的正确槽中。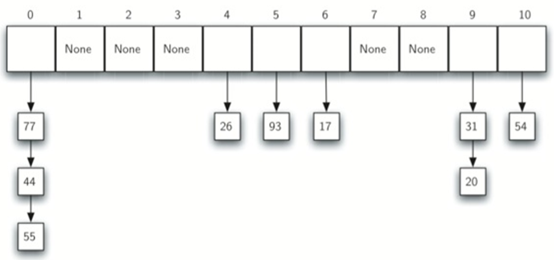
\16. 实现map抽象数据类型(映射对象):
map抽象数据类型结构是键与值之间的关联的无序集合。map中的键都是唯一的,因此键和值之间存在一对一的关系。操作如下:
a) Map()创建一个新的map。它返回一个空的map集合。
b) put(key,val)向map中添加一个新的键值对。如果键已经在map中,那么用新值替换旧值。
c) get(key)给定一个键,获取存储在map中的值或None。
d) del使用del map[key]形式的语句从map中删除键值对。
e) len()返回存储在map中的键值对的数量。
f) in对于key in ma语句,如果给定的键在map中返回True,否则为False。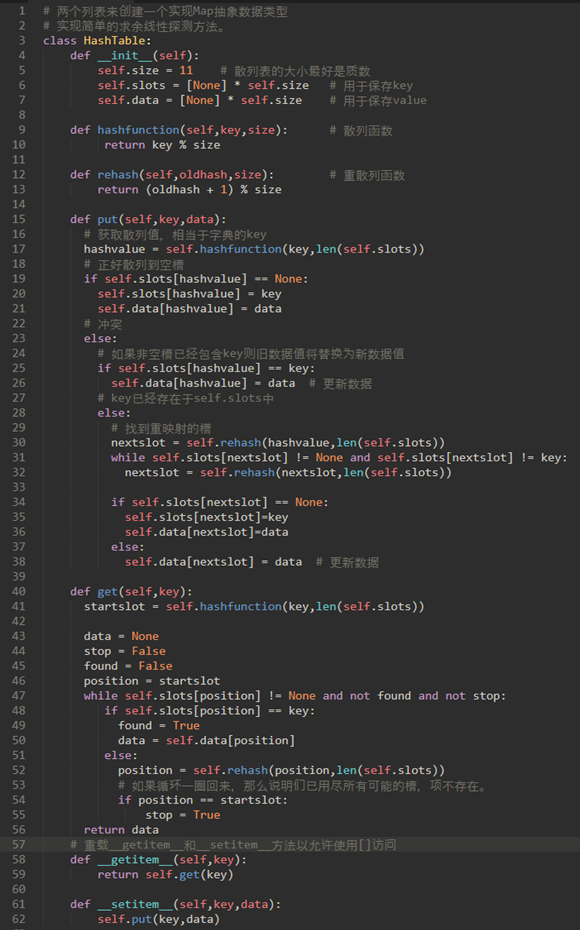
上面代码,需要注意26行和38行,如果非空槽已经包含key,则旧数据值将替换为新数据值。
使用:
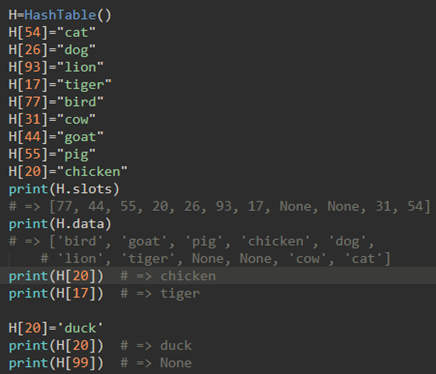
\17. hash法分析:
因为冲突,hash表的复杂度不是真正的O(1)。
分析散列表最重要的信息是负载因子λ。
对于使用具有线性探测的开放寻址的成功搜索,平均比较数大约为1/2(1+1/(1-λ)),不成功的搜索为1/2(1+(1/1-λ)^2)如果我们使用链接,则对于成功的情况,平均比较数目是1+λ/2,如果搜索不成功,则简单地是λ比较次数。
第六章:排序
\18. 冒泡排序:
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序

从上面示意图可知,冒泡排序需要多次遍历。
如果在列表中有n个项目,则第一遍有n-1个项需要比较。所需的遍历的总数将是 n-1。
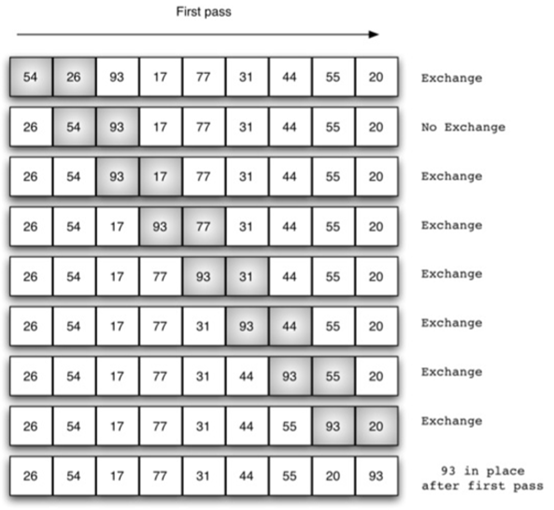
所以,冒泡排序每一次遍历都会将最大/最小的排在正确的位置。
\19. 代码实现:
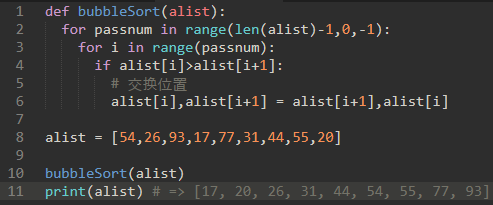
要注意,passnum是倒序,这样才能让alist[i+1]不会indexError

\20. 分析排序的重要标准:
a) 比较次数。
b) 交换次数。
冒泡排序的复杂度分析:
不管项如何在初始列表中排列,将进行n-1次遍历以排序大小为n的列表。所以比较次数不变。
最好的情况下,如果列表已经排序,则不会进行交换。但是在最坏的情况下,每次比较都会导致交换元素。平均来说,我们交换了一半时间。
所以复杂度为O(n^2)。
冒泡排序通常被认为是最低效的排序方法,
因为它必须在最终位置被知道之前交换项。这些“浪费”的交换操作是非常昂贵的。
然而,因为冒泡排序遍历列表的整个未排序部分,它有能力做大多数排序算法不能做的事情:
如果在遍历期间没有交换,则我们知道该列表已排序。如果发现列表已排序,可以修改冒泡排序提前停止。这意味着对于只需要遍历几次列表,冒泡排序具有识别排序列表和停止的优点。
\21. 所以说,冒泡排序是可修改的,被称为“短冒泡排序”:
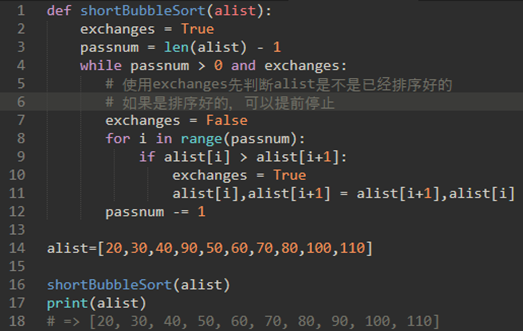
所以,如果alist是已经排序完成的话,就不会进行下一次遍历,可以直接退出了。
\22. 选择排序:遍历,每次取最高项。
选择排序改进了冒泡排序,每次遍历列表只做一次交换。一个选择排序在他遍历时寻找最大的值,并在完成遍历后,将其放置在正确的位置。
与冒泡排序一样,在第一次遍历后,最大的项在正确的地方。第二遍后,下一个最大的就位。
遍历n-1次排序n个项,因为最终项必须在第(n-1)次遍历之后。

代码实现:
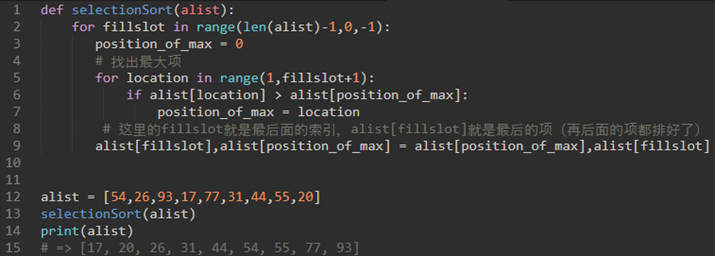
或者:
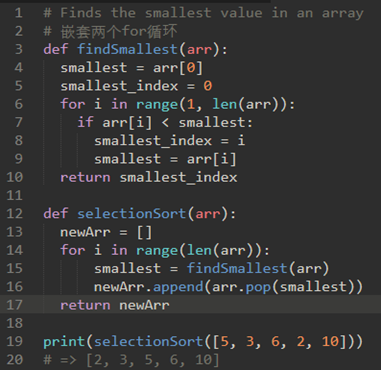
\23. 嵌套两次循环,所以选择排序也是O(n^2)。然而,由于交换数量的减少,选择排序通常在执行得更快。
\24. 插入排序:
a) 从第一个元素开始,该元素可以认为已经被排序。
b) 取出下一个元素,在已经排序的元素序列中从后向前扫描。
c) 如果该元素(已排序)大于新元素,将该元素移到下一位置。
d) 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置。
e) 将新元素插入到该位置中。
f) 重复步骤2。
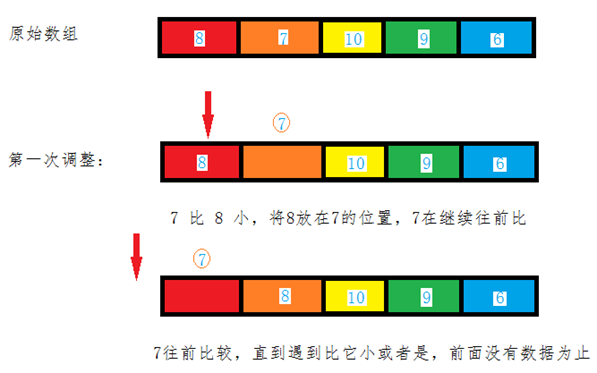
从上面步骤我们得知,插入排序始终在列表的较低位置维护一个排序的子列表。然后将每个新项“插入”回先前的子列表。
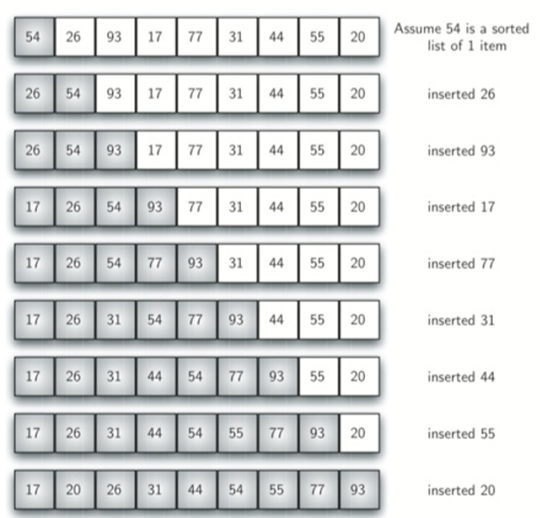
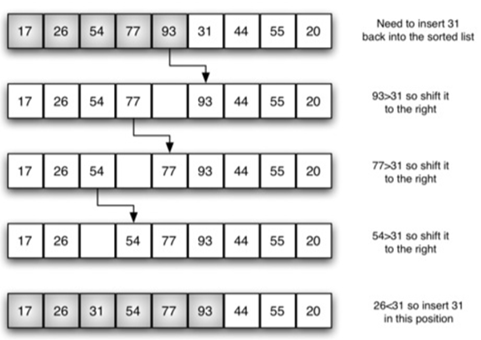
具体的移动步骤如下:
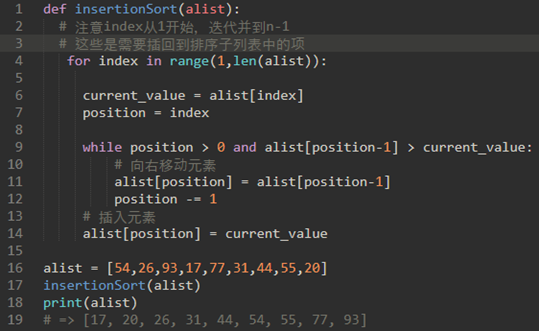
\25. 代码实现:
\26. 插入排序嵌套两次循环,复杂度是O(n^2)。
然而,排序的列表的情况下,每次通过只需要进行一次比较。
关于移位和交换:移位操作只需要交换大约三分之一的处理工作,因为仅执行一次分配。
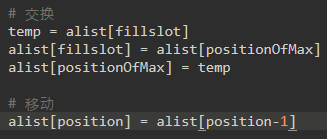
在基准研究中,插入排序有非常好的性能。
\27. 希尔排序(递减递增排序):
实质就是分组插入排序
基本思想:
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时 间效率上比前两种方法有较大提高。
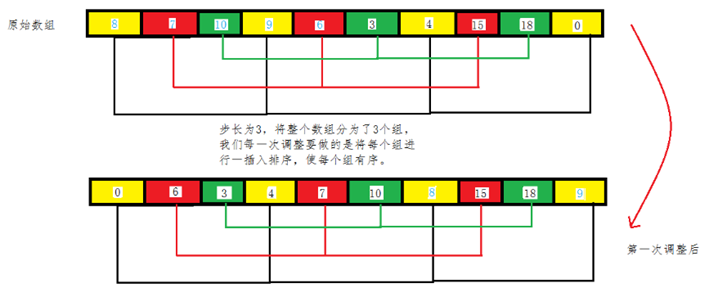
简单来说,希尔排序使用增量i(称为gap),通过选择i个项的所有项来创建子列表,每个子列表使用插入排序进行排序。
如下为9项大小的表使用三的增量,分为三个子序列:

每个子列表使用插入排序进行排序。
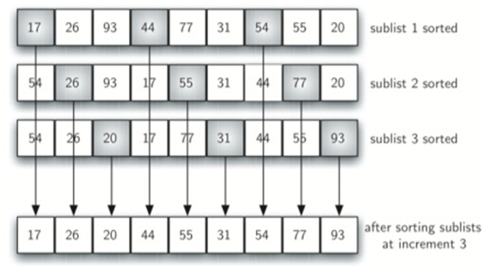
然后使用标准插入排序。
注意,通过执行之前的子列表排序,我们减少了 将列表置于其最终顺序所需的移位操作的总数。
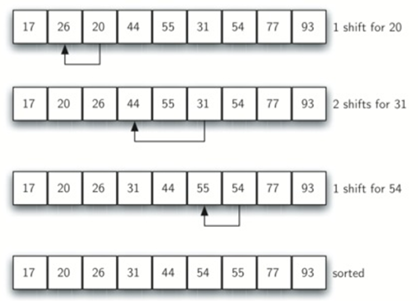
所以说,增量的选择方式是希尔排序的独特特征。
\28. 希尔排序的代码实现:
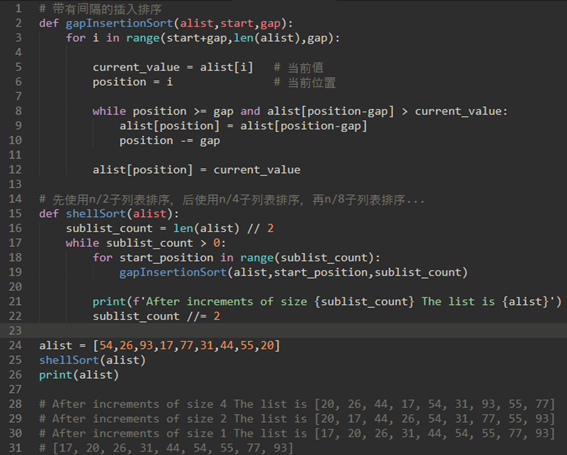
希尔排序的在复杂度O(n^3/2)
\29. 归并排序:
归并排序是一种递归算法,不断将列表拆分为一半。如果列表为空或有一个项,则按定义(基本情况)进行排序。如果列表有多个项,我们分割列表,并递归调用两个半部分的合并排序。
说人话:将数据进行两两分组,每组之间进行排序,每小组排序完成后,再见这些有序的小组之间进行合并排序,知道最后合并完成。

每两个分组,然后每组各自排序:

每四个分组,然后每组各自排序:

第三趟分组,然后排序:

示意图:先分组:
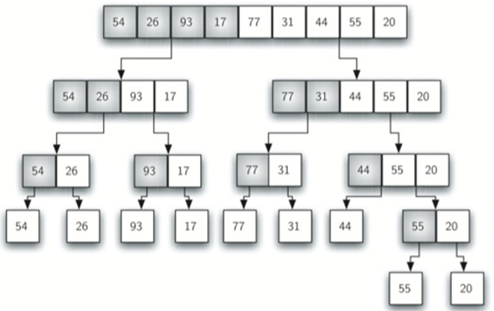
后归并:
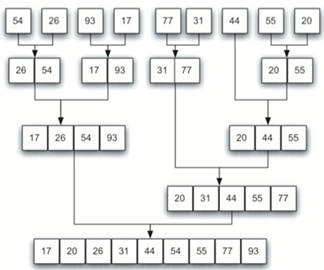
\30. 代码实现:
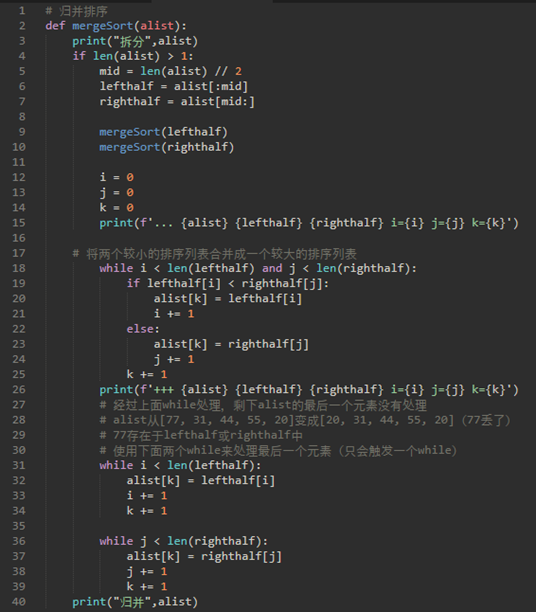
这里代码很不好理解,配合执行结果观察:

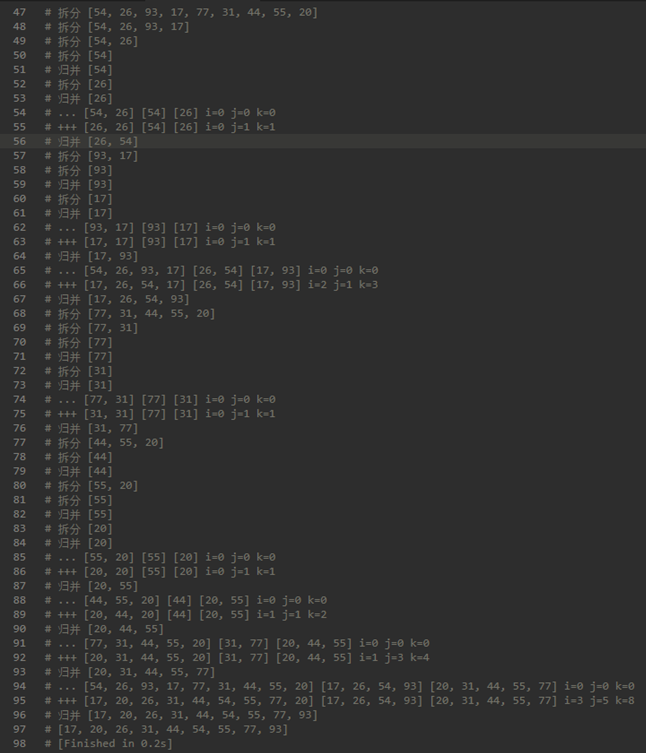
总结:
归并排序逻辑上就是:先拆分,后归并。
这里的拆分就可以使用递归。
上面代码有三个while,第一个while处理了90%的工作,但是把alist的最后一个元素弄丢了。所以需要后面两个while来处理。(两个while只会触发一个)
\31. 归并排序的性能:
归并排序分为两步:拆分和归并。
拆分:将列表划分为一半需要log^n次
归并:大小为n的列表的合并操作需要n个操作
所以复杂度为nlog^n
注意,mergeSort函数需要额外的空间来保存两个半部分,因为它们是使用切片操作提取的。
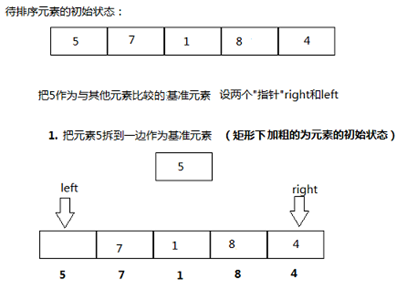
\32. 快速排序:
快速排序使用分而治之来获得与归并排序相同的优点,而不使用额外的存储。
快速排序选择一个值来拆分列表,该值称为。注意:枢轴值属于最终排序列表(通常称为拆分点)的实际位置。
回顾之前的算法:
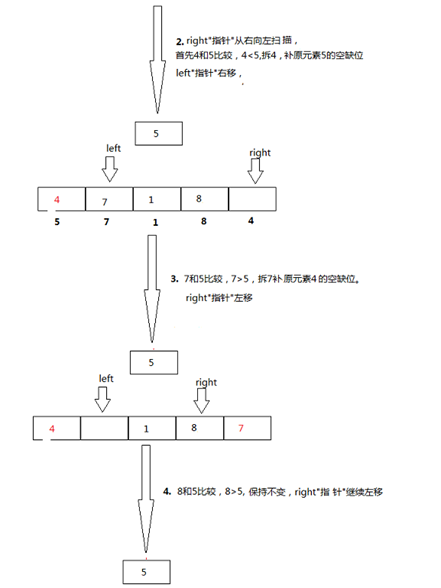
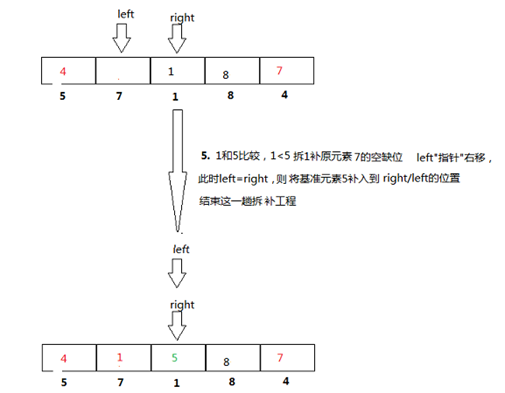
代码:
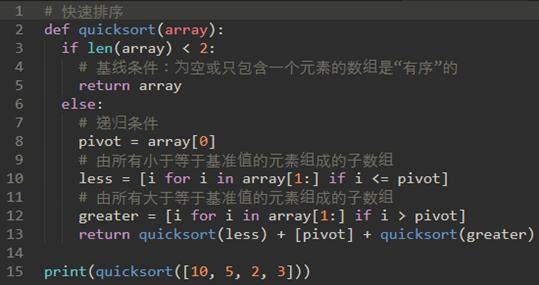
上面代码实际可行,但是效率较低,改用下面的快速排序(原理一样,但是步骤不一样):
我们首先增加左标记,直到找到一个大于枢轴值的值。然后递减右标,直到找到小于枢轴值的值。两个标记停在93和20。交换这两个项目,然后重复该过程。
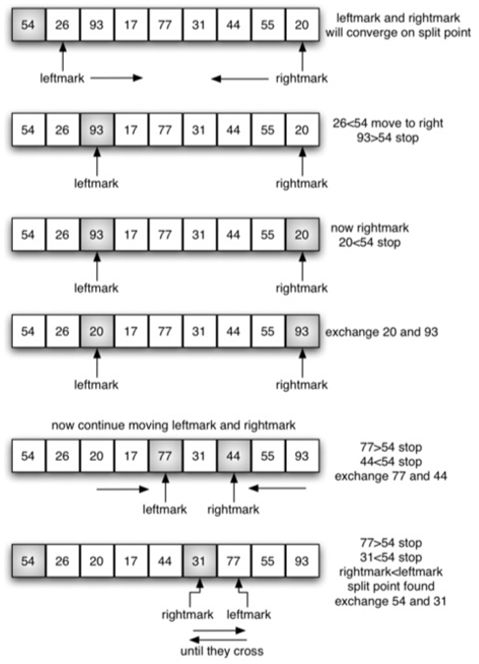
代码如下:
注意:当循环结束时,左右标记交错而过,此时的右标记就是列表的分割点。
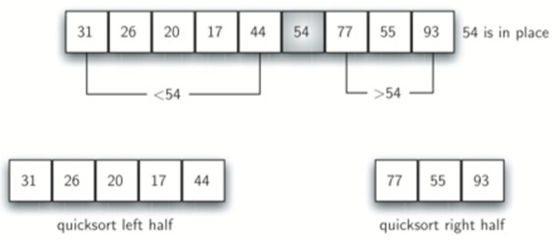
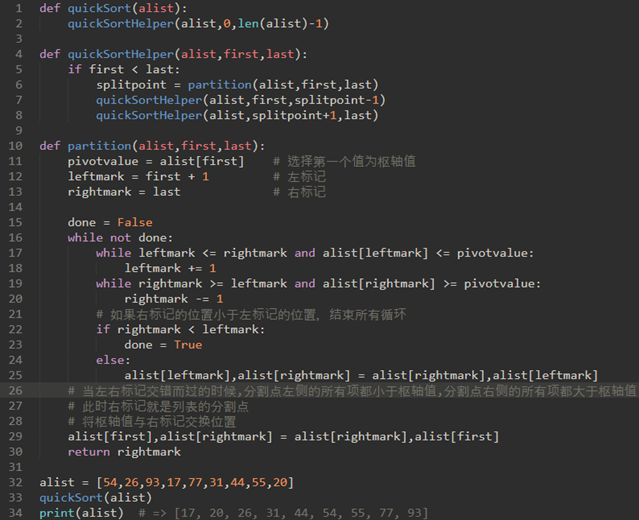
quickSortHelper的基线条件是first=last,也就是说左标记和右标记重合,也就是alist长度为1。
\33. 快速排序的性能分析:
和之前说的一样,介于O(nlogN)与O(n^2)之间
中值三技术可以减轻不均匀分割的可能性:
选择枢轴值时,考虑列表中的第一个,中间和最后一个元素。
在示例中,这些是54,77和20.现在选择中值54作为枢轴值。
简单来讲,就是:
枢轴值 = middle(第一个元素,中间元素,最后一个元素)
第六章:树
\34. 树的属性:
a) 树是分层的
b) 一个节点的所有子节点独立于另一个节点的子节点。
c) 每个叶节点是唯一的。
\35. 其实html代码就是树:
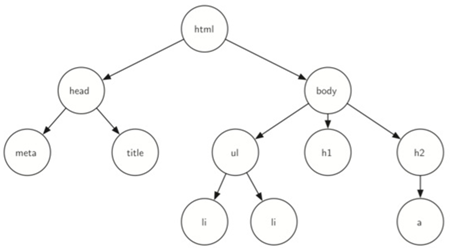
\36. 正式定义树及其组件:
a) 节点:是树的基本部分。有另一个名称:“键”。节点也可以有附加信息。我们将这个附加信息称为“有效载荷”。虽然有效载荷信息不是许多树算法的核心,但在利用树的应用中通常是关键的。
b) 边:是树的另一个基本部分。边连接两个节点以显示它们之间存在关系。每个节点(除根之外)都恰好从另一个节点的传入连接。每个节点可以具有多个输出边。
c) 根:是树中唯一没有传入边的节点。
d) 路径:是由边连接节点的有序列表。例如,Mammal→→Carnivora→→Felidae→→Felis→→Domestica是一条路径。
e) 子节点:具有来自相同传入边的节点c的集合称为该节点的子节点。
f) 父节点:具有和它相同传入边的所连接的节点称为父节点。
g) 兄弟:树中作为同一父节点的子节点的节点被称为兄弟节点。
h) 子树:是由父节点和该父节点的所有后代组成的一组节点和边。
i) 叶节点:是没有子节点的节点。(就是树的最后一层节点)
j) 层数:节点n的层数为从根结点到该结点所经过的分支数目。(根节点的层数为零)
k) 高度:等于树中任何节点的最大层数
\37. 使用列表实现树:
将根节点的值存储为列表的第一个元素。列表的第二个元素本身将是一个表示左子树的列表。列表的第三个元素将是表示右子树的另一个列表。
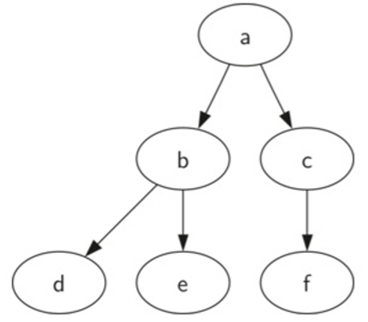
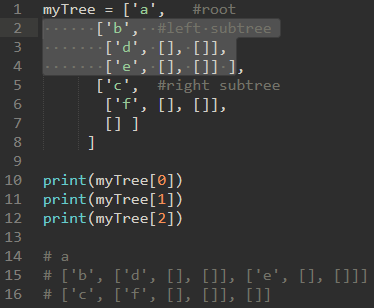
树的根是myTree[0],
根的左子树是myTree[1],
右子树是myTree[2]
该列表方法的一个非常好的属性是表示子树的列表的结构遵守树定义的结构:结构本身是递归的!具有根值和两个空列表的子树是叶节点。列表方法的另一个很好的特性是它可以推广到一个有许多子树的树。在树超过二叉树的情况下,另一个子树只是另一个列表。
\38. 使用列表模拟树,代码如下:
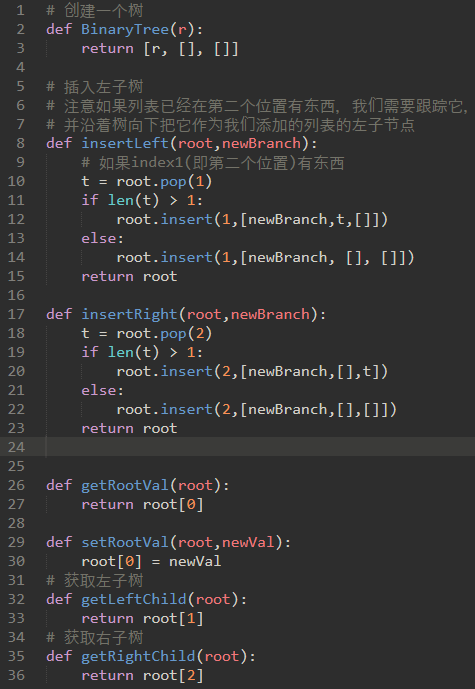
\39. 节点表示:
第二种表示树的方法使用节点和引用。
在这种情况下,我们将定义一个具有根值属性的类,以及左和右子树。
\40. 代码实现:
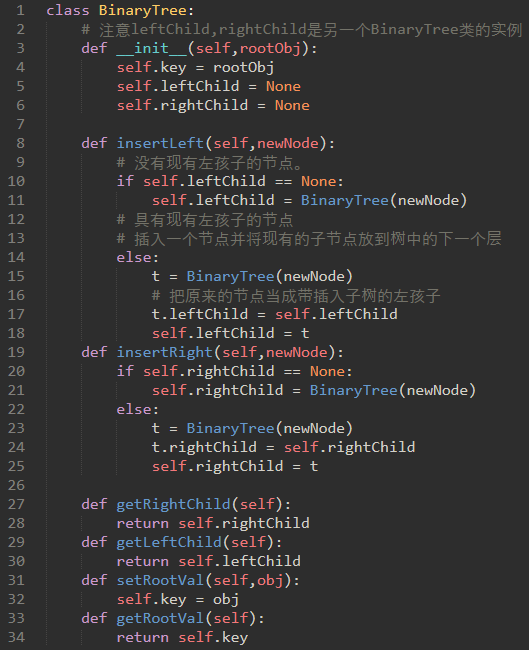
运用: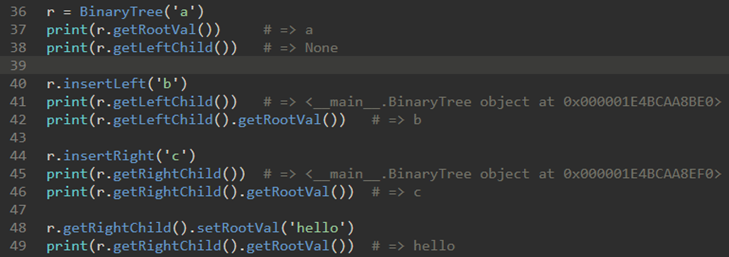
\41. 分析树:
((7+3)*(5-2))使用树来表示:
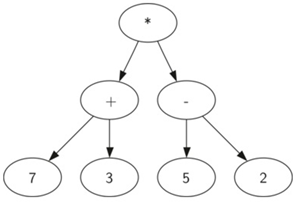
树的层次结构帮助我们了解表达式的求值顺序:
在我们计算顶层乘法之前,我们必须计算子树中的加法和减法。
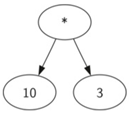
学习目标:
a) 如何从完全括号的数学表达式构建分析树。
b) 如何评估存储在分析树中的表达式。
c) 如何从分析树中恢复原始数学表达式
\42. 思路:
将表达式字符串拆分成符号列表,有四种不同的符号要考虑:
左括号,右括号,运算符和操作数。
每当我们读一个左括号,我们开始一个新的表达式,因此我们应该创建一个新的树来对应于该表达式。相反,每当我们读一个右括号,我们就完成了一个表达式。我们还知道操作数将是叶节点和它们的操作符的子节点。
最后,每个操作符都将有一个左和右孩子。
总结得出:
a) 如果当前符号是’(‘,添加一个新节点作为当前节点的左子节点,并下降到左子节点。
b) 如果当前符号在列表[‘+’,’-‘,’/‘,’*’]中,将当前节点的根值设置为由当前符号表示的运算符。添加一个新节点作为当前节点的右子节点,并下降到右子节点。
c) 如果当前符号是数字,将当前节点的根值设置为该数字并返回到父节点。
d) 如果当前令牌是’)’,转到当前节点的父节点。
\43. 步骤:以(3+(45))为例。
将其拆分为:
[‘(‘,’3’,’+’,’(‘,’4’,’‘,’5’,’)’,’)’]
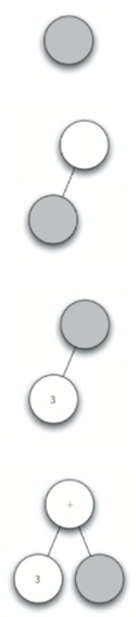 →
→  →
→ 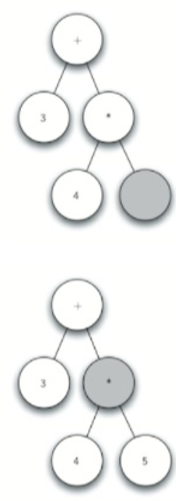
a) 创建一个空树。
b) 读取(作为第一个标记。按规则1,创建一个新节点作为根的左子节点。使当前节点到这个新子节点。
c) 读取3作为下一个符号。按照规则3,将当前节点的根值设置为3,使当前节点返回到父节点。
d) 读取+作为下一个符号。根据规则2,将当前节点的根值设置为+,并添加一个新节点作为右子节点。新的右子节点成为当前节点。
e) 读取(作为下一个符号,按规则1,创建一个新节点作为当前节点的左子节点,新的左子节点成为当前节点。
f) 读取4作为下一个符号。根据规则3,将当前节点的值设置为4。使当前节点返回到父节点。g.读取作为下一个符号。根据规则2,将当前节点的根值设置为,并创建一个新的右子节点。新的右子节点成为当前节点。
g) 读取5作为下一个符号。根据规则3,将当前节点的根值设置为5。使当前节点返回到父节点。
h) 读取)作为下一个符号。根据规则4,使当前节点返回到父节点。
i) 读取)作为下一个符号。根据规则4,使当前节点返回到父节点+。没有+的父节点,所以我们完成创建。
我们需要跟踪当前节点以及当前节点的父节点。如何跟踪父节点?
当遍历树时,保持跟踪父对象的解决方案是栈。每当我们想下降到当前节点的子节点时,我们首先将当前节点压入到栈。当我们想要返回到当前节点的父节点时,我们将父节点从栈中弹出。
\44. 代码如下:
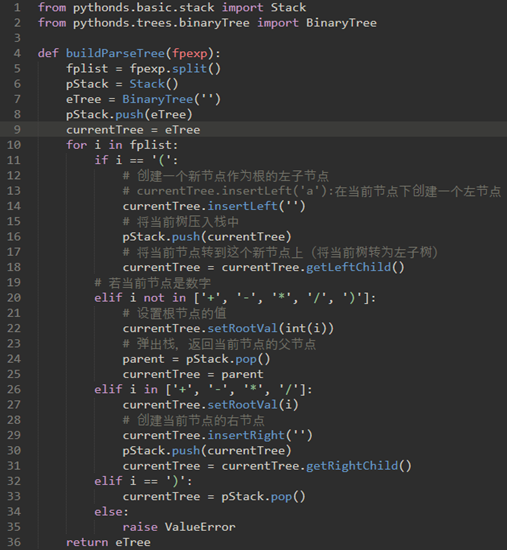
注意:这里的Tree和currentTree其实是树与子树的关系。
这里的树和子树的关系有点像链表的节点和另一个节点的关系。
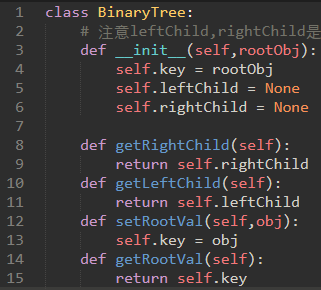
下面第2行,我们使用栈存储的其实是一整个树。第4行,getLeftChild其实就是从一个BinaryTree对象转为另一个BinaryTree对象。
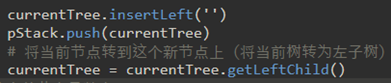
\45. 使用递归来检测树:
a) 对树进行操作的递归算法的基线条件是检查叶节点。在上面的树中,叶节点是操作数。
b) 将函数移向基本情况的递归步骤是在当前节点的左子节点和右子节点上调用evaluate。递归调用有效地使我们沿着树向着叶节点移动。
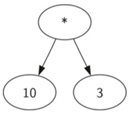
c) 为了将两个递归调用的结果放在一起,我们可以简单地将存储在父节点中的运算符应用于从评估这两个子节点返回的结果。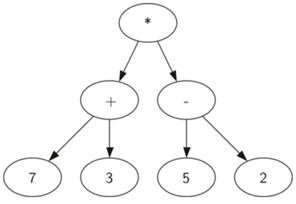 →
→ 
\46. 代码:
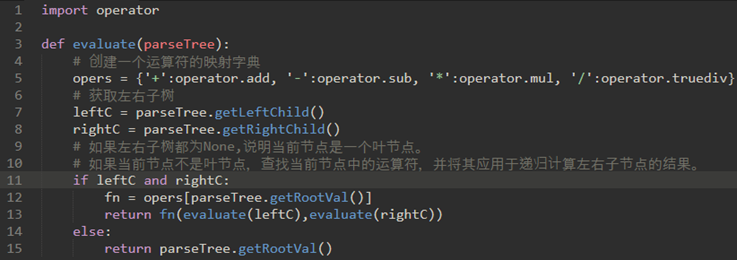
测试:

BinaryTree的左右子树都有定义,保证上面代码的7,8行不会出错:
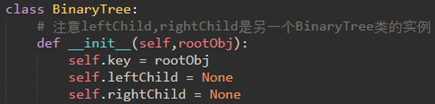
\47. 树的遍历:
有三种常用的模式来访问树中的所有节点:
前序,中序,后序:前中后指的是根节点的访问顺序。(在一开始就访问还是最后访问)
a) 前序:先访问根节点,然后递归地做左侧子树的前序遍历,随后是右侧子树的递归前序遍历
即:根节点-左子树-右子树。
b) 中序:递归地对左子树进行一次遍历,访问根节点,最后递归遍历右子树。
即:左子树-根节点-右子树
c) 后序:递归地对左子树和右子树进行后序遍历,然后访问根节点。
即:左子树-右子树-根节点。
\48. 用树来表示一本书: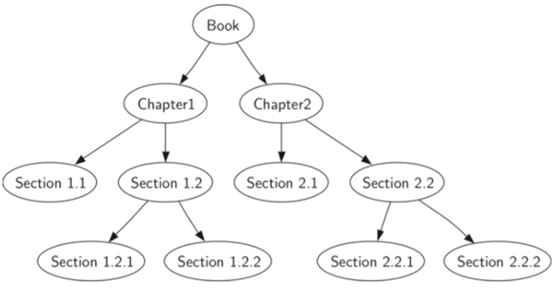
假设你想从前到后读这本书。前序遍历给你正确的顺序:book-chapter1-section1.1-section1.2-section1.2.1-sectioon1.2.2-chapter2-section2.1-section2.2-section2.2.1-section2.2.2
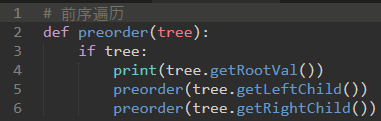
或者:
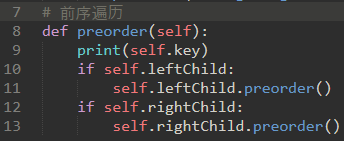
第一段代码很优雅,但是不实用:只能用于遍历树,而第二种可以在遍历的时候添加新的逻辑。
后续遍历:section1.1-section1.2.1-section1.2.2-section1.2-chapter1-section2.1-section2.2.1-section2.2.2-section2.2-chapter2-book
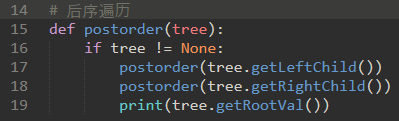
后序遍历的常见用法,计算分析树。
(前面45就是使用后续遍历来计算的:
计算左子树,计算右子树,并通过对操作符的函 数调用在根节点中组合它们。)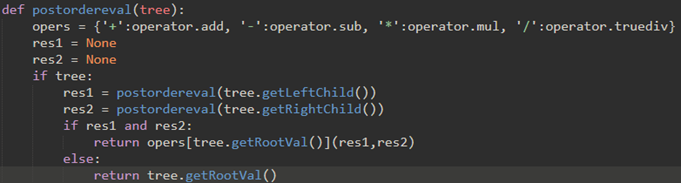
对比上面后续遍历的代码,发现postordereval函数就是将postorder函数的print语句改成其他逻辑而已。
中序遍历:
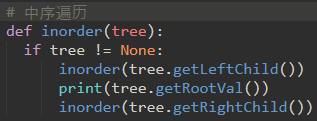
中序遍历:section1.1-chapter1-section1.2.1-section1.2-section1.2.2-book-section2.1-chapter2-section2.2.1-section2.2-section2.2.2
总结:
三种遍历的代码,不同的只有print语句相对于两个递归函数调用位置。
\49. 基于二叉堆的优先队列:
队列的一个重要变种称为优先级队列。
优先级队列的作用就像一个队列,你可以通过从前面删除一个项目来出队。在优先级队列中,队列中的项的逻辑顺序由它们的优先级确定。最高优先级项在队列的前面,最低优先级的项在后面。因此,当你将项排入优先级队列时,新项可能会一直移动到前面。
如果使用列表来实现优先级队列,效果不够理想:插入O(n)并且排序列表是O(nlogn)。
实现优先级队列的经典方法是使用称为二叉堆的数据结构。二叉堆将允许我们在O(logn)中排队和取出队列。
二叉堆有两个常见的变体:
最小堆(其中最小的键总是在前面)。
最大堆(其中最大的键值总是在前面)
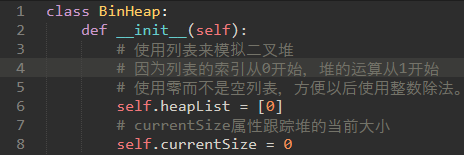
\50. 最小二叉堆实现的基本操作:
a) BinaryHeap()创建一个新的,空的二叉堆。
b) insert(k)向堆添加一个新项。
c) findMin()返回具有最小键值的项,并将项留在堆中。
d) delMin()返回具有最小键值的项,从堆中删除该项。
e) isEmpty()如果堆是空的,返回true,否则返回false。
f) size()返回堆中的项数。
g) buildHeap(list)从键列表构建一个新的堆。
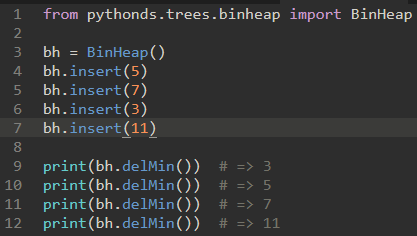
简单来说,最小二叉堆的效果就像一个会自动排序的列表,每次都返回最小值。
\51. 二叉堆实现:
我们利用二叉树的对数性质来表示我们的堆。
为了保证对数性能,我们必须保持树平衡。
通过创建一个完整二叉树来保持树平衡。一个完整的二叉树是一个树,其中每个层都有其所有的节点,除了树的最底层,从左到右填充。
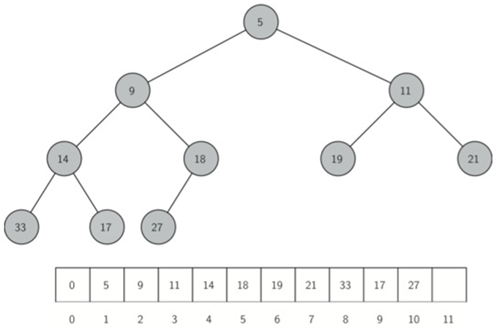
简单来说:
完整二叉树就是除了最后一层,每层都是满的,而且最后一层是从左到右填充的。
\52. 因为完整二叉树的性质,其实我们是可以使用单个列表来表示的(不需要嵌套列表)

父节点的左子节点(在位置p处)是在列表中位置2p中找到的节点。
父节点的右子节点在列表中的位置2p+1。
\53. 堆的排序属性:
在堆中,对于父p的每个节点x,p中的键小于或等于x中的键。
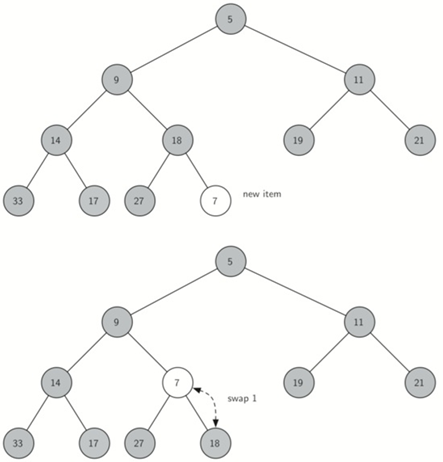
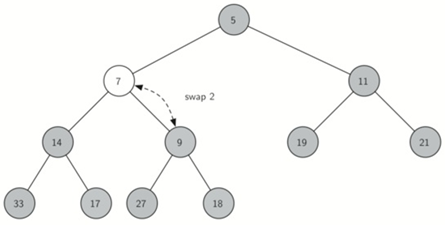
\54. 二叉堆insert需要实现的逻辑:
比较新添加的项与其父项,如果新添加的项小于其父项,则将项与其父项交换。
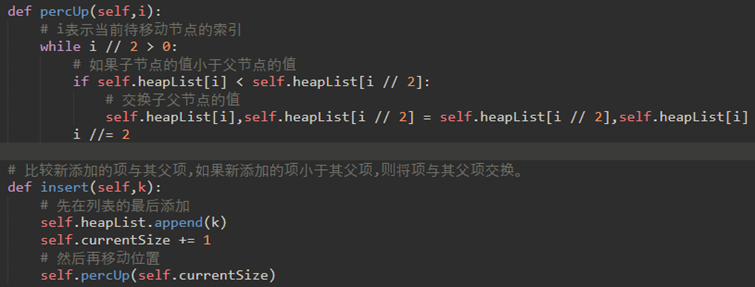
代码实现如下:
当然,如果使用递归的话,percUp可以改为:
\55. delMin弹出根节点很简单,难点在根被删除后恢复堆结构和堆顺序属性。
我们可以分两步恢复我们的堆:
a) 首先,将列表中的最后一个项移动到根位置来恢复根项,保持我们的堆结构属性。
b) 第二,我们通过将新的根节点沿着树向下推到其正确位置来恢复堆顺序属性。
(简单来说:将新的节点和其子节点重复交换,直到该节点小于两个子节点)
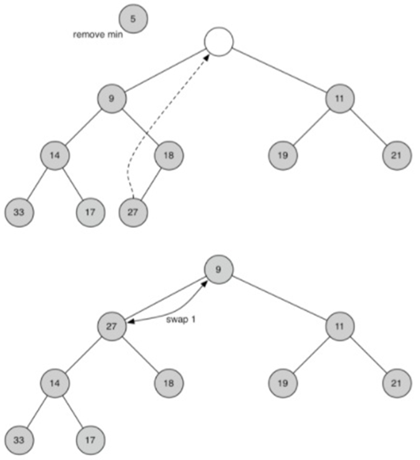
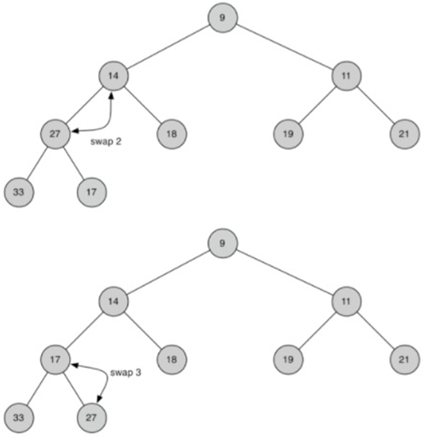
代码实现: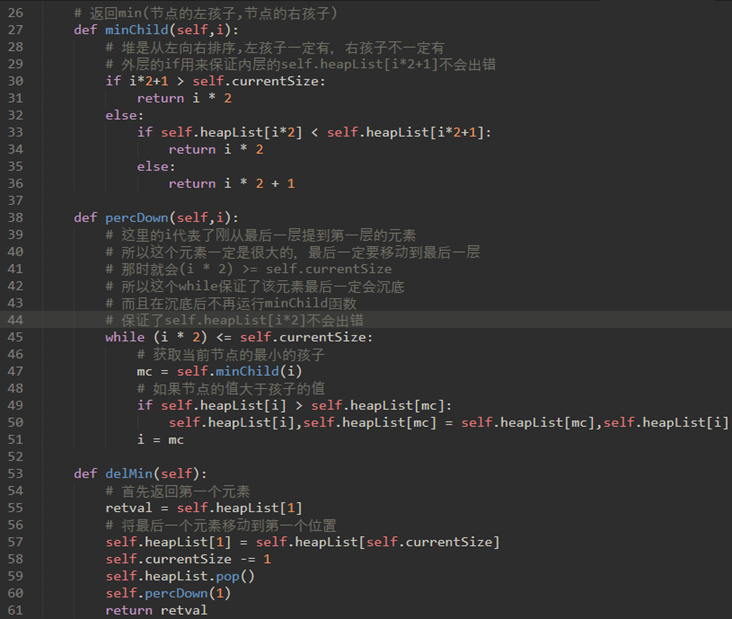
\56. 上面的代码是创建一个空的二叉堆,然后不断调用insert来创建堆,现在我们来看一下从一个列表构建整个堆的方法。
也就是实现buildHeap(list)方法。
对于一个排好序的列表,我们可以用二分搜索找到合适的位置,然后在下一个位置插入这个键值到堆中,时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动,为新节点腾出位置,时间复杂度为O(n)。因此用insert方法插入整个列表的的总开销是O(nlogn)。
其实我们能直接将整个列表生成堆,将总开销控制在O(n)。
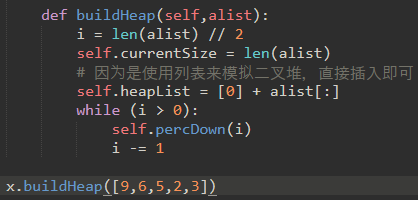
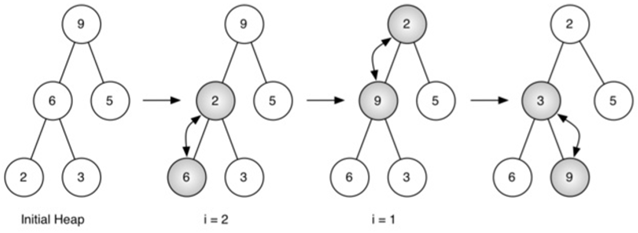
我们从树中间开始,然后回溯到根节点,但percDown方法保证了最大子节点总是“下沉”。
因为堆是一个完整的二叉树,超过中途点的任何节点都将是树叶,因此没有子节点。
\57. 二叉堆的完整代码实现:
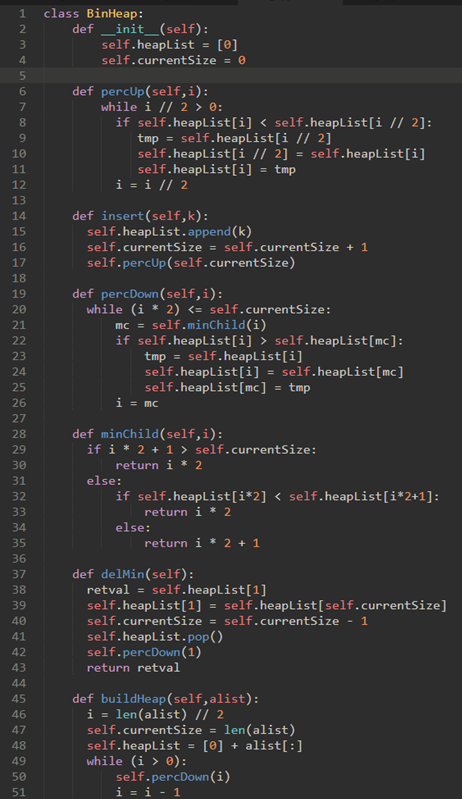
\58. 二叉树创建堆的复杂度:O(n)
二叉树堆排序的服制度:O(logN)
\59. 二叉查找树:
py里的map类型是一种映射类型,能从键映射到值。二叉查找树也可以做到类似于map一样的映射功能。
要实现映射类型,就需要知道映射类型的api:
a) Map()创建一个新的空map。
b) put(key,val)向map中添加一个新的键值对。如果键已经在map中,那么用新值替换旧值。
c) get(key)给定一个键,获取存储在map中的值,否则为None。
d) del使用del map[key]形式的语句从map中删除键值对。
e) len()返回存储在映射中的键值对的数量。
f) in如果给定的键在map中返回True。
\60. 查找树实现:
查找树是如何实现映射关系的?
二叉搜索树依赖于在左子树中找到的键小于父节点的属性,并且在右子树中找到的键大于父代。我们将这个称为bst属性。
说人话:对于二叉搜索树来说,左孩子的值小于父节点的值小于右孩子的值。
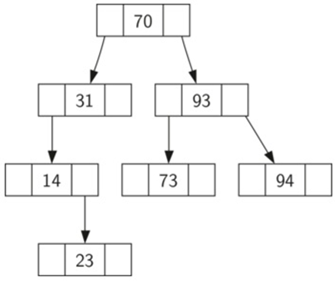
插入列表:70,31,93,94,14,23,73。
因为70是插入树中的第一个键,它是根。
接下来,31小于70,所以它成为70的左孩子。接下来,93大于70,所以它成为70的右孩子。现在我们有两层的树填充,下一个键94,因为94大于70和93,它成为93的右孩子。类似地,14小于70和31,所以它变成31的左孩子。23也小于31,所以它必须在左子树31中。但是,它大于14,所以它成为14的右孩子。
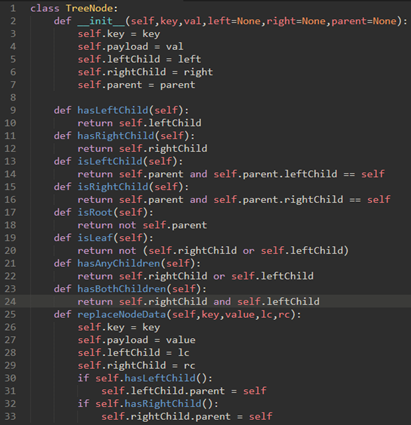
\61. 为了实现二叉搜索树,我们将使用类似于我们用于实现链表的节点和引用方法。
实现链表时定义了链表类(UnorderedList)和节点类(Node)。其中链表类引用了节点类,维护了头节点。
实现二叉搜索树时需要定义二叉搜索树类(BinarySearchTree)和节点类(TreeNode)。其中二叉搜索树类引用了节点类,维护了根节点。
\62. 代码实现:
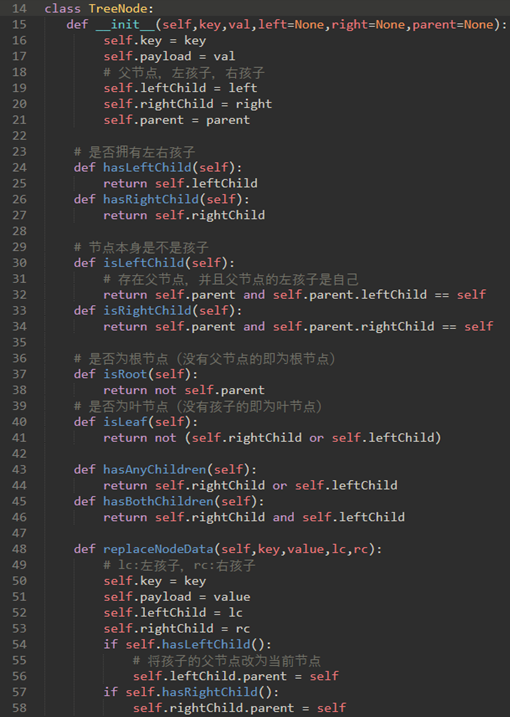
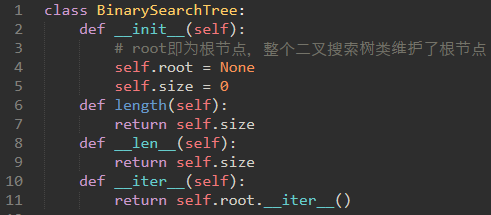
链表里的节点不仅存储了节点的值,还存储了下一个节点的引用;
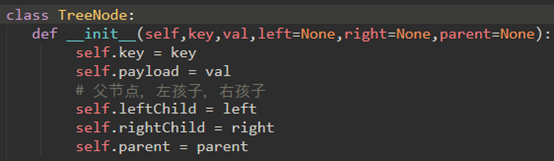
二叉搜索树的节点不仅存储了节点的键和值,还存储了左右孩子和父节点的引用。
\63. 现在可以对比散列表与二叉搜索树的区别:
散列表是使用列表slots和data来存储键和值的,然后使用散列函数来精确找到某个键对应的slots的索引值,接着将data列表里的值取出来
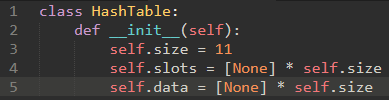
二叉搜索树是使用节点来存储键和值,然后使用树的查找性质来查找某个节点的。
\64. 定义BinarySearchTree类的put方法来构建二叉搜索树:
将检查树是否已具有根。如果没有根,那么put将创建一个新的TreeNode并将其做为树的根。如果根节点已经就位,则put调用私有递归辅助函数_put根据以下算法搜索树:
a) 从根节点开始,搜索二叉树,将新键与当前节点的键比较。若新键小于当前节点,则搜索左子树。若新键大于当前节点,则搜索右子树。
b) 当没有左(或右)孩子时,我们在树中找到应该建立新节点的位置。
c) 要向树中添加节点,请创建一个新的TreeNode对象,并将对象插入到上一步发现的节点。
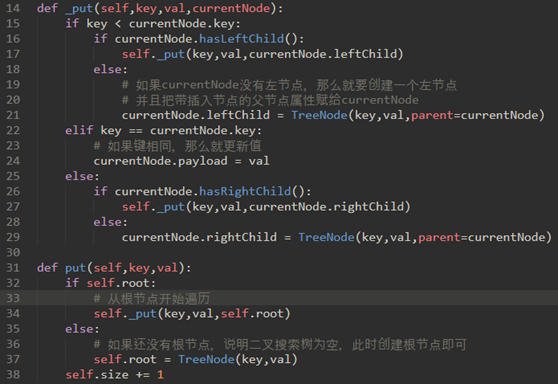
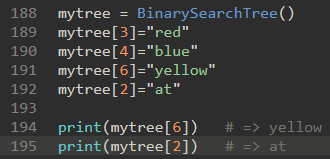
\65. 当put方法定义后,我们可以通过使用__setitem__方法调用put方法来重载[]运算符。
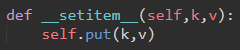
这样我们可以编写像myZipTree[‘Plymouth’]=55446这样的Python语句,就像Python字典一样。
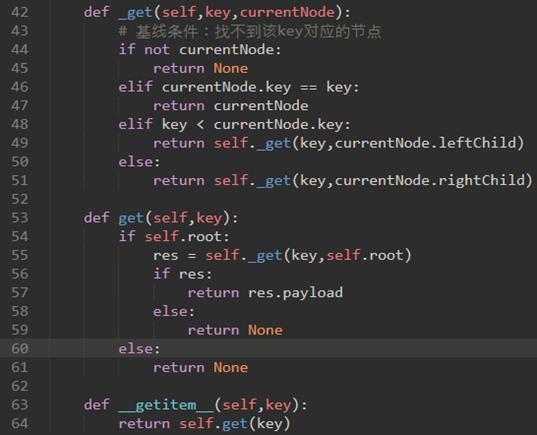
\66. get方法:
一旦树被构造,下一个任务是实现对给定键的值的检索。
递归地搜索树,直到它到达不匹配的叶节点或找到匹配的键。
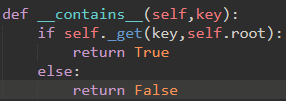
我们还可以重载in操作符:
\67. 二叉搜索树最难的操作:删除一个键。
第一个任务使用_get方法搜索以找到需要删除的TreeNode。如果未找到键,del操作符将引发错误
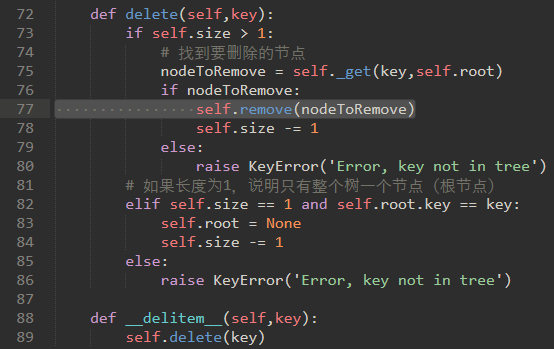
77行的remove方法尚未实现(后续补充)
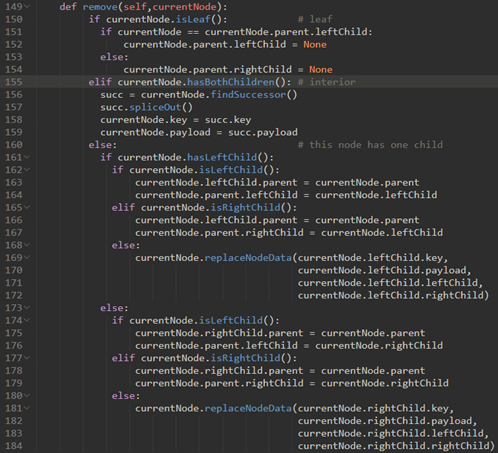
\68. 现在考虑remove方法:
若找到了待删除节点,必须考虑三种情况:
a) 待删除节点没有子节点(图一)
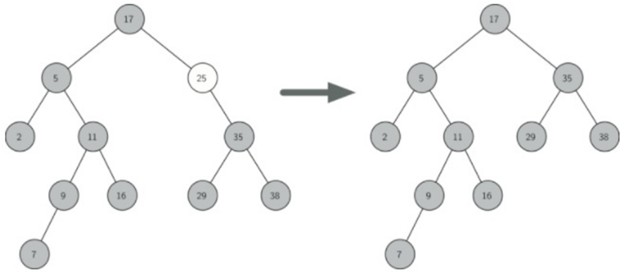
b) 待删除节点只有一个子节点(图二)
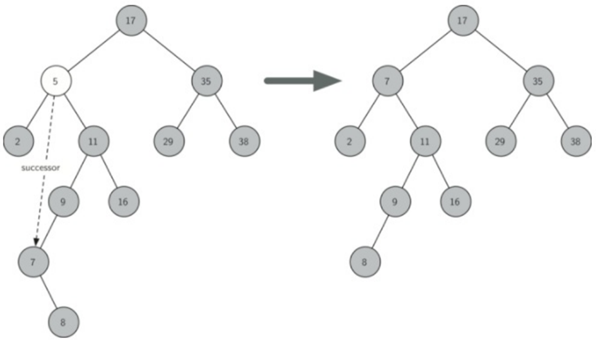
c) 待删除节点有两个子节点(图三)
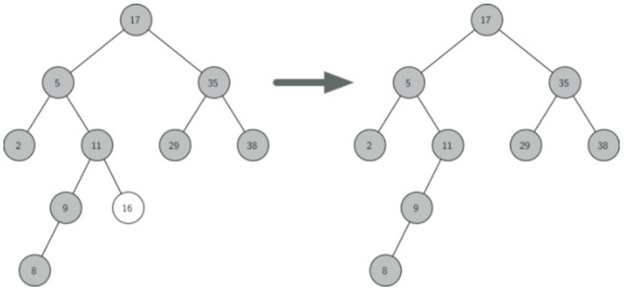
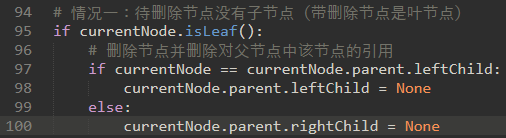
\69. 情况一:待删除节点是叶节点。
删除节点并删除对父节点中该节点的引用。
情况二:待删除节点有一个孩子。
孩子取代其父。
当前节点具有左孩子的情况。决策如下:
a) 如果当前节点是左子节点,则我们需要更新左子节点的父引用以指向当前节点的父节点,然后更新父节点的左子节点引用以指向当前节点的左子节点。
b) 如果当前节点是右子节点,则我们只需要更新右子节点的父引用以指向当前节点的父节点,然后更新父节点的右子节点引用以指向当前节点的左子节点。
c) 如果当前节点没有父级,则它是根。在这种情况下,我们将通过在根上调用replaceNodeData方法来替换key,payload,leftChild和rightChild数据。
节点具有右孩子的情况同理。
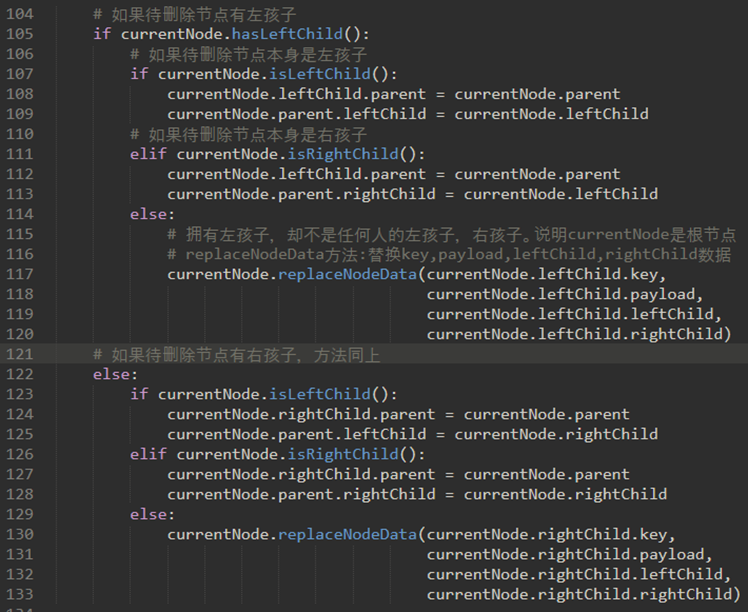

\70. 情况三:待删除节点有两个子节点。
是最难处理的情况。我们需要在树中搜索可用于替换被调度删除的节点的节点。
执行此操作的节点是树中具有次最大键的节点。我们将这个节点称为后继节点(Successor)。
后继结点:在二叉树中中序遍历的序列中,某个节点紧随的那个节点。
继承节点保证没有多于一个孩子。
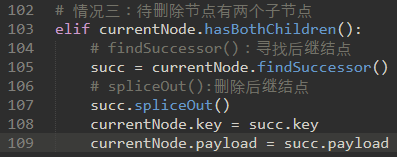
findSuccessor和spliceOut都是TreeNode类的方法。
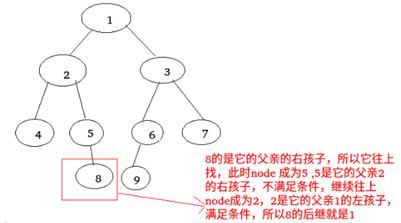
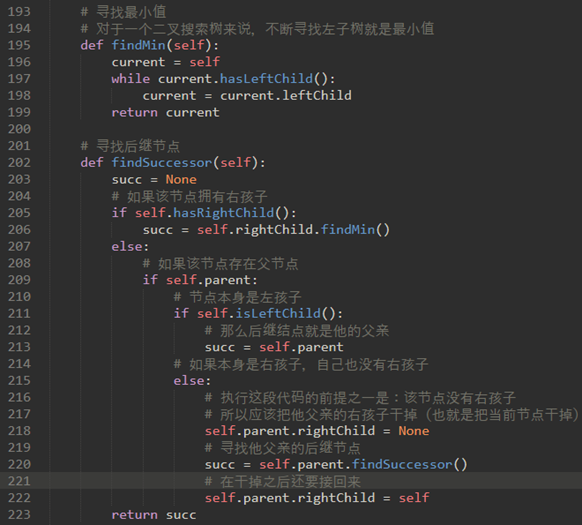
\71. findSuccessor:在二叉树中中序遍历的序列中,某个节点紧随的那个节点。在寻找接班人时,有三种情况需要考虑:
a) 如果节点有右子节点,则后继节点是右子树中的最小的键。
b) 如果节点没有右子节点并且是父节点的左子节点,则父节点是后继节点。
c) 如果节点是其父节点的右子节点,并且它本身没有右子节点,则此节点的后继节点是其父节点的后继节点,不包括此节点。
对于第三种情况:中序遍历:425819637
\72. spliceOut:删除后继结点。
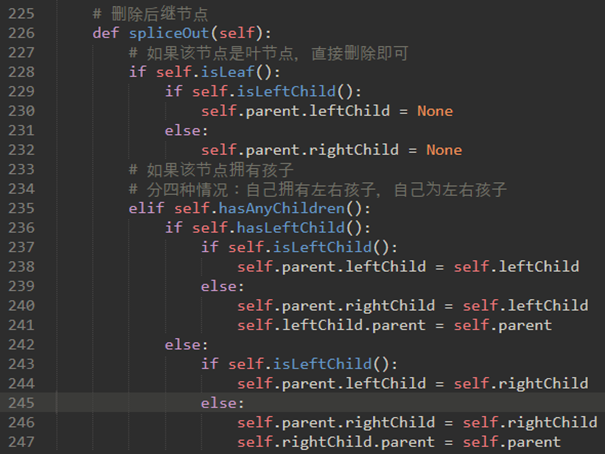
\73. 最后我们将二叉搜索树制作成迭代器:
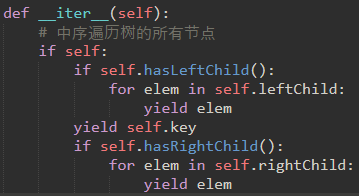
注意:__iter__覆盖for x in操作,因此它是递归的!
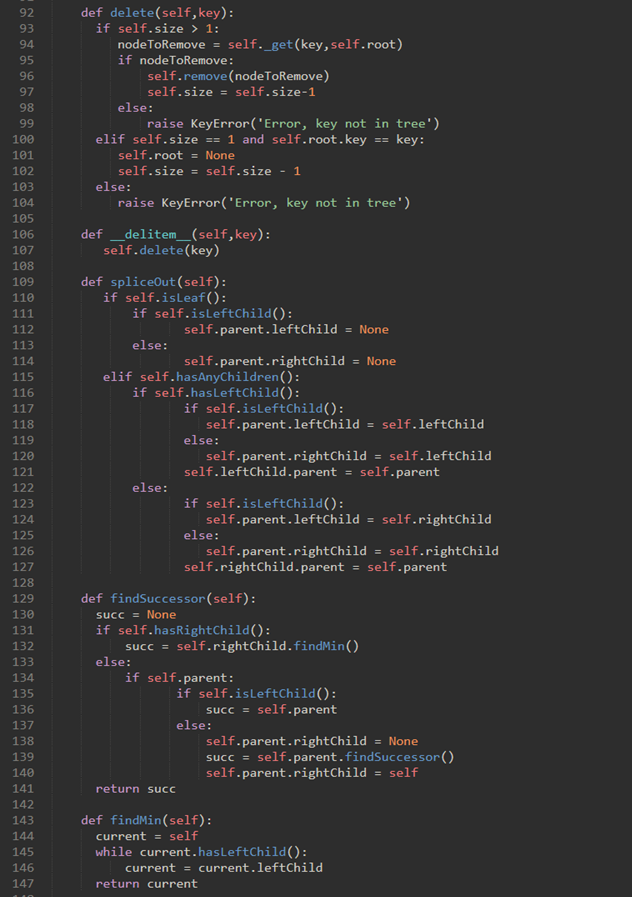
\74. 整个remove方法如下: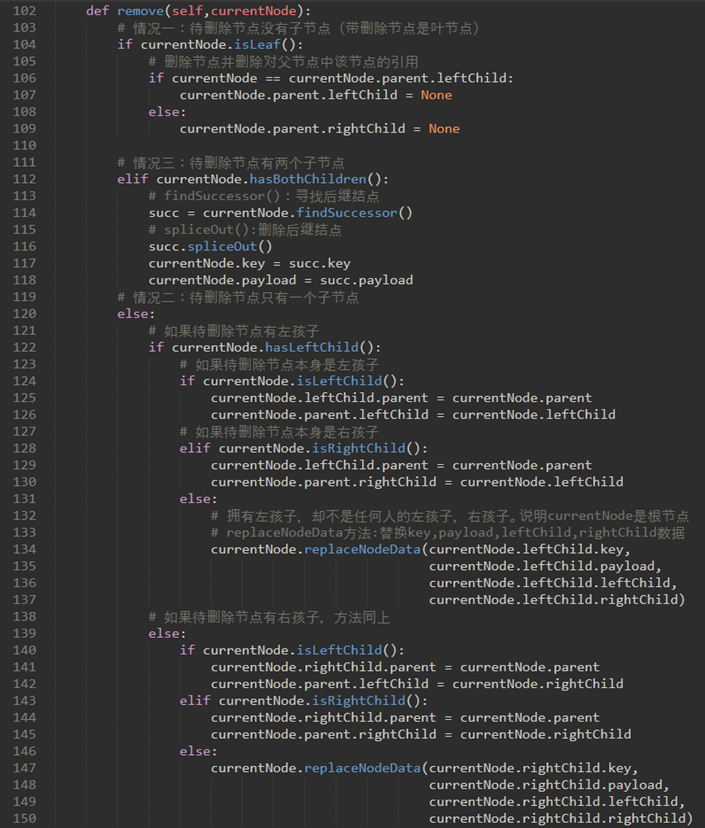
findsuccessor和spliceOut方法在上面。
\75. 所以,整个文件代码如下:
二叉树类如下:
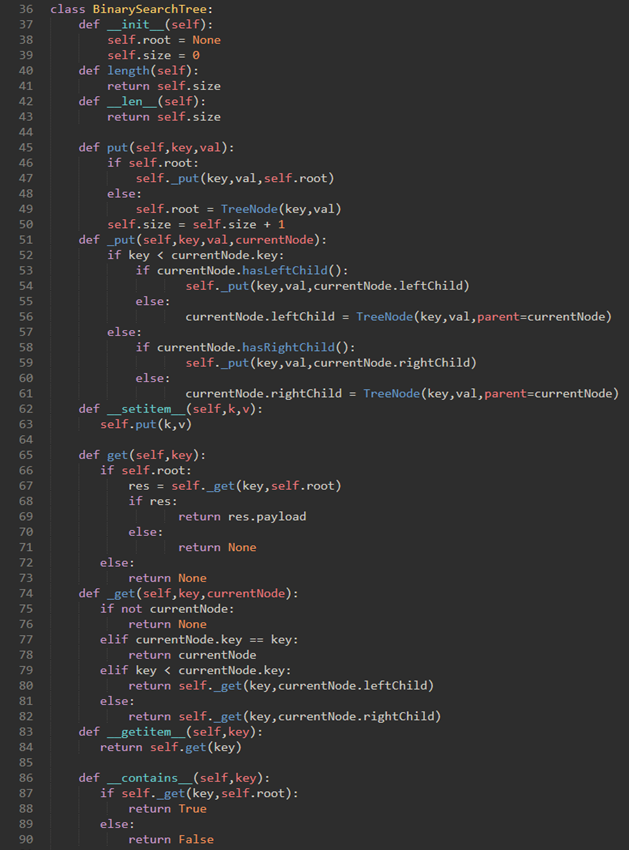
TreedNode类如下:
测试:
\76. 总结三种遍历:
a) 前序遍历:用于按顺序从前到后扫描整棵树。
b) 中序遍历:用于寻找二叉搜索树的后继结点。
c) 后续遍历:用于合并叶节点一直到根节点。
\77. 查找树分析:
对二叉搜索树各个方法进行分析:
put方法。其性能的限制因素是二叉树的高度。(树的高度指的是根到最深叶节点之间的边的数量)
如果按照随机顺序添加键,树的高度将在logN附近,其中n是树中的节点数。这是因为如果键是随机分布的,其中大约一半将小于根,一半大于根。
完全平衡的二叉树中的节点总数为2^(h+1)-1,其中h表示树的高度。
因为需要层层深入,所以在平衡二叉树中,put的最坏情况性能是O(logN),n是树中的节点数。
当然,如果树不平衡,put的复杂度将会是O(n):如下。
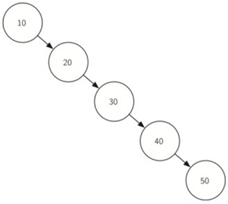
\78. get搜索树以找到键,在最坏的情况下,树被一直搜索到底部,并且没有找到键。
del最坏的情况也是深入到树的高度,但是比起get需要有一个加倍因子。
所以说:
a) 在平衡二叉树里,get,del,put的最坏情况性能是O(logN)。
b) 在不平衡的二叉树里,get,del,put的最坏情况性能是O(N)。
其中N是二叉树的节点数。
\79. 平衡二叉搜索树:
就像上面说的,如果二叉搜索树不平衡,二叉搜索树的性能可以降级到O(n)的操作。
为了实现更好的性能,现在我们使用一种特殊类型的二叉搜索树,它自动确保树始终保持平衡。这棵树被称为AVL树。
为了实现AVL树,我们通过查看每个节点的左右子树的高度,以此来跟踪树中每个节点的平衡因子
平衡因子就是:左子树的高度和右子树的高度之间的差。
balanceFactor=height(leftSubTree)-height(rightSubTree)根据公式:
a) 如果平衡因子大于零,则子树是左重的。
b) 如果平衡因子小于零,则子树是右重的。
c) 如果平衡因子是零,那么树是完美的平衡。
注意:平衡因子是节点的属性,而不是树的属性。也就是说,每个节点都有自己的平衡因子。
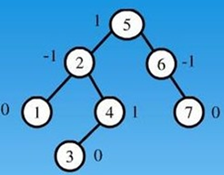
5的结点平衡因子就是3-2=1;
2的结点平衡因子就是1-2=-1;
4的结点平衡因子就是1-0=1;
6的结点平衡因子就是0-1=-1;
叶子结点都是为0;
节点不一定能全部填满最底层,这时平衡因子是1或-1.
所以若平衡因子是-1,0或1,我们定义树平衡。
所以说,一旦AVL树的平衡因子不为-1,0,1我们就需要实现一个程序让其自动恢复平衡。
\80. AVL平衡二叉搜索树:
考虑最极端的情况:一棵树最不平衡的情况。
下面是虑高度为0,1,2,3最不平衡的树:
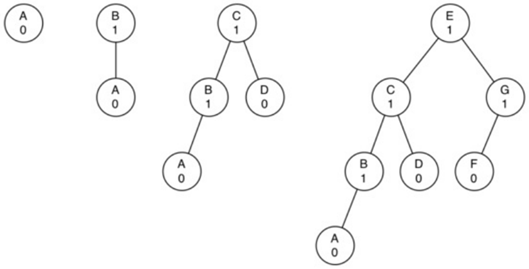
对于高度为0的树,有1个节点,
对于高度为1的树,有1+1=2个节点,
对于高度为2的树,有1+1+2=4个节点,
对于高度为3的树,有1+2+4=7个节点。
总结出公式:
高度h(Nh)的树中的节点数量:
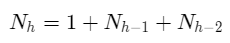
它非常类似于斐波纳契序列。
第i个斐波纳契数字Fi为:
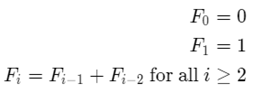
随着斐波纳契数列越来越大,Fi/Fi-1的比率越来越接近黄金比率Φ=(1+√5)/2。
我们将简单地使用该方程来近似Fi,如Fi=Φ^i/5。如果我们利用这个近似,我们可以重写Nh的方程为:
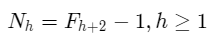
通过用其黄金比例近似替换斐波那契参考,得到
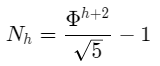
如果我们重新排列这些项,并取两边的底数为2的对数,然后求解h,我们得到以下推导:
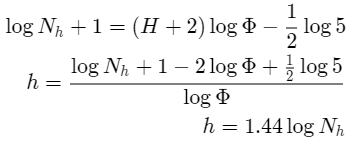
这个推导告诉我们,在任何时候,AVL树的高度等于树中节点数目的对数的常数(1.44)倍。
这是搜索我们的AVL树的好消息,因为它将搜索限制为O(logN)。
\81. AVL平衡二叉搜索树实现:
一旦添加新叶,我们必须更新其父的平衡因子:
a) 如果新节点是右子节点,则父节点的平衡因子将减少1。
b) 如果新节点是左子节点,则父节点的平衡因子将增加1。
这个关系需要递归地应用到新节点的祖父节点,这时又有两种情况:
c) 一直递归调用到达树的根。
d) 父节点的平衡因子已调整为零。
(也就是说,一旦一个子树的平衡因子为零,那么它的祖先节点的平衡不会改变)
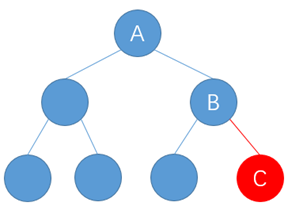
C为新插入的节点。
在插入之前,
节点A的平衡因子为2-2=0。
节点B的平衡因子为1-0=1。
在插入C后,
B的平衡因子为1-1=0。
也就是说,此时C的父节点B的平衡因子已经调节为0,此时不会再影响祖先节点A的平衡因子。
\82. 上面的思路转为代码如下:
注意_put方法和前面二叉搜索树的_put一样,不过添加了25和31行两个updateBalance方法。
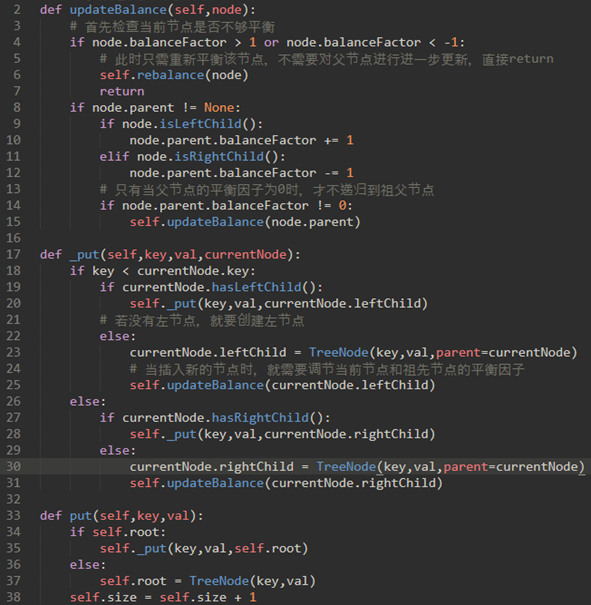
注意15行递归调用了updateBalance方法。
也就是说,在递归调节祖先节点的平衡因子的过程中,某个节点的平衡因子的绝对值可能就超过了1。这时候就需要对整棵树进行调整。调整使用reblance方法。
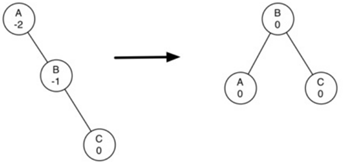
上面左图,一开始树只有AB节点,然后插入C节点。
在尚未插入C节点的情况下,树是平衡的。在插入C节点后,首先调节节点B的平衡因子为-1,然后递归调节节点A的平衡因子为-2。此时A的平衡因子过大,这是就需要使用reblance方法:
为了使AVL树恢复平衡,我们将在树上执行一个或多个旋转。
对于上面的情况,我们以节点A为根的子树的左旋转:
a) 提升右孩子(B)成为子树的根。
b) 将旧根(A)移动为新根的左子节点。
c) 如果新根(B)已经有一个左孩子,那么使它成为新左孩子(A)的右孩子。
(由于新根(B)是A的右孩子,所以旋转后的A肯定没有右孩子的。这允许我们添加一个新的节点作为右孩子,不需进一步的考虑)
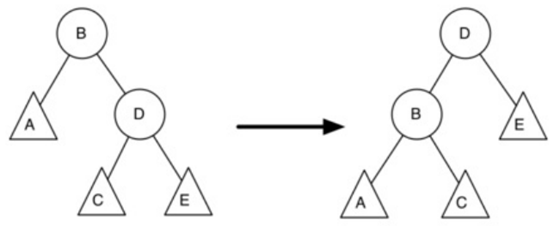
\83. 让我们再看一个更加复杂的旋转:
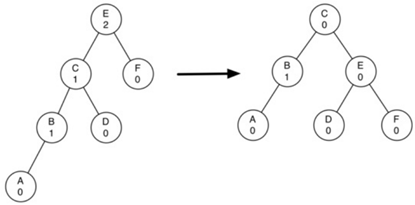
左图树的根的平衡因子为2,要执行右旋转:
a) 提升左子节点(C)为子树的根。
b) 将旧根(E)移动为新根的右子树。
c) 如果新根(C)已经有一个正确的孩子(D),那么使它成为新的右孩子(E)的左孩子。
(由于新根(C)是E的左子节点,因此E的左子节点在此时保证为空。这允许我们添加一个新节点作为左孩子,不需进一步的考虑)
已知:
a) newBal(B)=hA−hC
b) oldBal(B)=hA−hD
c) oldBal(B)=hA−(1+max(hC,hE))
三个方程合并计算:
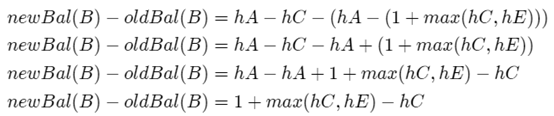
将oldBal(B)移动到方程的右边,并利用
max(a,b)-c=max(a-c,b-c)。得到:
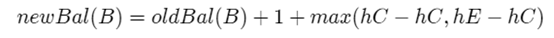
但是,hE-hC与-oldBal(D)相同。因此,我们可以使用另一个表示max(-a,-b)=-min(a,b)的标识
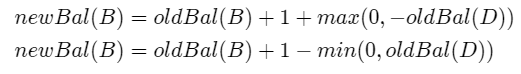
上面的公式就是第16行代码。
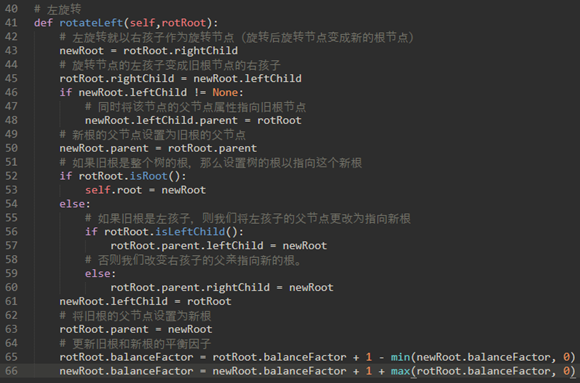
\84. 现在我们已经能写成左右旋转的代码了,那么如何使用左右旋转的代码?
左图,由于节点A的平衡因子为-2,我们应该做左旋转。当我们围绕A做左旋转,变成右图。
如果我们再做右旋以纠正,就又回到左图。
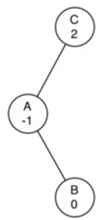
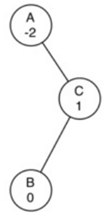 →
→ 
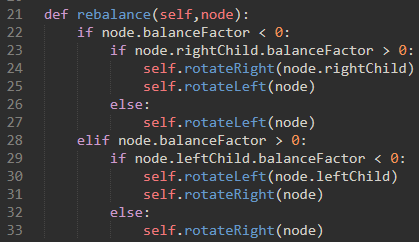
要纠正这个问题,我们必须使用以下规则集:
a) 如果子树需要左旋转使其平衡,首先检查右子节点的平衡因子。如果右孩子是重的,那么对右孩子做右旋转,然后是原来的左旋转。
b) 如果子树需要右旋转使其平衡,首先检查左子节点的平衡因子。如果左孩子是重的,那么对左孩子做左旋转,然后是原来的右旋转。
所以,上面情况正确的做法是:
从围绕节点C的右旋转开始,将树放置在A的左旋转使整个子树恢复平衡的位置。
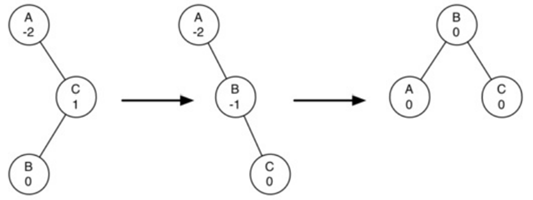
上面的规则就可以使用下面的代码:
\85. 通过保持树的平衡,我们可以确保get方法将按O(logN)时间运行。
但问题是我们的put方法有什么成本?
由于将新节点作为叶子插入,更新所有父节点的平衡因子将需要最多logN运算,树的每层一个运算。如果发现子树不平衡,则需要最多两次旋转才能使树重新平衡。但是,每个旋转在O(1)时间中工作,因此我们的put操作仍然是O(logN)。
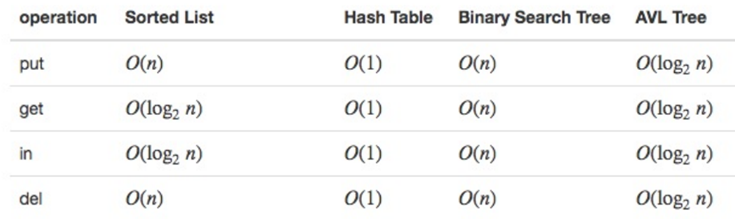
\86. Map抽象数据结构总结:
在前面两章中,我们已经研究了可以用于实现Map抽象数据类型的几个数据结构:
二叉搜索表,散列表,二叉搜索树和平衡二叉搜索树。
总结这一节,让我们总结Map ADT定义的关键操作的每个数据结构的性能
AVL树部分跳过了:195-197页。